Inverse Geometric Transformations

An inverse geometric transformation is the process that reverses the effects of an initial geometric transformation.

In other words, the inverse transformation is what brings a shape or object back to its original state when applied after the initial transformation.

Just like the original, the inverse is still considered a geometric transformation.

Note: Mathematically, if a transformation is represented by a matrix A, its inverse is represented by the inverse matrix A^-1, such that multiplying matrix A by A^-1 yields the identity matrix $$ A \cdot A^{-1} = I $$. This means that applying A followed by A^-1 leaves the object unchanged, and the same concept applies in geometry.

A Practical Example

Let's consider a geometric shape on a plane.

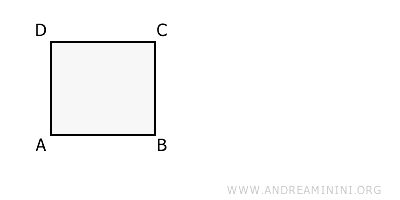
Now, let's apply a translation T that moves the shape 5 centimeters to the right.

This translation is a geometric transformation.

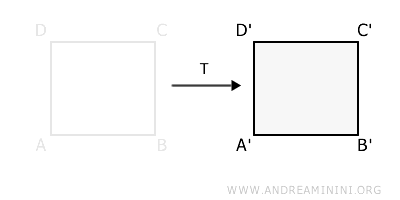
The inverse of this transformation is a translation T^-1 that moves the shape 5 centimeters to the left.

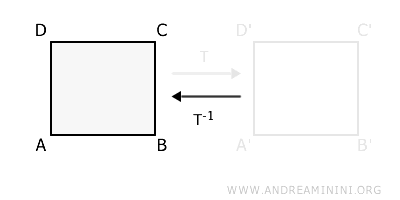
Essentially, the inverse transformation undoes the effect of the original transformation.

Combining the geometric transformation T with its inverse T^-1 results in the identity I.

$$ T \circ T^{-1} = I $$

Example 2

Let's use the same shape from the previous example.

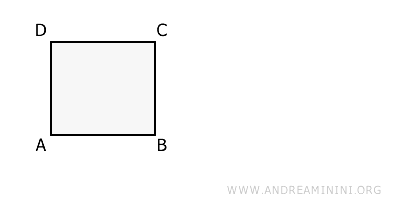
This time, let's apply a rotation R of 45° clockwise, using point A as the center.

Rotation, like translation, is a geometric transformation.

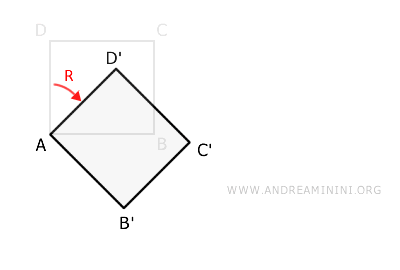
The inverse of this transformation R^-1 is a 45° counterclockwise rotation.

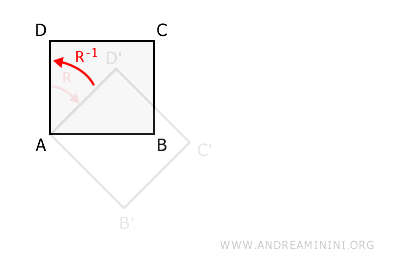
Once again, the inverse transformation cancels out the effect of the initial transformation.

Combining the geometric transformation R with its inverse R^-1 results in the identity I.

$$ R \circ R^{-1} = I $$

And so on.