Translation
Translation is a geometric transformation (isometry) that shifts every point in a figure by the same distance and in the same direction, along a specified line.
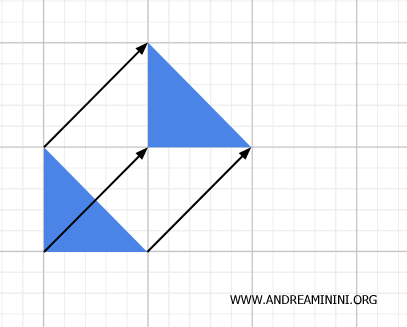
This movement is represented by vectors known as "translation vectors." The length, or magnitude, of these vectors corresponds to the distance traveled during the translation.
The direction of the vector shows the path of the movement, while the arrowhead indicates its orientation.
Direction and orientation are two distinct concepts. Direction refers to the line along which the movement occurs (e.g., horizontal, vertical, diagonal, etc.), while orientation specifies which way along that line the movement is going. For instance, an object moving horizontally can go either left or right. The direction is the horizontal line, and the orientation tells us whether it’s moving left or right.
In geometry, a translation on a plane is represented by a pair of numbers (x;y):
- The first value, "x," denotes horizontal movement. By convention, a positive value indicates movement to the right, while a negative value indicates movement to the left.
- The second value, "y," specifies vertical movement. A positive value indicates upward movement, and a negative value indicates downward movement.
In other words, the two numbers in the pair represent the movement of an object along the horizontal (x) and vertical (y) axes.
The x and y values are the components of the movement.
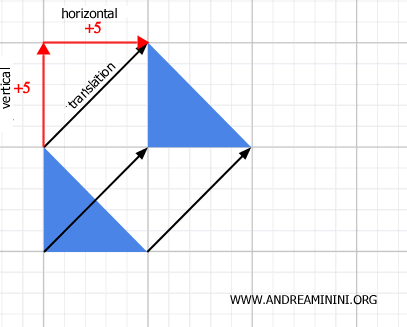
When a geometric figure is translated, it remains congruent to the original because its shape and size do not change.
After translation, the distance between any two points on the figure remains the same.
Thus, translation is a specific type of isometry.
Note. A translation can also be described as a geometric transformation that assigns to each point \( P \) in the plane a corresponding point \( P' \), such that the vector \( \vec{PP'} \) is equal to a fixed translation vector \( \vec{v} \); in other words, \( \vec{PP'} = \vec{v} \).
Translation Equations
The equations that describe a translation are expressed in terms of the x and y components of the movement.
$$ \begin{cases} x' = x_0 + x \\ \\ y' = y_0 + y \end{cases} $$
Here, x' and y' represent the new coordinates, while x and y indicate the displacement relative to the original coordinates x0 and y0.
Example
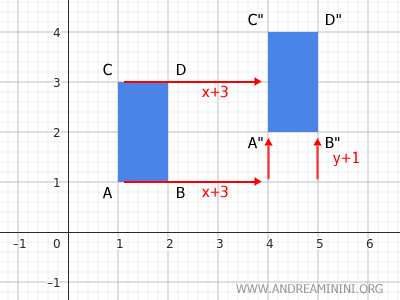
The rectangle ABCD has its vertices at coordinates A(1;1), B(2;1), C(1;3), and D(2;3) on the plane.
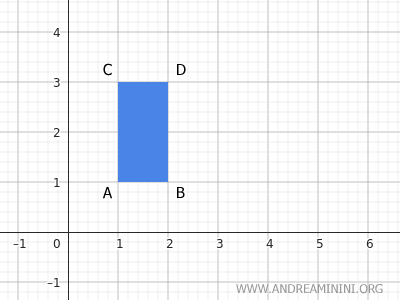
Now, consider a translation (3;1), which moves the figure 3 units to the right horizontally (x=3) and 1 unit up vertically (y=1).
Apply the horizontal translation of +3 to the x-coordinate of each point in the figure:
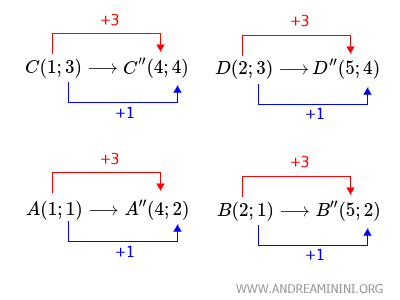
$$ \begin{cases} A'(1+3;1) \\ B'(2+3;3) \\ C'(1+3;3) \\ D'(2+3;3) \end{cases} $$
$$ \begin{cases} A'(4;1) \\ B'(5;2) \\ C'(4;1) \\ D(5;2) \end{cases} $$
This shifts the entire figure to the right.
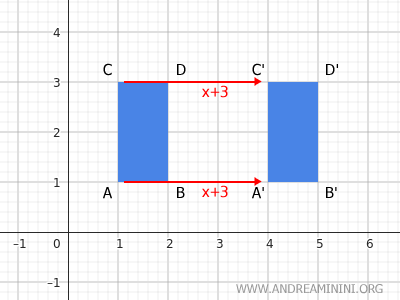
The red arrows represent the displacement vectors for the x (horizontal) component.
Each point of the figure is shifted horizontally by the same amount. In this case, each point moves 3 units to the right.
What is a vector? A vector is a quantity characterized by a magnitude, known as its modulus, a direction, and an orientation. The tail of the vector marks the starting point, while the arrowhead marks the endpoint.

For example, a vector that originates at point A and ends at point A' is called a "vector applied at point A." In the case of translation, the same vector is applied to every point in the geometric figure.
Next, I apply the vertical translation of +1, shifting points A', B', C', and D' of the figure upward.
$$ \begin{cases} A'(4;1+1) \\ B'(5;2+1) \\ C'(4;1+1) \\ D(5;2+1) \end{cases} $$
$$ \begin{cases} A'(4;2) \\ B'(5;3) \\ C'(4;2) \\ D(5;3) \end{cases} $$
These are the final coordinates of the figure after the translation.
In other words, I have algebraically added the components (x;y) of the vector v(3;1) to the coordinates (x;y) of each point in the figure.
Translating a Function
Translating a function \( y = f(x) \) involves shifting every point on its graph by a vector \( \vec{v} = (a, b) \), without altering the shape of the curve. The resulting function is: $$ y' = f(x' - a) + b $$
Given an original function \( y = f(x) \), applying a translation means adjusting the coordinates of all its points using the vector \( \vec{v} = (a, b) \): $$ \begin{cases} x' = x + a \\ y' = y + b \end{cases} $$
To express the translated function in terms of the new coordinates, we rewrite the original variables as:
$$ \begin{cases} x = x' - a \\ y = y' - b \end{cases} $$
Substituting into the original equation \( y = f(x) \), we get:
$$ y' - b = f(x' - a) $$
$$ y' = f(x' - a) + b $$
This is the general form of the translated function.
The graph of the function is shifted by \( a \) units horizontally (along the x-axis) and \( b \) units vertically (along the y-axis).
Special Cases
Two notable cases arise when the translation occurs along a single axis:
- Vertical translation (along the y-axis)
Setting \( a = 0 \) yields a purely vertical shift: $$ y' = f(x) + b $$ - Horizontal translation (along the x-axis)
Setting \( b = 0 \) gives a purely horizontal shift: $$ y' = f(x - a) $$
Example
Consider the quadratic function:
$$ y = 3x^2 $$
We want to translate it by the vector \( \vec{v} = (4, 5) \), meaning 4 units to the right and 5 units up.
Substituting into the general translation formula gives:
$$ y = 3(x - 4)^2 + 5 $$
This new equation describes the same parabola, now relocated in the Cartesian plane.
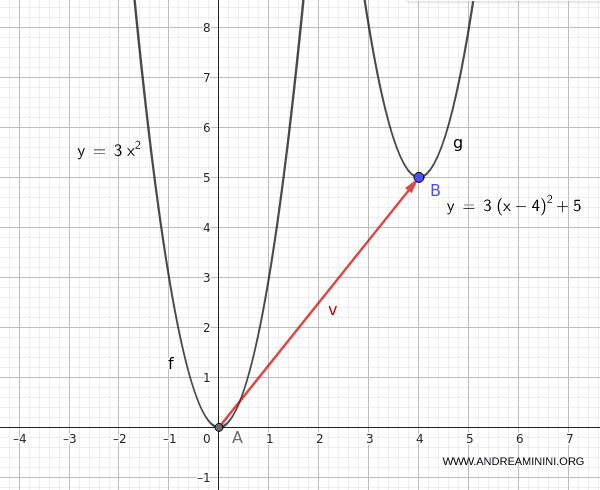
Note. This kind of transformation is particularly helpful when analyzing how the position of a graph changes without affecting its shape. In essence, the function’s "identity" remains unchanged - only its location is modified.
Translation as an Isometry
Translation is an isometry because the relative distance between points does not change after the geometric transformation.
Proof
To prove that a translation is an isometry, consider any two points A and B on a figure.
Apply the same translation vector $ \vec{v} $$ to these two points, and identify the new positions of points A' and B' after the geometric transformation.
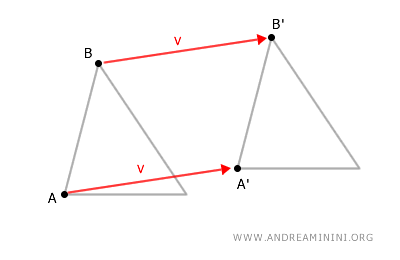
In an isometry, the distance between points does not change.
So, we need to prove that the distance between points A' and B' is the same as the distance between points A and B.
The segments AA' and BB' are congruent and parallel because the same translation vector was applied to both.
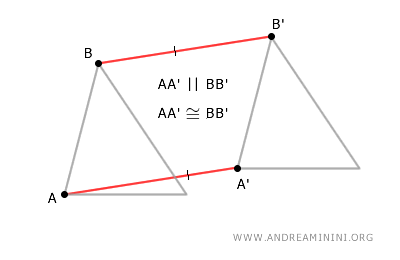
Therefore, when connecting all the points, the figure AA'B'B forms a parallelogram.
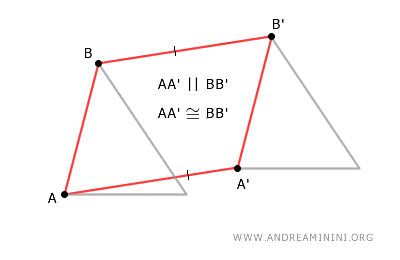
In a parallelogram, all opposite sides are congruent and parallel.
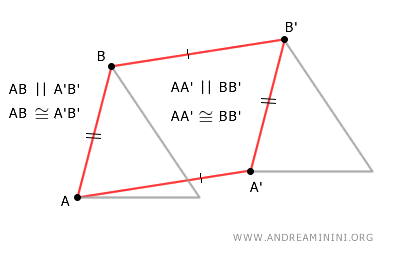
As a result, the segments AB and A'B' are also congruent, meaning they have the same length.
$$ \overline{AB} \cong \overline{A' B'} $$
This proves that the distance between points A and B is the same as the distance between points A' and B'.
Therefore, translation is an isometry.
Translation in Three-Dimensional Space
A translation in space is a geometric transformation that shifts every point of a solid object by a vector \(\vec{v}\), while preserving distances and angles between points.
If a point \( P(x, y, z) \) is translated by a vector \( \vec{v} = (a, b, c) \), its new coordinates after the transformation are:
\[ P'(x', y', z') = (x + a, y + b, z + c). \]
This illustrates that translation in three-dimensional space is simply vector addition applied to all three coordinates.
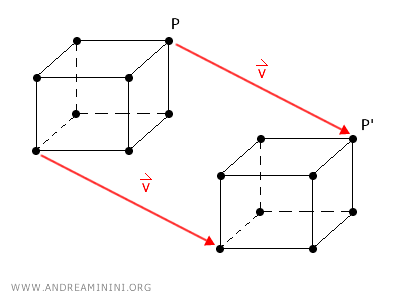
In three dimensions, translation follows the same principles as in two dimensions, with the only difference being the inclusion of a third coordinate.
Key Properties of Translation in Space
Translation preserves all the geometric properties of a solid figure, ensuring that the translated figure is perfectly congruent to the original.
Specifically, it maintains segment lengths, angle measures, parallel relationships, and collinearity.
As a result, translation in space is classified as an isometry, meaning it preserves distances between points.
Additionally, it is an affine transformation because it maintains parallelism, collinearity, and proportional relationships between aligned segments.
Notes
Here are some additional notes and observations about translation:
- The composition of multiple translations is still a translation
The sequential composition of two or more translations is equivalent to a single translation, with the resulting vector being the vector sum of the original translation vectors. So, performing two or more translations in succession on a figure is the same as applying a single translation defined by the combined vectors of the initial translations.
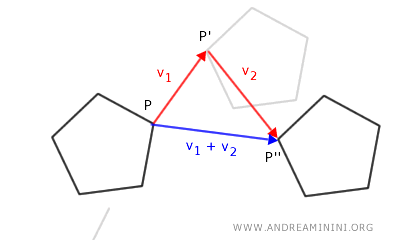
In analytic geometry, composing two translations defined by vectors \( \vec{v}_1 \) and \( \vec{v}_2 \) results in another translation, whose vector is given by \( \vec{v}_1 + \vec{v}_2 \).
- Commutative property
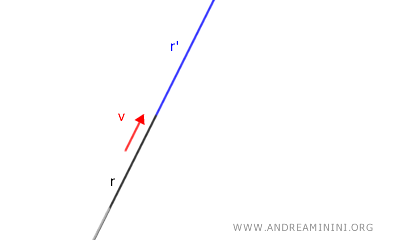
The composition of two translations with vectors \( \vec{v}_1 \) and \( \vec{v}_2 \) is commutative, meaning \( \vec{v}_1 \circ \vec{v}_2 = \vec{v}_2 \circ \vec{v}_1 \). - The translation of a line is always a parallel or coincident line.
If the translation vector has the same direction as the line, regardless of the orientation, the result is a coincident line.
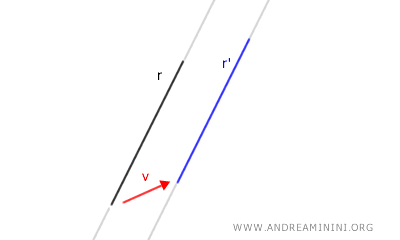
However, if the vector has a different direction, the result is a parallel line.
- A null translation is the same as the identity transformation
A translation is considered null if the translation vector is a zero vector, meaning a vector with a magnitude of zero and undefined direction and orientation.$$ \vec{v} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$ Adding the zero vector to any point results in the point remaining unchanged. Its Cartesian coordinates do not change. $$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$ Therefore, a null translation leaves a figure unchanged. The result is the same figure, also known as a identity transformation.What is an invariant figure? A figure is called an invariant figure if its transformed version is identical to the original figure. For example, a null translation results in an identity figure.
- Horizontal and Vertical Translations
Horizontal and vertical translations are specific cases of linear translations. When the translation vector is \( \vec{v}(a, 0) \), the transformation shifts all points horizontally; when it is \( \vec{v}(0, b) \), the shift is vertical. - Fixed Points
Any translation other than the identity has no fixed points.Note. A translation acts as the identity transformation only when both components of the translation vector are zero: \( \vec{v}(0, 0) \). If at least one component of the vector \( \vec{v}(a, b) \) is nonzero, then every point in the plane is displaced according to the rule: $$ \begin{cases} x' = x + a \\ \\ y' = y + b \end{cases} $$ As a result, no point can remain fixed under such a transformation.
- Lines parallel to the translation vector are invariant as a whole
Under a translation, any line parallel to the translation vector is carried onto itself: the isometry preserves the line as a set, even though its individual points are displaced.

And so on.
