Geometric Transformations
A geometric transformation is a one-to-one correspondence that pairs each point in a plane (or in space) with exactly one other point in the same plane (or space).
There are various types of geometric transformations, including rotations, translations, isometries, and more.
More formally, a geometric transformation is any invertible function T that maps each point P in a non-empty set X to a point P′ in the set Y.
$$ T: X \rightarrow Y $$
In this context, the set Y represents the image T(X) of the set X under the transformation T.

The point P′ in Y is known as the image or transform of P, while the point P in X is referred to as the preimage or inverse transform.
In simple terms, geometric transformations are mathematical operations that alter the position or shape of an object within a geometric space. These transformations can be applied to different geometric elements, such as points, lines, shapes, and solid figures.
Because the transformation is one-to-one, there also exists an inverse transformation $ T^{-1}: Y \rightarrow X $, which maps each point in set Y back to a corresponding point in set X.

The geometric properties that remain unchanged after a transformation are called invariants.
An Example
Let's consider a geometric figure ABC.
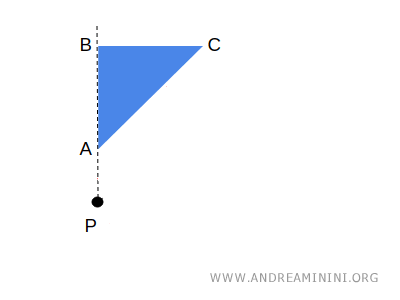
If I rotate a geometric figure by a certain angle alpha, I get a one-to-one correspondence between points A and A', B and B', C and C'.
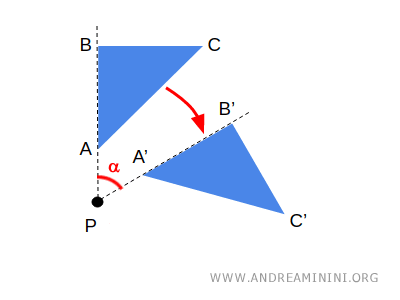
The points A', B', and C' after the transformation are called images or transformed points of points A, B, and C, respectively.
Considering the rotation as a bijective function f, we can also write:
$$ A' = f(A) $$
$$ B' = f(B) $$
$$ C' = f(C) $$
This notation reads as "A' is equal to f of A", and so on.
And of course, the same applies to all other points and segments of the figure.
For example, the segment A'B' is the image of segment AB.
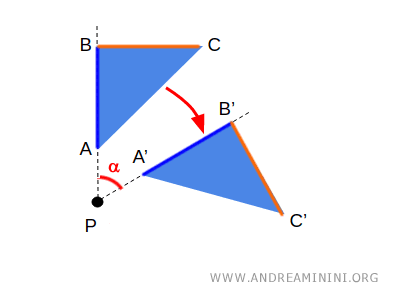
This is a practical example of a geometric transformation.
Note. In this example, point P has an image that corresponds to itself. In other words, point P does not change its position in the plane after the rotation. In this case, P is called a fixed point.
Types of Geometric Transformations
There are several types of geometric transformations.
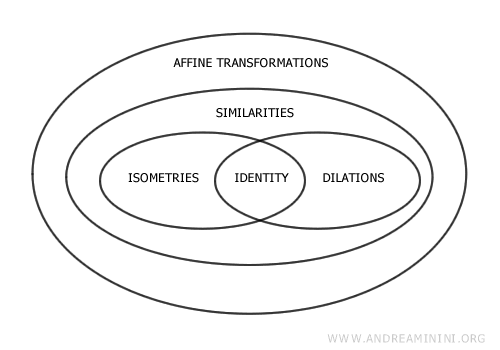
Here is a list of the main geometric transformations:
- Translation
Moving all points of a figure a constant distance in a specified direction. The translated figure retains the same shape and size as the original.
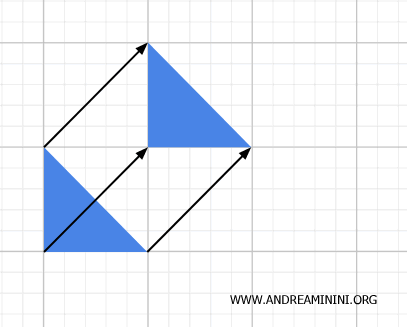
- Rotation
Circular movement of a figure around a fixed point (the center of rotation). The distance of each point in the figure from the center of rotation remains constant.
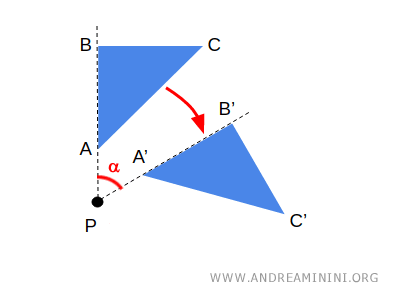
- Reflection (or Mirroring)
Flipping a figure across a line (the axis of reflection), creating a mirror image.
- Isometry
Isometries are geometric transformations that preserve distances between points and the dimensions of objects. For example, translation, rotation, and reflection are isometric transformations. - Homothety (Dilation or Scaling)
This transformation does not preserve dimensions but maintains the proportions and overall shapes of objects. It changes the size of a figure by multiplying the distances of all its points from a fixed point (the center of dilation) by a constant factor.
Geometric Transformations in Analytic Geometry
A geometric transformation can be expressed as a system of linear equations that yields exactly one solution for each coordinate pair: $$ \begin{cases} x' = ax + by + c \\ y' = dx + ey + f \end{cases} $$ Here, $x$ and $y$ are the original coordinates, $x'$ and $y'$ are the transformed coordinates, and $a, b, c, d, e, f$ are the transformation coefficients.
Put simply, each point $(x, y)$ maps to one and only one image $(x', y')$, and every $(x', y')$ has a unique pre-image $(x, y)$.
This one-to-one correspondence holds only when the system has a unique solution - that is, when the determinant is non-zero.
$$ \Delta = \begin{vmatrix} a & b \\ d & e \end{vmatrix} = ae - bd \neq 0 $$
Why must the system be linear? Linear transformations ensure continuity (no sudden jumps) and bijectivity (each point maps uniquely and reversibly). A non-zero determinant guarantees that the transformation is both invertible and well-defined across the entire plane or space.
Example
Consider the system:
$$ \begin{cases} x' = 2x - 3y + 5 \\ y' = x + 4y - 2 \end{cases} $$
This is an affine transformation, as it includes constant terms (5 and -2) added to the linear expressions.
We can rewrite it in a more compact form:
$$ \begin{cases} 2x - 3y = x' - 5 \\ x + 4y = y' + 2 \end{cases} $$
The coefficient matrix is:
$$\begin{pmatrix} 2 & -3 \\ 1 & 4 \end{pmatrix}$$
Now let’s compute the determinant to confirm the system has a unique solution:
$$ \Delta = \begin{vmatrix} 2 & -3 \\ 1 & 4 \end{vmatrix} = 2 \cdot 4 - (-3) \cdot 1 = 8 + 3 = 11 \ne 0 $$
Since the determinant is non-zero, the transformation is both invertible and bijective - meaning it qualifies as a proper geometric transformation.
This implies that every point has a unique image and a unique pre-image.
Example. Let’s apply the transformation to point $A(1, 2)$: $$ \begin{cases} x' = 2 \cdot 1 - 3 \cdot 2 + 5 = 2 - 6 + 5 = 1 \\ y' = 1 + 4 \cdot 2 - 2 = 1 + 8 - 2 = 7 \end{cases} $$ So $A(1, 2) \mapsto A'(1, 7)$ 
Now take $B(5, -1)$: $$ \begin{cases} x' = 2 \cdot 5 - 3 \cdot (-1) + 5 = 10 + 3 + 5 = 18 \\ y' = 5 + 4 \cdot (-1) - 2 = 5 - 4 - 2 = -1 \end{cases} $$ So $B(5, -1) \mapsto B'(18, -1)$
To find the inverse transformation, i.e. to recover $x$ and $y$ from $x'$ and $y'$, we can use either Cramer’s Rule or the inverse matrix method.
Let’s rewrite the system:
$$ \begin{cases} 2x - 3y = x' - 5 \\ x + 4y = y' + 2 \end{cases} $$
We’ll use Cramer’s Rule here, knowing that $ \Delta = 11 $.
Replace the first column with constants to find $ \Delta_x $:
$$ \Delta_x = \begin{vmatrix} x' - 5 & -3 \\ y' + 2 & 4 \end{vmatrix} $$
$$ \Delta_x = 4(x' - 5) + 3(y' + 2) = 4x' - 20 + 3y' + 6 = 4x' + 3y' - 14 $$
So: $$ x = \frac{ \Delta_x }{ \Delta } = \frac{4x' + 3y' - 14}{11} $$
Now compute $ \Delta_y $ by replacing the second column:
$$ \Delta_y = \begin{vmatrix} 2 & x' - 5 \\ 1 & y' + 2 \end{vmatrix} $$
$$ \Delta_y = 2(y' + 2) - (x' - 5) = 2y' + 4 - x' + 5 = -x' + 2y' + 9 $$
So: $$ y = \frac{ \Delta_y }{ \Delta } = \frac{-x' + 2y' + 9}{11} $$
Therefore, the inverse transformation is:
$$ \begin{cases} x = \dfrac{4x' + 3y' - 14}{11} \\ y = \dfrac{-x' + 2y' + 9}{11} \end{cases} $$
This confirms that the mapping is reversible: bijectivity is ensured.
Geometrically, this means each point in the plane corresponds to one and only one image point, and vice versa.

Note. We can also derive the inverse equations using the inverse of the coefficient matrix. Starting again from: $$ \begin{cases} 2x - 3y = x' - 5 \\ x + 4y = y' + 2 \end{cases} $$
Let’s express the system in matrix form:
$$ A \cdot \vec{x} = \vec{b} $$
Where $A = \begin{pmatrix} 2 & -3 \\ 1 & 4 \end{pmatrix}$ is the coefficient matrix, $\vec{x} = \begin{pmatrix} x \\ y \end{pmatrix}$ is the variable vector, and $\vec{b} = \begin{pmatrix} x' - 5 \\ y' + 2 \end{pmatrix}$ is the constants vector.
$$ \begin{pmatrix} 2 & -3 \\ 1 & 4 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x' - 5 \\ y' + 2 \end{pmatrix} $$
We isolate $\vec{x}$ as follows:
$$ \vec{x} = A^{-1} \cdot \vec{b} $$
The inverse matrix $A^{-1}$ is computed by: $$ A^{-1} = \frac{1}{\det(A)} \begin{pmatrix} e & -b \\ -d & a \end{pmatrix} = \frac{1}{11} \begin{pmatrix} 4 & 3 \\ -1 & 2 \end{pmatrix} $$
Substitute into the matrix equation: $$ \vec{x} = \frac{1}{11} \begin{pmatrix} 4 & 3 \\ -1 & 2 \end{pmatrix} \begin{pmatrix} x' - 5 \\ y' + 2 \end{pmatrix} $$
Computing the individual components:
$$ x = \frac{1}{11} \left[ 4(x' - 5) + 3(y' + 2) \right] = \frac{4x' + 3y' - 14}{11} $$
$$ y = \frac{1}{11} \left[ -1(x' - 5) + 2(y' + 2) \right] = \frac{-x' + 2y' + 9}{11} $$
Therefore, the inverse transformation is: $$ \begin{cases} x = \dfrac{4x' + 3y' - 14}{11} \\ y = \dfrac{-x' + 2y' + 9}{11} \end{cases} $$
This matches the result obtained using Cramer’s Rule.
How to Apply a Geometric Transformation to a Function
When working with a function - say a parabola like \( y = x^2 \) - and you want to see how it changes under a geometric transformation, you need to shift its points according to specific rules.
- Find the inverse of the transformation \( t \), which means expressing \( x \) and \( y \) in terms of the new variables \( x' \) and \( y' \).
- Substitute these expressions into the original function.
- Rewrite the equation in terms of the new coordinates \( x' \) and \( y' \).
Example
Let’s start with the function:
$$ y = x^2 $$
Now consider the geometric transformation:
$$ t: \begin{cases} x' = x + 1 \\ y' = y - 2 \end{cases} $$
First, we find the inverse of the transformation - that is, we express \( x \) and \( y \) in terms of \( x' \) and \( y' \):
$$ \begin{cases} x' = x + 1 \Rightarrow x = x' - 1 \\ y' = y - 2 \Rightarrow y = y' + 2 \end{cases} $$
So, the inverse transformation \( t^{-1} \) is:
$$ t^{-1} : \begin{cases} x = x' - 1 \\ y = y' + 2 \end{cases} $$
We now substitute \( x = x' - 1 \) and \( y = y' + 2 \) into the original equation:
$$ y = x^2 $$
$$ y' + 2 = (x' - 1)^2 $$
$$ y' + 2 = x'^2 - 2x' + 1 $$
$$ y' = x'^2 - 2x' + 1 - 2 $$
$$ y' = x'^2 - 2x' - 1 $$
So, after applying the transformation, the function \( y = x^2 \) becomes \( y' = x'^2 - 2x' - 1 \).
This transformation shifts the graph 1 unit to the right (since \( x' = x + 1 \)) and 2 units down (since \( y' = y - 2 \)).
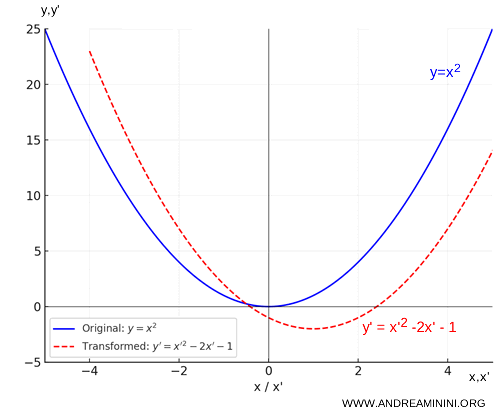
The parabola moves down and to the right, but its overall shape remains unchanged.
Observations
Some observations and side notes:
- Geometric transformations can be represented mathematically using equations, matrices, or functions. For example, a translation can be expressed by adding a constant vector to each point, while a rotation can be represented by a rotation matrix. And so on.
And so on.
