Homothety
Homothety is a geometric transformation that maps the points of a figure relative to a fixed point O, altering the distances between the points proportionally by a factor k, while keeping the shape of the figure unchanged.
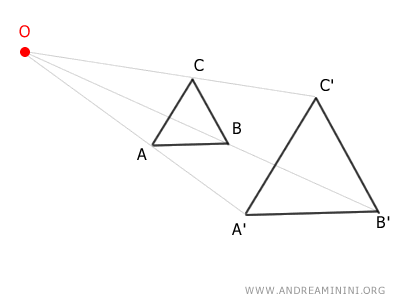
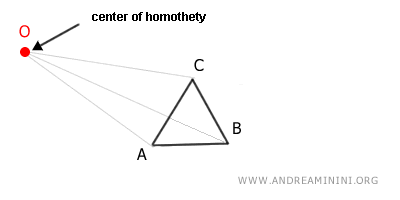
The point O is called the center of homothety, and the factor k is known as the homothety ratio.
Direct and inverse Homothety
In simpler terms, homothety can shrink or enlarge a figure while maintaining the alignment of the points (collinearity) and preserving the relative distances between them.
For instance, consider a figure ABC and select point O as the center of homothety, with a value of k as the homothety ratio.
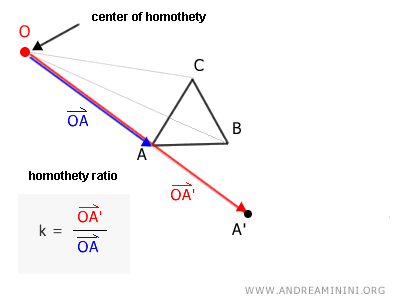
Now, take the vector $ \overrightarrow{OA} $ and multiply it by the homothety ratio k, resulting in another vector $ \overrightarrow{OA'} $ that shares the same origin and direction as the original (O) but with a different length.
$$ \overrightarrow{OA'} = k \times \overrightarrow{OA} $$
This helps us identify another point A' on the plane that lies along the same line as OA.
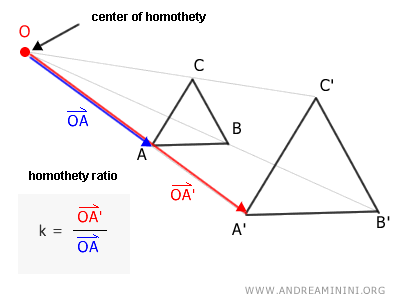
So, if A is a point on the original figure and A' is its corresponding point in the homothetic figure, then the points O, A, and A' are aligned, and the segment OA' is k times the length of the segment OA.
Note: I’m using vectors (e.g., $ \overrightarrow{OA} $) instead of segments (e.g., $ \overline{OA} $) because in homothety, it’s crucial to consider the direction of the geometric transformation. This is because the homothety ratio k can be negative (k<0), which would indicate an "inverse homothety."
If I repeat this process for the other points B and C of the original figure, I end up with another figure A'B'C' that is similar to the original one.
The figure A'B'C' retains the same shape as the figure ABC but differs in size.
In this case, the transformed figure is enlarged.
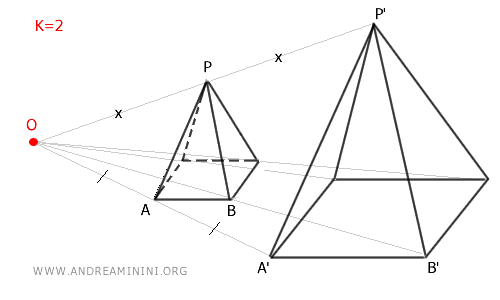
Depending on the homothety ratio (k), different effects can be observed:
- If |k| > 1, the homothety results in an enlargement.
- If |k| < 1, the homothety results in a reduction.
- If k = 1, the homothety is an identity transformation, meaning the figure remains unchanged.
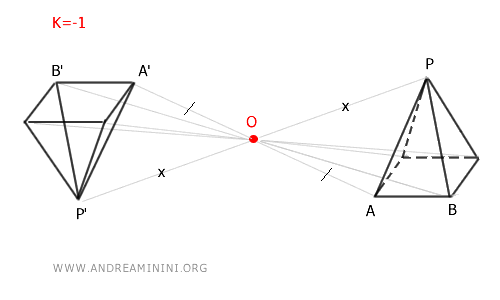
- If k = -1, the homothety is equivalent to central symmetry.
It's important to remember that the homothety ratio can also be negative (k<0).
The sign of the homothety ratio determines the type of homothety: direct or inverse.
- Direct Homothety
If k>0, the homothety is referred to as direct because the corresponding points remain in the same quadrant.
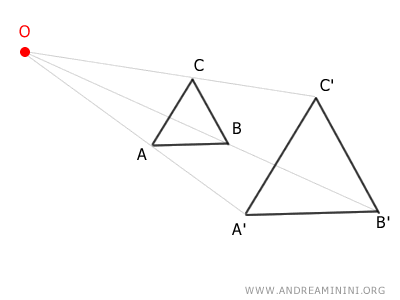
- Inverse Homothety
If k < 0, the homothety is referred to as inverse, as it not only causes a reduction or enlargement but also a reflection with respect to the homothety center O.
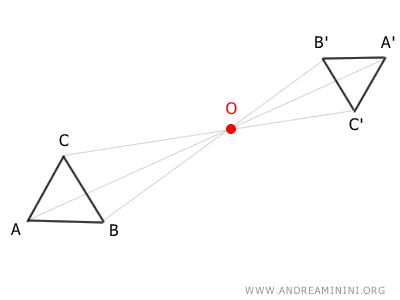
What’s the purpose? Homothety is used to enlarge or reduce geometric figures while maintaining their proportions and original shapes. It is especially useful for studying relationships between similar figures.
A Practical Example
Let's consider a square with a side length of a and a homothety center at its center O.
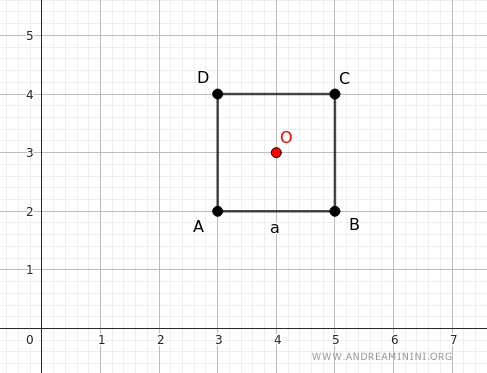
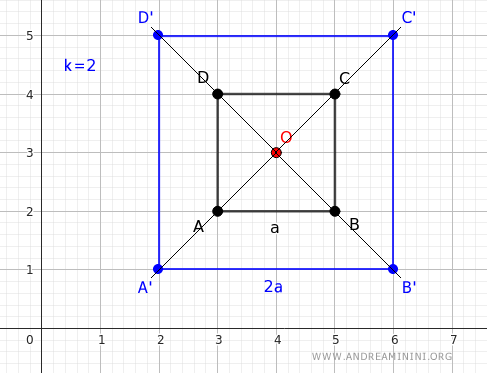
If I apply a homothety with a ratio of k=2, I get a square with a side length of 2a.
The result is an enlargement.
If I apply a homothety with a ratio of k = 0.5, I get a square with a side length of a/2.
In this case, the result is a reduction.
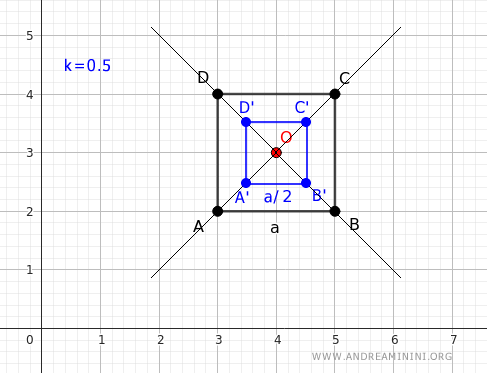
Obviously, with the same ratio k, the result changes depending on the chosen homothety center.
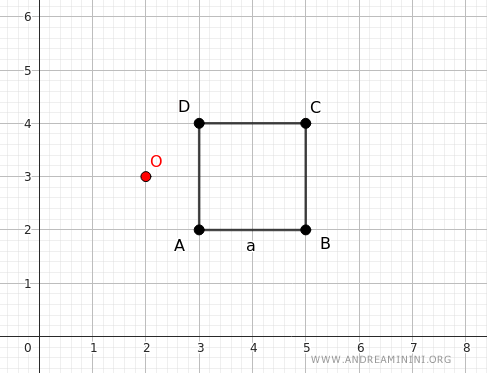
For example, consider the same square but with the homothety center at O(2,3).
If I apply a homothety with a ratio of k=2, I get a square with a side length of 2a.
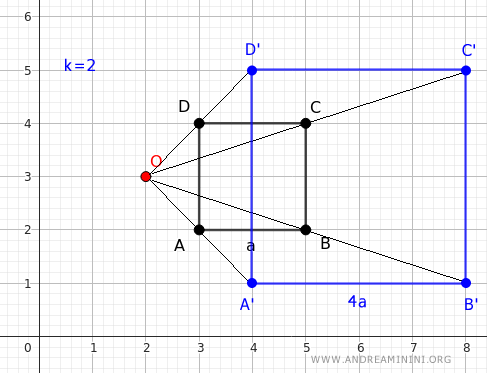
The result is completely different from the previous one.
Equations of Homothety
These equations provide a simplified representation of homothety in Cartesian coordinates when the homothety center is at the origin O(0,0) of the Cartesian plane.
$$ \begin{cases} x' = k \cdot x \\ \\ y' = k \cdot y \end{cases} $$
Where k is the homothety ratio, (x, y) are the coordinates of a point in the original figure, and (x', y') are the coordinates of the corresponding point in the homothetic figure.
Therefore, the equations of the inverse homothety are:
$$ \begin{cases} x = \dfrac{1}{k} \cdot x' \\ \\ y = \dfrac{1}{k} \cdot y' \end{cases} $$
If the homothety center O is not at the origin but at another point O(x0,y0), the equations become slightly more complex.
$$ \begin{cases} x' = x_0 + k \cdot (x - x_0) \\ \\ y' = y_0 + k \cdot (y - y_0) \end{cases} $$
These equations describe how each point of the original figure is mapped to the homothetic figure with respect to the center O(x0, y0).
Example: In this case, the homothety ratio is k=2, and the homothety center is at the coordinates O(2,3), so x0=2 and y0=3.
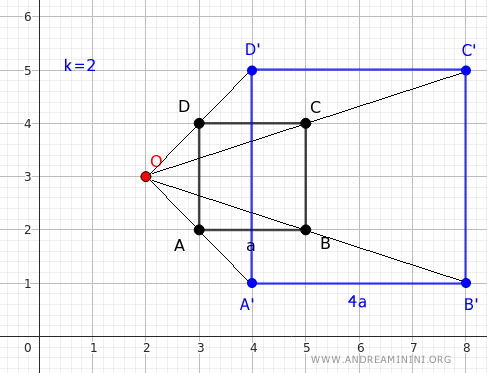
Point A is located at the coordinates (x, y) = (3, 2). I use the equations to calculate the coordinates (x', y') of the corresponding point A' after the geometric transformation: $$ \begin{cases} x' = x_0 + k \cdot (x - x_0) \\ \\ y' = y_0 + k \cdot (y - y_0) \end{cases} $$ Applying the homothety ratio k=2: $$ \begin{cases} x' = x_0 + 2 \cdot (x - 2) \\ \\ y' = y_0 + 2 \cdot (y - 3) \end{cases} $$ Substituting x0=2 and y0=3: $$ \begin{cases} x' = 2 + 2 \cdot (x - 2) \\ \\ y' = 3 + 2 \cdot (y - 3) \end{cases} $$ Now, using the coordinates of point A (x=3, y=2): $$ \begin{cases} x' = 2 + 2 \cdot (3 - 2) \\ \\ y' = 3 + 2 \cdot (-1) \end{cases} $$ $$ \begin{cases} x' = 4 \\ \\ y' = 1 \end{cases} $$ So, the coordinates of the corresponding point A' are x'=4 and y'=1. $$ \begin{cases} x' = 4 \\ \\ y' = 1 \end{cases} $$ Using the same method, you can calculate the corresponding points B', C', and D'.
Homothety in Three-Dimensional Space
Homothety in three-dimensional space is a geometric transformation that scales figures while preserving their proportions, relative to a fixed point called the center of homothety. It maintains the ratio of distances, ensuring that the transformed shape remains similar to the original.
This transformation extends the concept of homothety from the plane to three-dimensional space, affecting all points within it.
Let \( O \) be a fixed point in space, and let \( k \neq 0 \) be a real number known as the homothety ratio.
A homothety centered at \( O \) with ratio \( k \) transforms each point \( P(x, y, z) \) into \( P'(x', y', z') \) according to the equation:
\[ P' = O + k (P - O) \]
In coordinate form, if \( O(x_0, y_0, z_0) \) and \( P(x, y, z) \), then the transformed point \( P'(x', y', z') \) is given by:
\[ x' = x_0 + k (x - x_0) \]
\[ y' = y_0 + k (y - y_0) \]
\[ z' = z_0 + k (z - z_0) \]
In simpler terms, each point \( P \) moves along the line passing through \( O \) and \( P \), with its distance from \( O \) scaled by the factor \( k \).
Direct and Inverse Homothety
Homothety in three-dimensional space can be classified as either direct or inverse, depending on the value of \( k \).
- Direct homothety
When \( k > 0 \), the transformation is direct: points move radially outward or inward from \( O \) while maintaining the same orientation. If \( k > 1 \), the figure enlarges; if \( 0 < k < 1 \), it shrinks. For example, with \( k = 2 \), the solid doubles in size. If \( k = 1 \), the transformation has no effect, leaving the figure unchanged.

- Inverse homothety
When \( k < 0 \), the transformation is inverse: points are reflected across \( O \) and appear on the opposite side of the line \( OP \), effectively flipping the object. If \( k = -1 \), the figure is reflected symmetrically across \( O \), maintaining congruence with the original but reversing its orientation.
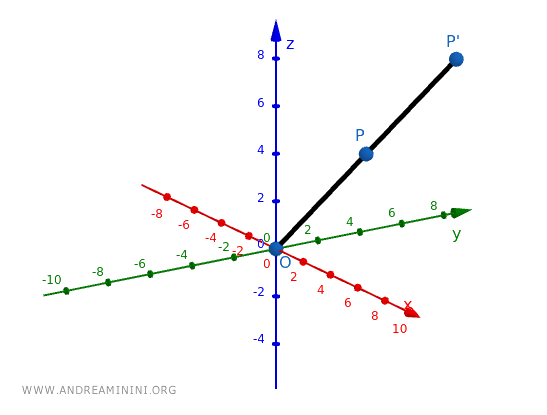
Example 1
Applying a direct homothety with \( k = 2 \) to a cube centered at \( O \) doubles its dimensions while preserving its shape and orientation.
Consider a point \( P(2, 3, 4) \) and apply a homothety centered at \( O(0,0,0) \) with \( k = 2 \):
\[ x' = 0 + 2(2 - 0) = 4 \]
\[ y' = 0 + 2(3 - 0) = 6 \]
\[ z' = 0 + 2(4 - 0) = 8 \]
The new point is \( P'(4, 6, 8) \), which lies along the same line as \( P \) relative to \( O \), but twice as far away.
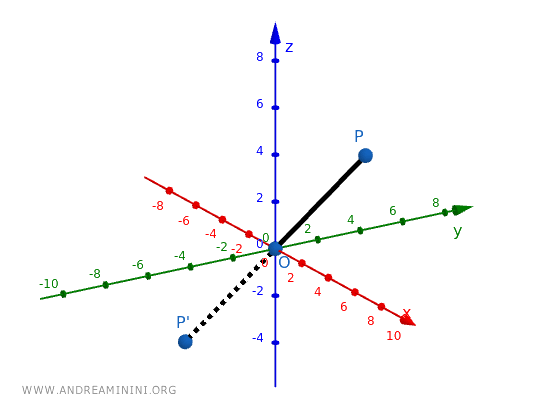
Example 2
In an inverse homothety, the transformed object is reflected across \( O \), reversing its orientation. If a homothety with \( k = -1 \) is applied to a cube, the cube is flipped relative to \( O \).
Using the same point \( P(2, 3, 4) \) and applying a homothety with \( k = -1 \):
\[ x' = 0 + (-1)(2 - 0) = -2 \]
\[ y' = 0 + (-1)(3 - 0) = -3 \]
\[ z' = 0 + (-1)(4 - 0) = -4 \]
The new point is \( P'(-2, -3, -4) \), which is the reflection of \( P \) across \( O \).
In summary, direct homothety preserves orientation, while inverse homothety flips the object in space.
Key Properties of Homothety in Space
Homothety in three-dimensional space exhibits the following properties:
- Similarity: Homothetic figures are similar to the original, preserving proportional distances.
- Collinearity: If three points were collinear before the transformation, they remain collinear afterward.
- Parallelism: Parallel planes remain parallel after the transformation.
- Area and Volume Scaling:
- If an object has an area \( A \), applying a homothety with ratio \( k \) results in a new area \( A' = k^2 A \).
- If an object has a volume \( V \), after homothety, the volume becomes \( V' = k^3 V \).
Key Observations
Here are some key observations and properties of homothety:
- Homothety is not an isometric transformation
Since the absolute distances between points change, it’s clear that, except when k=1, homothety is not an isometric transformation. However, like isometries, homothety preserves certain invariant properties of figures, such as angle magnitudes, collinearity (alignment of points), and proportions between distances of points.
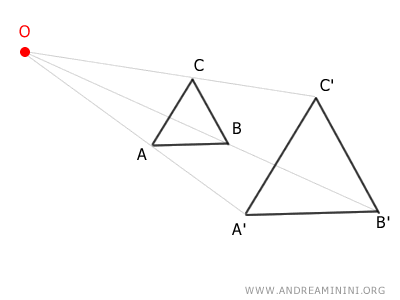
Some key properties of a homothety:- A homothety always maps a line segment to another segment proportional to it.
- It preserves the measures of all angles.
- The center of the homothety is the only fixed point under the transformation.
- Every line passing through the center remains invariant as a whole.
- Proportionality of distances
The distances between points in the homothetic figure are proportional to the corresponding distances in the original figure. Thus, the relative distances between points remain unchanged in homothety (even though absolute distances do not).
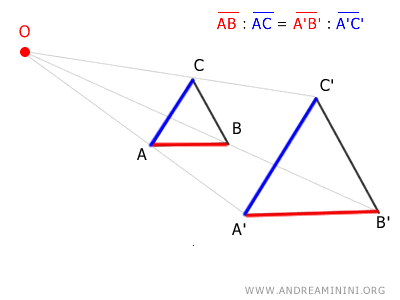
For example, the segment AB is to segment AC as segment A'B' is to segment A'C'. This proportion holds: $$ \overline{AB}:\overline{AC} = \overline{A'B'}: \overline{A'C'} $$
- Conservation of angles
The angles in the original figure and in the homothetic figure (the transformed figure) are congruent, meaning they have the same measure.
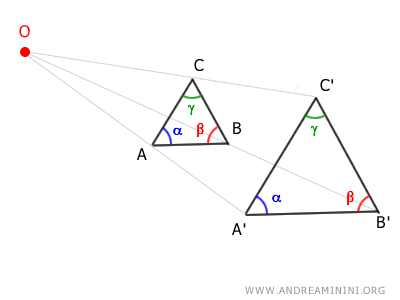
- Invariance of the center
The center of homothety (O) remains unchanged by the transformation and is the only fixed point in the homothety.

- When the homothety ratio is k=-1, homothety equals central symmetry
When the homothety ratio is k=-1, the transformation vectors have the same origin and direction but opposite orientation. In this specific case, the final result is identical to that of a central symmetry with the same center O.
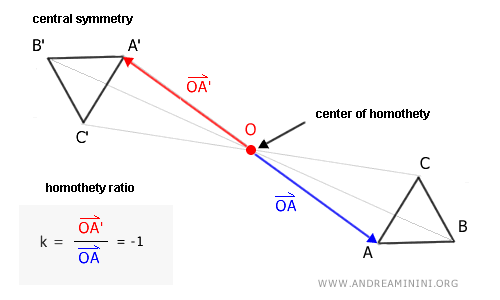
Note: In this particular case, the sides of the original figure and those of the transformed figure are congruent. $$ \overline{AB} \cong \overline{A'B'} \\ \overline{AC} \cong \overline{A'C'} \\ \overline{BC} \cong \overline{B'C'} $$
- The composition of two homotheties sharing the same center is itself a homothety with that center
When two homotheties $ T_1 $ and $ T_2 $ share the same center $ O $, their composition is again a homothety centered at $ O $, whose scale factor is the product of the two ratios: $ k = k_1 \cdot k_2 $.Indeed, if $$ T_1 : \begin{cases} x' = k_1 x \\ \\
y' = k_1 y \end{cases} \quad\text{and}\quad T_2 : \begin{cases} x' = k_2 x \\ \\ y' = k_2 y \end{cases} $$ then their composition $ T_1 \circ T_2 $ becomes: $$ T_1 \circ T_2 : \begin{cases} x' = k_1 (k_2 x) = (k_1 k_2)x \\ \\ y' = k_1 (k_2 y) = (k_1 k_2)y \end{cases} $$ Hence, $$ T_1 \circ T_2 = H(O, k_1 k_2) $$ meaning that the result is a homothety with center $ O $ and scale factor $ k = k_1 k_2 $.Note. All homotheties with the same center form a group under composition, since they satisfy the defining properties:
- Closure: the composition of two homotheties is still a homothety with the same center;
- Associativity: composition of transformations is associative by definition;
- Existence of an identity element ($ k = 1 $), corresponding to the identity homothety;
- Existence of inverses: every homothety with ratio $ k $ has an inverse homothety with ratio $ k^{-1} = \frac{1}{k} $.
And so forth.
