Fixed Point in geometry

A point is called a fixed point (or invariant point) of a geometric transformation if its position remains unchanged after the transformation is applied.

In other words, if a point keeps the same coordinates before and after the transformation, it is considered a fixed point of that transformation.

Formally, given a function \( T: \mathbb{R}^2 \to \mathbb{R}^2 \), a point \( P \) is a fixed point if \( T(P) = P \).

For example, in a rotation on a plane, the center \( P \) of the rotation is a fixed point because it stays in the same position.

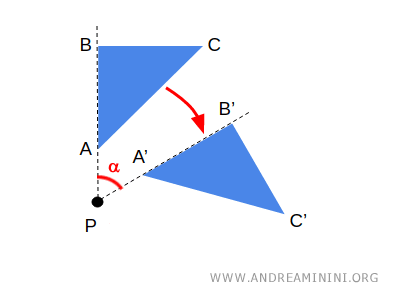
There can be multiple fixed points.

For instance, in an axial symmetry with respect to a line \( r \), every point on the symmetry axis \( r \) remains unchanged.

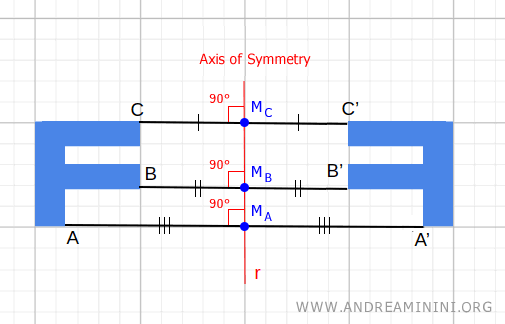
In some cases, every point in a transformation is fixed.

For example, a full 360° rotation of a plane figure around a central point \( P \) leaves all points exactly where they started.

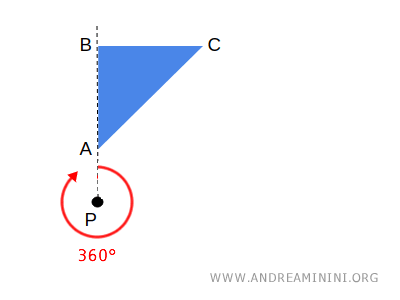
In this scenario, all points are fixed, and the entire figure is known as a invariant figure under the transformation.

On the other hand, some transformations have no fixed points at all.

For instance, in a translation, no point remains fixed unless the translation is trivial (i.e., zero displacement).

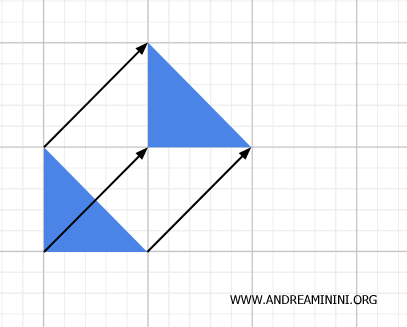
These are just a few examples of fixed points in geometric transformations.

Note. The concept of a fixed point extends seamlessly from two-dimensional to three-dimensional space. A point is considered fixed if its coordinates remain unchanged after the transformation. The only difference in three-dimensional space is that a point is described by three coordinates, \((x, y, z)\), instead of two, \((x, y)\).

And so on.