Similarity

Similarity is a geometric transformation that preserves the shape of a figure. It keeps all corresponding angles congruent and maintains a constant ratio $ k $ between corresponding sides. Any similarity can be obtained by combining a homothety with an isometry.

A similarity is commonly denoted by the lowercase Greek letter sigma, $ \sigma $.

It is a geometric transformation that preserves the shape of a figure while altering its size.

In other words, two figures are called similar if one can be obtained from the other through a similarity. This occurs if they satisfy both of the following conditions:

1. Their corresponding angles are congruent
2. Their corresponding sides are proportional, with the same similarity ratio $ k $ for every pair of corresponding sides

Hence, a figure similar to another keeps the same shape but changes its dimensions.

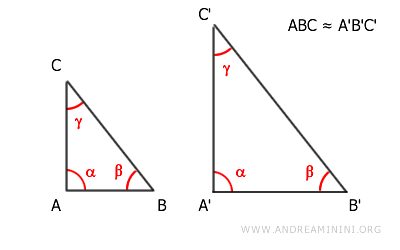
The symbol used to express similarity is "≈".

For example, to state that triangles ABC and A'B'C' are similar, we write:

$$ ABC ≈ A'B'C' $$

The corresponding sides and angles in a similarity are known as corresponding sides and corresponding angles.

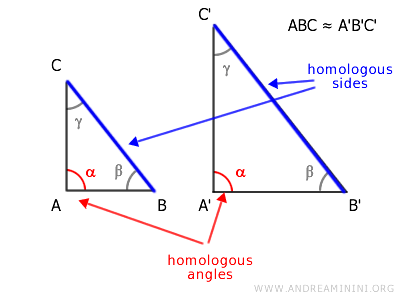
Note. In similar triangles, corresponding sides are those opposite congruent angles. In other words, corresponding sides are the sides opposite matching angles.

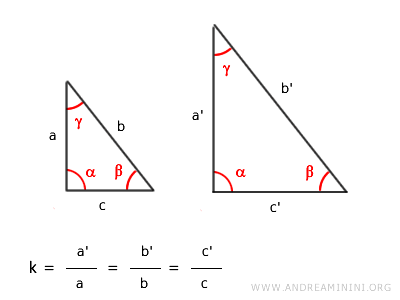
The proportionality ratio $ k $ is the same for all corresponding sides and is also called the similarity ratio or scale factor.

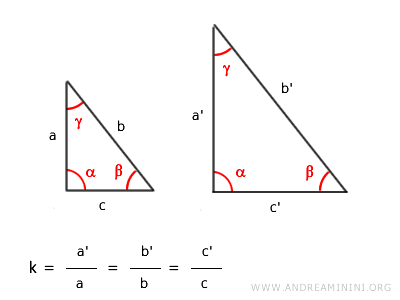
Therefore, the invariants of a similarity are the angle measures and the ratios between corresponding segments.

• It preserves length ratios.
• It preserves angle measures, since every angle is mapped to a congruent one.
• If two lines are perpendicular in the original figure, they remain perpendicular in the similar one. Likewise, parallel lines remain parallel.

As a result, similarity preserves parallelism: if two sides of a figure are parallel, their corresponding sides in the similar figure are also parallel (affinity).

A common real-world example of similarity is enlarging a photograph. The enlarged photo and the original have the same shape, although their sizes differ.

Similarity also extends to three-dimensional geometry. Two solids are similar if their corresponding angles are congruent and their corresponding edges are parallel, with the same proportionality ratio |k|.

The similarity ratio

When two figures are similar, the lengths of their corresponding sides are proportional. This constant ratio is called the similarity ratio or scale factor. The similarity ratio is always positive ( $ k > 0 $ ).

• Enlargement (k>1)
  If the similarity ratio is greater than 1, the image is an enlargement with scale 1:k.

  
  For example, if k=2, the figure is enlarged by a factor of 2. Each length in the similar figure is twice the corresponding length in the original.

• Isometry (k=1)
  If the similarity ratio is equal to 1, the transformation is an isometry such as a rotation, translation or reflection.
  
• Reduction (0<k<1)
  If the similarity ratio lies between 0 and 1, the figure is reduced with scale 1:k.
  

  For example, if k=0.5, the figure is reduced at a scale of 1:0.5, which is equivalent to a scale of 2:1.

In every case, similar figures always preserve the same shape.

Similar Polygons

Polygons are considered similar if their corresponding sides are in constant proportion and their angles match in measure, ensuring their shapes are congruent.

By extension, all regular polygons and circles are inherently similar to one another.

Criteria for Triangle Similarity

Specific criteria define similarity between geometric figures, particularly triangles, such as:

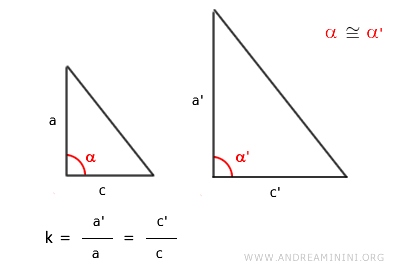
• AAA Criterion (Angle-Angle-Angle)
  Triangles with congruent corresponding angles are similar, confirming similarity through angular congruence alone.
  

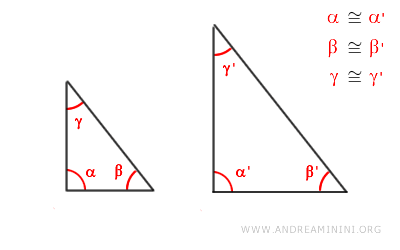
  Note: In practice, verifying two congruent angles is sufficient to establish similarity between triangles, as the third angle will inherently be congruent due to the constant sum of angles in a triangle equating to 180 degrees.

• SAS Criterion (Side-Angle-Side)
  Similarity is also established when two sides of a triangle are proportional to those of another, with the included angles being equal.
  
• SSS Criterion (Side-Side-Side)
  Triangles with proportional sides are deemed similar, indicating a uniform scale factor across all corresponding sides.
  

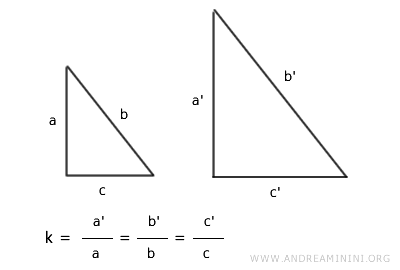
Equations of Similarity

The mathematical representation of similarity in the Cartesian plane involves a system of matrix equations, illustrating the transformation's effect on coordinates.

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = M \cdot \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} c \\ d \end{pmatrix} $$

Where M varies, depending on the nature of similarity, whether direct or inverse.

• Direct Similarity $$ M = \begin{pmatrix} a & -b \\ b &a \end{pmatrix} $$
• Inverse Similarity $$ M = \begin{pmatrix} a & b \\ b & -a \end{pmatrix} $$

Direct and inverse similarities thus follow distinct Cartesian systems, with the similarity ratio k calculated as:

$$ k = \sqrt{a^2+b^2} $$

Alternatively, similarity can be expressed through trigonometric forms, further demonstrating its flexibility in geometric transformations.

Example

Consider the following geometric transformation.

\[ \tau:\; \begin{cases} x' = 2x + y + 1 \\ \\ y' = x - 2y - 1 \end{cases} \]

The matrix of its linear part is

\[ A= \begin{pmatrix} 2 & 1\\ 1 & -2 \end{pmatrix} \]

This defines an opposite similarity, since the matrix has the form \(\begin{pmatrix} a & b \\ b & -a \end{pmatrix}\) with \(a=2\) and \(b=1\).

Compute the determinant of \(A\)

\[ \det A= \det \begin{pmatrix} 2 & 1\\ 1 & -2 \end{pmatrix} = (2)(-2) - (1)(1) = -4 - 1 = -5 \]

The determinant is negative, so the orientation of the figure is reversed.

Now compute the scale factor of the similarity:

\[ k=\sqrt{a^2+b^2}=\sqrt{2^2+1^2}=\sqrt{5} \]

The transformation \(\tau\) is therefore an opposite similarity with scale factor \(k=\sqrt{5}\), which multiplies all lengths by \(k\).

Apply \(\tau\) to the isosceles right triangle \(OAB\) with vertices \(\,O(0,0),\;A(1,0),\;B(0,1)\).

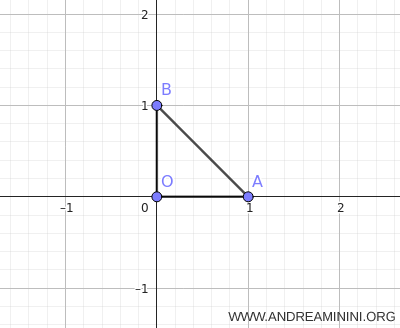
Compute the images of the three vertices.

• Point \(O\):
  \[ x'_O = 2\cdot 0 + 0 + 1 = 1,\qquad y'_O = 0 - 2\cdot 0 - 1 = -1 \] The image is \(O'(1,-1)\).
• Point \(A\):
  \[ x'_A = 2\cdot 1 + 0 + 1 = 3,\qquad y'_A = 1 - 2\cdot 0 - 1 = 0 \] The image is \(A'(3,0)\).
• Point \(B\):
  \[ x'_B = 2\cdot 0 + 1 + 1 = 2,\qquad y'_B = 0 - 2\cdot 1 - 1 = -3 \] The image is \(B'(2,-3)\).

Explanation. To find the transformed coordinates \((x',y')\), substitute each original point \((x,y)\) into the system. For instance, if \(O=(0,0)\): \[ \tau:\; \begin{cases} x' = 2x + y + 1 \\ \\ y' = x - 2y - 1 \end{cases} \] Substitute \(x=0\) and \(y=0\): \[ \tau:\; \begin{cases} x' = 2 \cdot 0 + 0 + 1 \\ \\ y' = 0 - 2 \cdot 0 - 1 \end{cases} \] \[ \tau:\; \begin{cases} x' = 1 \\ \\ y' = -1 \end{cases} \] So the image is \(O'(1,-1)\).

After the transformation, the triangle \(O'A'B'\) has vertices \(O'(1,-1)\), \(A'(3,0)\), and \(B'(2,-3)\).

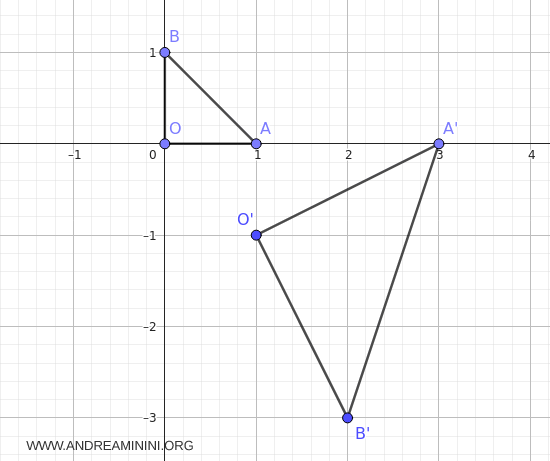
In the original triangle \(OAB\), the side lengths were \(\overline{OA}=1\), \(\overline{OB}=1\), and \(\overline{AB}=\sqrt{2}\).

In the transformed triangle \(O'A'B'\), obtained through a similarity with scale factor \(k=\sqrt{5}\), the corresponding side lengths are:

• \( O'A' = k \cdot OA = \sqrt{5} \cdot 1 = \sqrt{5}\)
• \( O'B' = k \cdot OB = \sqrt{5} \cdot 1 = \sqrt{5}\)
• \( A'B' = k \cdot AB = \sqrt{5} \cdot 2 = \sqrt{10}\)

All lengths are multiplied by \(\sqrt{5}\). The orientation is reversed, while angles and proportions are preserved. The resulting figure is still an isosceles right triangle.

Spatial Similarity

Spatial similarity is defined in much the same way as similarity in a plane.

It is a geometric transformation that results from combining an isometry (a transformation that preserves distances, such as translations, rotations, and reflections) with a dilation (a transformation that enlarges or shrinks an object while maintaining its proportions).

Key Properties of Spatial Similarity

Spatial similarity has the following properties:

• It preserves angles between geometric elements.
• It transforms line segments into proportional segments, maintaining a constant similarity ratio.
• The similarity ratio is the same as the dilation factor and determines the scale of the transformation.

Real-World Examples of Spatial Similarity

If a structure is scaled with a similarity ratio of \( k = 2 \), all its dimensions - length, height, and depth - will double in size compared to the original.

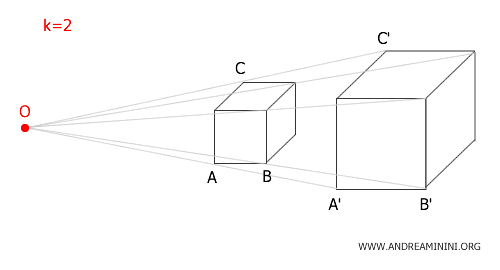
On the other hand, if a solid undergoes a transformation with a similarity ratio of \( k = \frac{1}{2} \), its edges will be half as long as those of the original, but its overall shape will remain unchanged.

Observations

Exploring the nuances of similarity, we encounter several key insights:

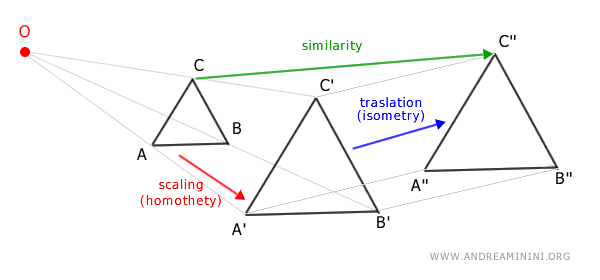
• A similarity is equivalent to the composition of a homothety and an isometry
  In the plane, a similarity can be expressed as the composition of a homothety and an isometry (such as a translation, rotation, axial or central reflection, or the identity), in either order. Below is a practical example illustrating how a homothety and an isometry combine to produce a similarity.
  
• The composition of two similarities is itself a similarity
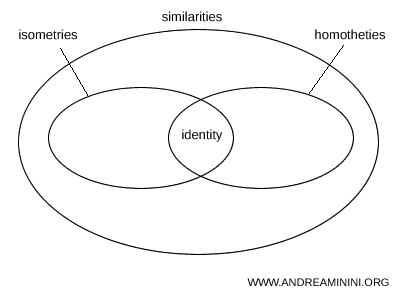
  When two similarities with scale factors k₁ and k₂ are combined, the result is another similarity whose scale factor is the product k₁·k₂.
• Isometries and homotheties as specific types of similarities
  Isometries and homotheties belong to the broader class of similarities, which includes all plane transformations that preserve angles and proportional relationships between lengths.
  • An isometry is a similarity with a unit scale factor $ k = 1 $, meaning all distances remain unchanged.
  • A homothety is a similarity with a fixed center and no rotation or translation. It multiplies every distance from that center by a constant factor $ k $.
  Thus, every isometry and homothety is a similarity. However, not all similarities fall into these two categories:
  • Not every similarity is an isometry, because the scale factor can differ from one ( $ k \ne 1 $ ), whereas in isometries it must be $ k = 1 $.
  • Not every similarity is a homothety, since a similarity may also include rotations, translations, or reflections in addition to dilation.
  Therefore, isometries and homotheties are subsets of the broader set of similarities. The set of all similarities is more general, including isometries when $ k = 1 $ and homotheties when there is no rotation or translation.
  
• Congruent figures are also similar
  Any pair of congruent geometric figures are necessarily similar. Indeed, a congruence can be interpreted as the composition of a homothety with any chosen center and scale factor 1, together with an isometry such as the identity, a translation, a rotation, or a reflection (axial or central).
• Center of a similarity
  In the plane, any similarity that is not a translation has a fixed point, meaning a point that maps to itself under the transformation. This invariant point is called the center of the similarity.
• Direct and indirect similarities
  In the plane, a similarity is called direct if it preserves orientation. If it reverses orientation, it is called an indirect similarity.
• The ratio of the perimeters of two similar figures
  In the plane, if two figures are similar with similarity ratio $ k $, then the ratio of their perimeters is also $ k $. In particular, if $ F' $ is the image of figure $ F $ under a similarity with ratio $ k $, then: $$ \text{Perimeter}(F') = k \cdot \text{Perimeter}(F) $$

  Note. A similarity multiplies every linear dimension by $ k $. Since the perimeter is a linear quantity, it is scaled by the same factor. For example, if the perimeter of a square is $ P = 4L $, then a similar square with side $ kL $ has $$ P' = 4(kL) = k \cdot (4L) = k \cdot P $$

• The ratio of the areas of two similar figures
  In the plane, if two figures are similar with similarity ratio $ k $, then the ratio of their areas is $ k^2 $. In particular, if $ F' $ is the image of figure $ F $ under a similarity with ratio $ k $, then: $$ \text{Area}(F') = k^2 \cdot \text{Area}(F) $$

  Note. A similarity multiplies every length by $ k $. Since area depends on two linear dimensions, the scale factor becomes $ k \cdot k = k^2 $. For example, if the area of a square is $ A = L \cdot L $, then a similar square with side $ kL $ has $$ A' = (kL) \cdot (kL) = k^2 \cdot (L \cdot L) $$

• The ratio of the volumes of two similar solids
  In three-dimensional space, if two solids are similar with similarity ratio \(k\), then the ratio of their volumes is \(k^3\). In particular, if \(F'\) is the image of solid \(F\) under a similarity with ratio \(k\), then: \[ \text{Volume}(F') = k^3 \cdot \text{Volume}(F) \]

  Note. A similarity scales every length by \(k\). Since volume depends on three linear dimensions, the scale factor becomes \(k^3\). For example, if a cube has side \(L\), its volume is \(V = L \cdot L \cdot L\). A similar cube with side \(kL\) has \[ V' = (kL)\cdot(kL)\cdot(kL) = k^3 \cdot (L \cdot L \cdot L) = k^3 \cdot V \]

Through this deeper dive into similarity, we uncover the intricate layers and principles that define geometric transformations, providing a comprehensive view of spatial relationships.