Perimeter Ratios in Similar Polygons

When it comes to similar polygons, the perimeter ratio matches the ratio of any pair of corresponding sides. $$ P : P' = l : l' $$ 

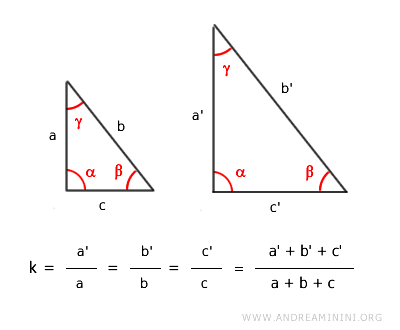
In layman's terms, if two polygons are similar, their perimeters reflect their scale factor, k.

This rule highlights that the similarity in shape carries over to the perimeters as well.

This theorem, however, applies strictly to similar polygons.

A Concrete Example

Consider two similar triangles, though the concept is applicable across all sorts of polygons, whether they’re regular or not.

 

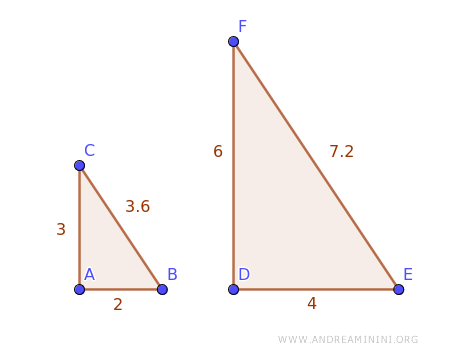
Here, the scale factor is simply k=2.

$$ \frac{6}{3} = \frac{4}{2} = \frac{7.2}{3.6} = 2 $$

The same goes for the perimeter ratio of these polygons, which is also 2.

$$ \frac{6+4+7.2}{3+2+3.6} = \frac{17.2}{8.6} = 2 $$

Thus, the perimeter ratio in similar polygons matches the scale factor of their corresponding sides.

The Proof

Take two similar polygons for example.

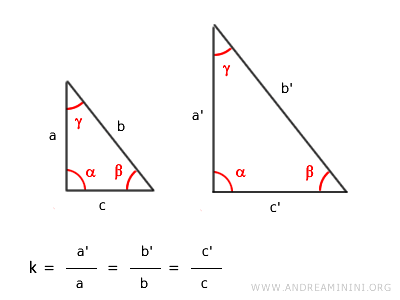
Similarity by definition means the sides correspond and are proportional.

$$ a : a' = b : b' = c : c' $$

This indicates a constant ratio across corresponding sides, equal to k:

$$ \frac{ a }{ a' } = \frac{ b }{ b' } = \frac{ c }{ c' } = k $$

With this consistency, it can also be expressed as:

$$ \frac{ a+b+c }{ a'+b'+c' } = k $$

Where the sum a+b+c=P is the first polygon's perimeter, and a'+b'+c'=P' represents the second's.

$$ \frac{ P }{ P' } = k $$

Knowing that the ratio between any two corresponding sides equals k

$$ \frac{ a }{ a' } = k $$

it follows their perimeters show the same scale factor.

$$ \frac{ P }{ P' } = \frac{ a }{ a' } = k $$

This confirms the perimeter ratio is directly tied to the ratio between corresponding sides of similar polygons.

$$ P : P' = a : a' $$

And there you have it.