Similarity Criteria for Polygons with the Same Number of Sides

This theorem, known as the Polygon Similarity Theorem, simplifies the process of establishing similarity between two polygons sharing the same number n of angles and sides.

In other words

1. The first criterion involves ignoring 3 consecutive angles
2. The second criterion skips over 2 consecutive angles and the sides between them
3. The third approach excludes 1 angle and the two sides adjacent to it

Note. Generally, to determine the similarity between two polygons, one should verify the congruence of all corresponding angles and the proportional similarity across all corresponding sides, requiring a more extensive set of checks.

Explanation

Similarity between polygons means they share the same shape but not necessarily the same size.

Therefore, to assess whether two polygons with n angles and sides are similar, one should check if both similarity conditions are met:

• all corresponding angles are congruent (meaning they have the same measure)
• all corresponding sides are proportional (i.e., the ratio between corresponding sides in the two polygons is constant).

Note. The mere presence of congruent corresponding angles is not sufficient to establish similarity in polygons with more than 3 sides. For example, a square and a rectangle have congruent corresponding angles (90°) but are not similar figures because their sides are not proportional, meaning the ratio between corresponding sides is not constant.

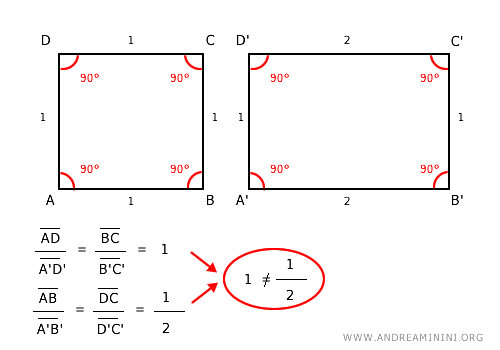
However, certain similarity criteria allow for the verification of similarity with fewer pieces of information.

Specifically, according to the Polygon Similarity Theorem, each of these scenarios suffices for establishing similarity:

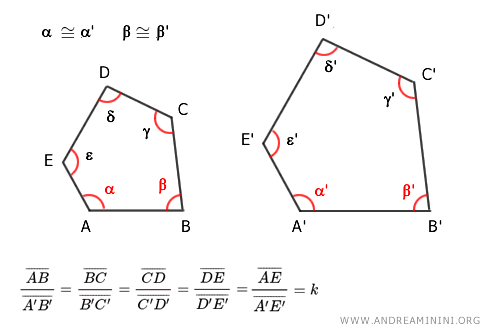
• Two polygons with n sides are similar if they have n-3 consecutive congruent angles and all corresponding sides are proportional. 

  Note. This criterion omits three consecutive angles from the check. For instance, these two pentagons have n=5 angles. Thus, I only need to check for congruence in n-3 consecutive angles, which means on 2 consecutive angles. In this example, I've chosen to verify the angles α= α' and β=β'. In addition, I must ensure that all corresponding sides share the same ratio of proportionality.
  

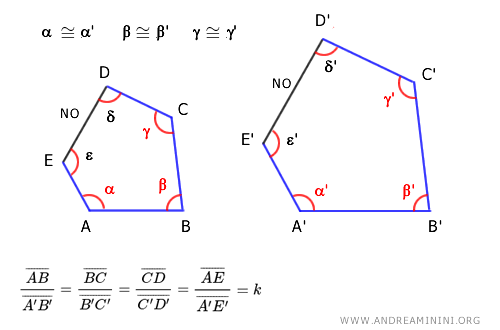
• Two polygons with n sides are similar if they have n-2 consecutive congruent angles and the respective adjacent sides are proportional.

  Note. This criterion excludes two consecutive angles and omits the side between them. For example, two pentagons have n=5 angles. Thus, congruence can only be verified on n-2 consecutive angles, which means on 3 consecutive angles. In this example, I opt to check congruence on angles α= α' , β=β' , and γ=γ' and the proportionality on the sides adjacent to them. I've excluded the remaining two angles δ and ε and the side DE between them.
  

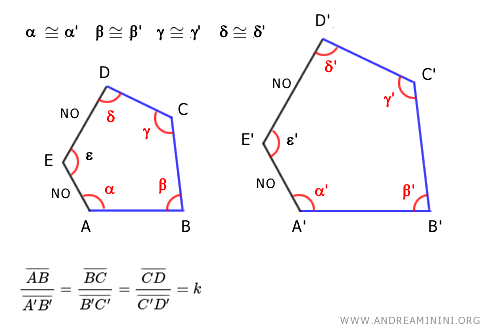
• Two polygons with n sides are similar if they have n-1 corresponding congruent angles and all sides not adjacent to the excluded angle are proportional

  Note. This criterion skips one angle and the two sides adjacent to the excluded angle. For example, in a pentagon with n=5 sides, congruence can be verified on n-1 angles, or on 4 angles, and the proportionality ratio only on the sides between them. If I exclude angle ε, it's sufficient to verify congruence on the remaining corresponding angles α≅α' , β≅β' , γ≅γ' , and δ≅δ' and the proportionality on all sides, except for the sides AE and DE adjacent to the excluded angle ε.
  

Similarity in Regular Polygons

An additional similarity criterion applies in the case of regular polygons.

Two regular polygons are similar if they have the same number n of sides.

This is a corollary of the Polygon Similarity Theorem.

Proof

Starting with the assumption of two regular polygons with n sides.

For instance, two regular pentagons with n=5 sides, but the principle applies regardless of the number of sides.

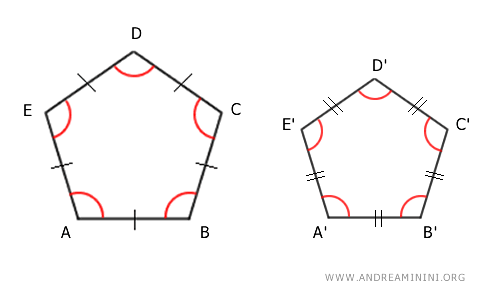
A polygon is considered "regular" if all its angles and sides are congruent, meaning they are of the same length.

1] All angles congruent

In a regular polygon, the angles are by definition all congruent, and the magnitude of each angle is determined by the number n of sides of the regular polygon:

$$ \frac{n-2}{n} \cdot 180° $$

This implies that all angles in a regular polygon are congruent to each other.

For example, in the case of a regular pentagon with n=5 sides, all have a magnitude of 108°.

$$ \frac{n-2}{n} \cdot 180° = \frac{5-2}{5} \cdot 180° = \frac{3}{5} \cdot 180° = 108° $$

Thus, if two regular polygons ABCDE and A'B'C'D'E' have the same number of sides, for example, n=5, I deduce that they also have congruent pairs of corresponding angles with the same magnitude.

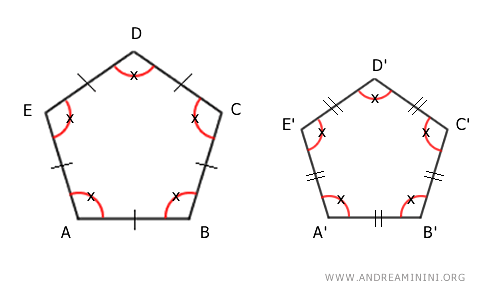
2 All sides congruent

In a regular polygon, all sides are congruent, meaning they are of the same length.

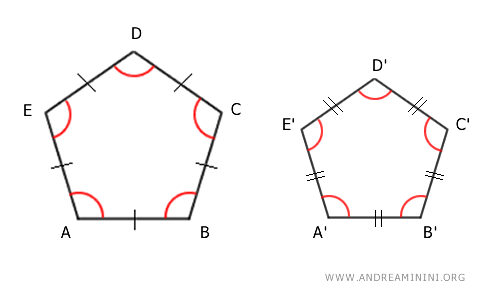
Therefore, all sides of the first polygon ABCDE are congruent to each other:

$$ \overline{AB} \cong \overline{BC} \cong \overline{CD} \cong \overline{DE} \cong \overline{AD} $$

For the same reason, all sides of the second polygon A'B'C'D'E' are congruent:

$$ \overline{A'B'} \cong \overline{B'C'} \ cong \overline{C'D'} \cong \overline{D'E'} \cong \overline{A'D'} $$

Taking a pair of corresponding sides from the two polygons, for example, AB and A'B', and calculating their ratio of proportionality.

$$ \frac{ \overline{AB}}{ \overline{A'B'} } = k $$

Knowing that all sides within the first polygon are congruent to each other, and the same holds true for the second polygon, I deduce that the other corresponding sides also share the same ratio of proportionality, k.

For instance, knowing AB≅BC and A'B'≅B'C' are congruent, then the ratio between sides BC and B'C' is equal to k.

$$  \frac{ \overline{AB}}{ \overline{A'B'} } = \frac{ \overline{BC}}{ \overline{B'C'} } = k $$

The same logic can be applied to all the other remaining sides.

$$ \frac{ \overline{CD}}{ \overline{C'D'} } = k $$

$$ \frac{ \overline{DE}}{ \overline{D'E'} } = k $$

$$ \frac{ \overline{AE}}{ \overline{A'E'} } = k $$

Hence, if two regular polygons have two corresponding sides that are proportional, it can be deduced that the other corresponding sides of the two polygons are proportionally the same.

Conclusion

In conclusion, in two regular polygons with the same number of sides, both similarity conditions are met:

1. all corresponding angles are congruent
2. all sides are proportional in the same manner

Therefore, the two polygons are similar.

Note. In other words, when dealing with two regular polygons with the same number of sides, there's no need to individually verify angle congruence or side proportionality. By definition, in regular polygons, all angles are equal to each other and all sides are of the same length, meaning that if two such polygons share the same number of sides, angle congruence and side proportionality are automatically assured, confirming their similarity.

And so on.

 

``