Similar Polygons Area Theorem
For two similar polygons, the ratio of their areas is equal to the square of their scale factor: $ \frac{A}{A'} = k^2 $.
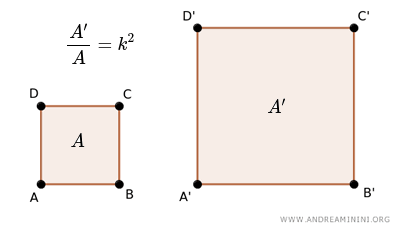
In simpler terms, the area ratio between two similar polygons is the square of the ratio of their corresponding side lengths.
$$ \frac{A'}{A} = k^2 = \left( \frac{l}{l'} \right)^2 $$
Where k represents the scale factor, and l, l’ are the lengths of corresponding sides in both polygons.
This means that if one polygon is k times as large as a similar counterpart, its area is k2 times that of the smaller polygon.
$$ A' = A \cdot k^2 $$
Thus, areas - being two-dimensional measures - scale by the square of the scaling factor, explaining the k2 relationship.
For instance, take two squares where the side of one is twice as long as that of the other. The area of the larger square will then be four times that of the smaller one.
A Concrete Example
Let’s consider two similar squares for this example.
One square has sides 2 units in length, while the other has sides 4 units long.
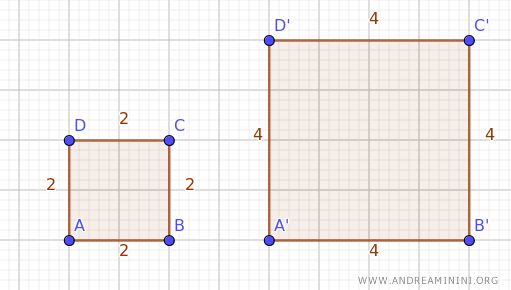
The scale factor between the squares is k=2, indicating that the sides of one square are twice as long as those of the other.
$$ k = \frac{\overline{A'B'}}{\overline{AB}} = \frac{4}{2} = 2 $$
Now, let's calculate the areas of both squares.
$$ A = \overline{AB} \cdot \overline{BC} = 2 \times 2 = 4 $$
$$ A' = \overline{A'B'} \cdot \overline{B'C'} = 4 \times 4 = 16 $$
Therefore, the area of the larger square is exactly four times the area of the smaller square.
Proof
Consider two similar polygons, such as squares.
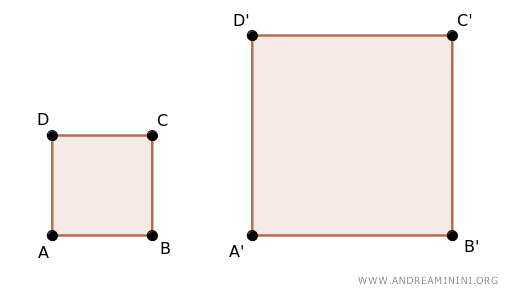
As these are similar polygons, all their sides are proportional, maintaining the same scale factor, k.
$$ \frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{B'C'}}{\overline{BC}} = k $$
Let's denote segment AB as the base (b) and segment BC as the height (h) of the polygon.
$$ \frac{\overline{b'}}{\overline{b}} = \frac{\overline{h'}}{\overline{h}} = k $$
This implies
$$ \frac{\overline{b'}}{\overline{b}} = k $$
$$ \frac{\overline{h'}}{\overline{h}} = k $$
From here, we can find the values of b' and h'.
$$ b' = k \cdot b $$
$$ h' = k \cdot h $$
Next, we calculate the area of the second square:
$$ A' = b' \cdot h' $$
Substituting the expressions for b' and h':
$$ A' = (b \cdot k) \cdot (h \cdot k) $$
$$ A' = b \cdot h \cdot k^2 $$
Since the product of the base and height, A=b·h, is the area of the first square,
$$ A' = A \cdot k^2 $$
This demonstrates that the area ratio between similar polygons is the square of their scale factor.
$$ \frac{A'}{A} = k^2 $$
And this principle applies to any polygon, not just squares. The logical reasoning remains the same whether dealing with triangles or any other shapes.
And there you have it.
