Chord Proportionality Theorem in a Circle
When two chords intersect within a circle, the segments formed on each chord create a proportion where the segments of one chord act as the means, and those on the other chord act as the extremes of the proportion.
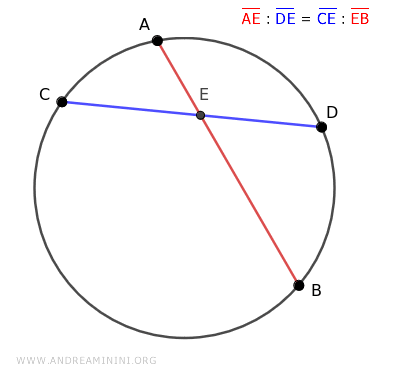
It doesn't matter which chord I choose to represent the extremes and which for the means, the proportion is still satisfied.
This is a similarity characteristic of circles.
Note. In a proportion, the means are the inner/central terms, while the extremes are the outer terms.
A Practical Example
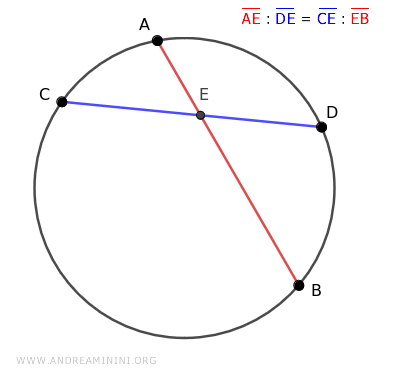
Let's take, for example, a circle with two intersecting chords AB and CD at point E inside the circle.
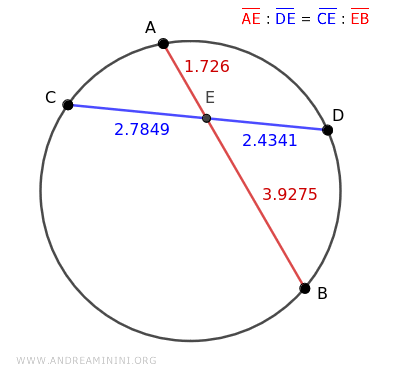
According to the chord theorem, the segments of one chord are the proportional means while those of the other chord are the proportional extremes.
$$ \overline{AE} : \overline{DE} = \overline{CE} : \overline{EB} $$
In this case, the means of the proportion are the segments of the blue chord CD, while the extremes are those of the red chord AB.
I substitute the lengths of the segments.
$$ 1.726 : 2.4341 = 2.7849 : 3.9275 $$
Calculating both ratios yields the same quotient.
$$ 0.709 = 0.709 $$
The proportion is satisfied.
Note. Obviously, reversing the proportion would yield the same result. For example, if I took the segments of the red chord AB as the proportional means and those of the chord CD as the proportional extremes, the proportion would still be satisfied. $$ \overline{DE} : \overline{AE} = \overline{EB} : \overline{CE} $$ $$ 2.4341 : 1.726 = 3.9275 : 2.7849 $$ $$ 1.41 : 1.41 $$
Proof
Consider a circle.
I draw two intersecting chords AB and CD inside the circle at point E.
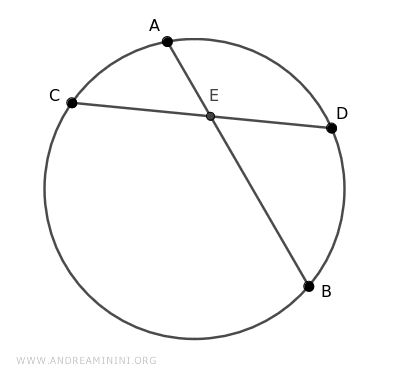
I add two segments AC and BD that connect the ends of the chords.
This forms two triangles, ACE and BDE.
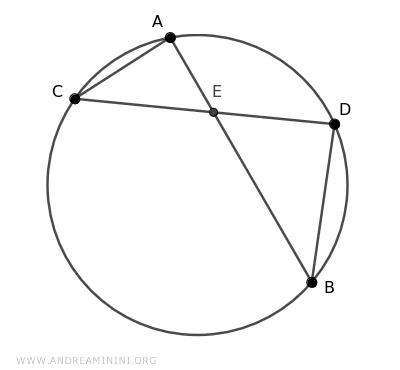
These two triangles share a congruent angle α≅α' at vertex E because α and α' are opposite angles at the vertex.
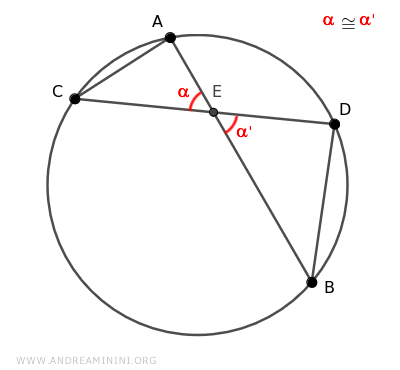
They also share another congruent angle β≅β', because angles β and β' are inscribed angles that subtend the same arc of the circle AD.
Therefore, by the theorem of inscribed angles, these angles are congruent.
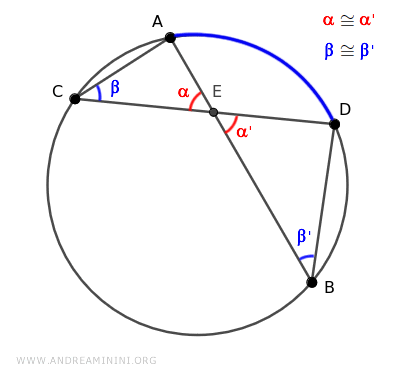
Consequently, by the first criterion of triangle similarity, triangles ACE and BDE are similar because they have two congruent angles α≅α' and β≅β'.
Being similar, triangles ACE and BDE have sides in proportion.
$$ \overline{AC} : \overline{BD} = \overline{AE} : \overline{DE} = \overline{CE} : \overline{EB} $$
Note. To find the corresponding sides, just look at the side opposite the congruent angles in the two triangles. For instance, knowing that α≅α' are congruent, the side opposite angle α in triangle ACE is side AC, while the side opposite angle α' in triangle BDE is side BD. Thus, AC and BD are corresponding sides of the two triangles.
The proportion I've just established confirms the initial theorem.
$$ \overline{AE} : \overline{DE} = \overline{CE} : \overline{EB} $$
The segments of one chord DE and CE are the means while the segments of the other chord AE and EB are the extremes of a proportion.
And so on.
