Circle Chords
A chord is a straight line segment connecting two distinct points on the circumference of a circle.
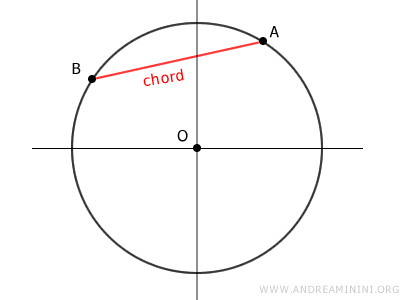
The diameter is a unique type of chord, being the longest possible one within a circle.
Contrary to the diameter, all other chords do not intersect the circle's center.
More broadly, a chord can be defined as a line segment whose ends touch two different points on a curve, such as a circle, an ellipse, or a hyperbola, or on opposite sides of a polygon. It's important to note that chords may have different properties depending on the curve they are part of.
Chords split the circle into two arcs.
This leads to saying that a chord subtends the two arcs, or put another way, each arc is subtended by the chord.
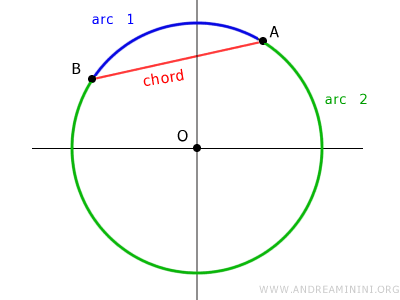
Thus, to indicate which arc of a chord I am referring to, adding a third point on the arc or adopting a convention (for example, moving in a clockwise direction between the endpoints) is necessary.
The straight line that contains a chord is known as a secant line.
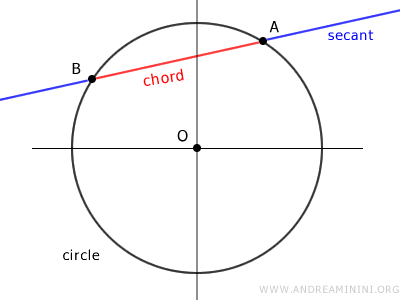
A chord, together with its corresponding arc, defines a finite area known as a segment of a circle, or simply a curve segment if part of any curve.
Insights
Insights and properties of circle chords
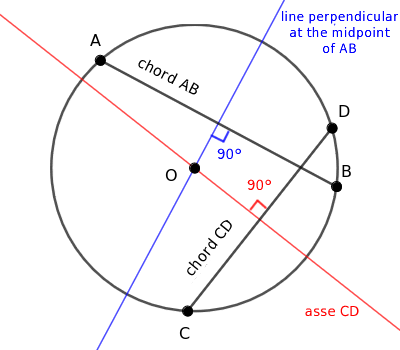
- Any chord's perpendicular bisector passes through the circle's center
Taking any chord with endpoints A and B on the circle, its perpendicular bisector - the line perpendicular at the midpoint - invariably crosses the circle's center.
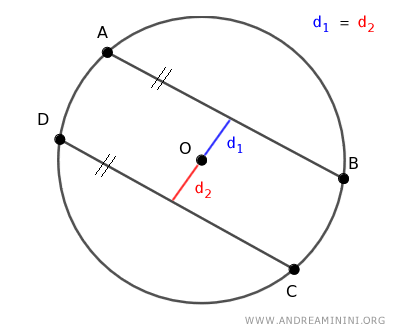
- Two chords are congruent if and only if their distance from the circle's center is the same
To be congruent, two chords AB and CD must share the same distance from the circle's center O, meaning d1=d2.
- Chord Theorem
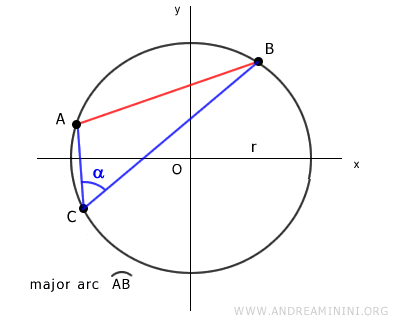
The length of a circle's chord AB, with radius r, equals twice the radius times the sine of one of the subtended angles α at the circle. $$ AB = 2r \sin \alpha $$
And the list goes on.
