Inscribed Angle Theorem

Within any circle, the size of an inscribed angle is always half the size of its subtended arc.

Put simply, if you have an inscribed angle that subtends an arc of α degrees, then the angle itself will be α/2 degrees in measure.

This principle applies to any arc and inscribed angle within a circle, not just semicircles.

A Hands-on Example

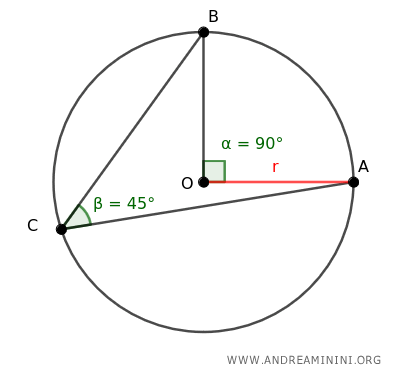
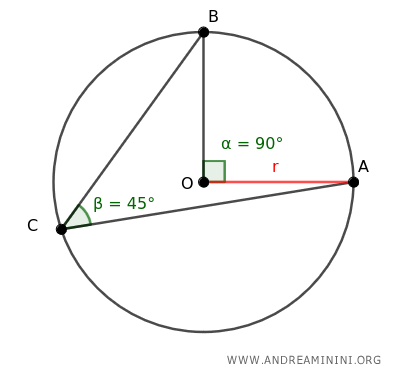
Imagine a circle with center O and a radius of r.

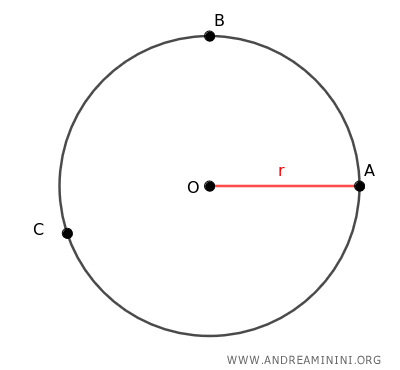
Take any three distinct points A, B, and C on the circle.

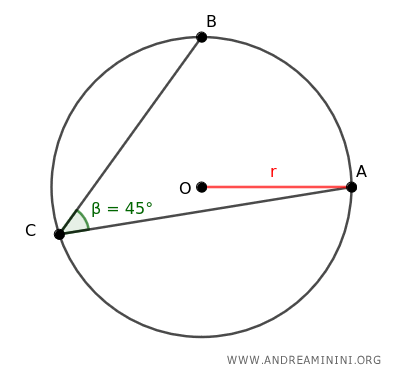
Draw segments BC and AC, creating the inscribed angle ∠ACB within the circle.

In this scenario, angle ACB measures 45°.

According to the Inscribed Angle Theorem, an inscribed angle's measure is half that of the arc it subtends.

Here, the arc in question is the segment AB of the circle.

Draw segments OA and OB to determine the central angle ∠AOB that subtends arc AB.

The central angle ∠AOB, subtending arc AB, measures 90°, which is twice that of the inscribed angle (45°).

The Proof

Let's consider a circle with center O and three points, A, B, C, on the circumference.

Points A and B on the circumference form the inscribed angle ∠ACB.

 

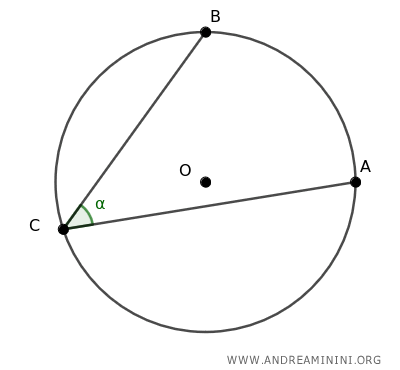
Next, I draw segments OA and OB.

The central angle ∠AOB spans the arc AB.

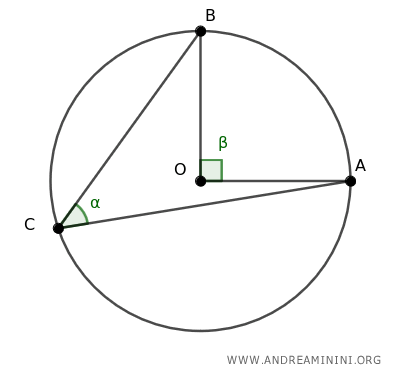
I also draw segment OC.

The triangles OAC and OBC are both isosceles since OA and OC are radii of the same circle, as are OB and OC.

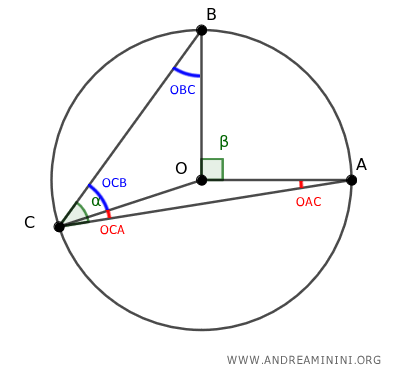
Knowing that the base angles of isosceles triangles are congruent, it follows that ∠OCA≡∠OAC and ∠OCB≡∠OBC.

The inscribed angle ∠ACB is the sum of angles ∠OCA and ∠OCB.

$$ ∠ACB = ∠OCA + ∠OCB $$

Extending segment OC to point D creates diameter CD of the circle.

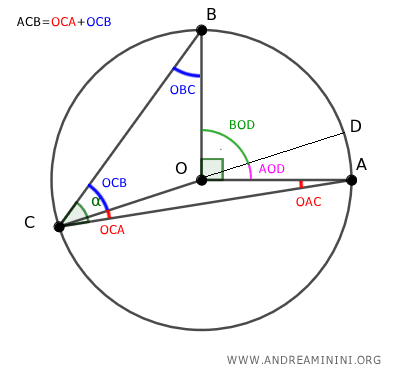
The angle ∠AOD acts as an exterior angle to triangle OAC. According to the Exterior Angle Theorem, it is equal to the sum of the non-adjacent internal angles ∠OCA and ∠OAC within triangle OAC.

$$ ∠AOD = ∠OCA + ∠OAC $$

With ∠OCA being congruent to ∠OAC, it simplifies to ∠AOD = 2 × ∠OCA.

$$ ∠AOD = 2 × ∠OCA $$

In a similar vein, angle ∠BOD serves as an exterior angle to triangle OBC. Again, by the Exterior Angle Theorem, it is equivalent to the sum of the non-adjacent internal angles ∠OBC and ∠OCB of triangle OBC.

$$ ∠BOD = ∠OBC + ∠OCB $$

Given that ∠OBC matches ∠OCB in measure, we can conclude ∠BOD = 2 × ∠OCB.

$$ ∠BOD = 2 × ∠OCB $$

Considering that angle ∠AOB is the aggregate of angles ∠AOD and ∠BOD, we find:

$$ ∠AOB = ∠AOD + ∠BOD $$

Given ∠AOD = 2 × ∠OCA and ∠BOD = 2 × ∠OCB, it follows that:

$$ ∠AOB = 2 × ∠OCA + 2 × ∠OCB $$

$$ ∠AOB = 2 × ( ∠OCA + ∠OCB ) $$

Recognizing ∠OCA + ∠OCB as ∠ACB allows us to state:

$$ ∠AOB = 2 × ∠ACB $$

This elegantly proves that the inscribed angle ∠ACB is exactly half the measure of the arc ∠AOB it subtends.

$$ \frac{ ∠AOB }{2} = ∠ACB $$

And so the story goes.