Intersecting Circles

Two circles are said to be intersecting when they share exactly two points.

It’s a geometric fact that circles cannot intersect at more than two points because any three points can only belong to a single unique circle.

Therefore, sharing three points would mean that the circles are essentially the same circle.

The Intersecting Circles Theorem

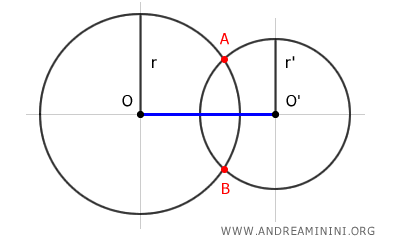
For two circles to intersect, the distance between their centers must be less than the sum of their radii yet greater than the difference between their radii. $$ | r-r' | < OO' < r+r' $$

Proof

The proof involves drawing the line OO' that connects the centers of the two circles and extending each circle's radius to a shared intersecting point, say point A.

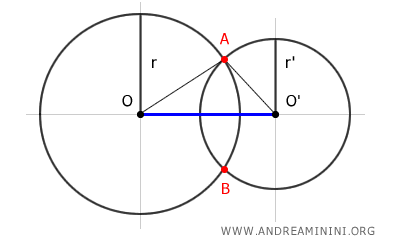
This construction forms a triangle, OO'A.

By the triangle inequality theorem, the length of any side of a triangle is less than the sum and more than the difference of the lengths of the other two sides.

Hence, the distance OO' between the centers must be less than the combined radii of the two circles (r+r') and more than their difference (r-r').

How to Find the Points of Intersection

To determine the points of intersection of two intersecting circles, we use analytical geometry.

Consider two circles with centers at \((x_1, y_1)\) and \((x_2, y_2)\) and radii \(r_1\) and \(r_2\):

The equations of the two circles are:

\[ (x - x_1)^2 + (y - y_1)^2 = r_1^2 \]

\[ (x - x_2)^2 + (y - y_2)^2 = r_2^2 \]

Here are the general steps to find the points of intersection of two circles:

1. Set up a system of equations with the circle equations and solve it step-by-step: \[ \begin{cases} x^2 + y^2 - 2x_1x - 2y_1y + x_1^2 + y_1^2 = r_1^2 \\ x^2 + y^2 - 2x_2x - 2y_2y + x_2^2 + y_2^2 = r_2^2 \end{cases} \]
2. Subtract one equation from the other to eliminate the \(x^2\) and \(y^2\) terms, making one equation linear.
3. Solve the linear equation for one variable, for example, \(y\) in terms of \(x\).
4. Substitute this expression for \(y\) into one of the original circle equations (usually the simpler one).
5. Solve the resulting quadratic equation for \(x\) using the quadratic formula: \[ ax^2 + bx + c = 0 \] \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
6. Once you have the \(x\) values, substitute them back into the expression for \(y\) to find the corresponding \(y\) values.

These steps will give you the coordinates \((x, y)\) of the intersection points of the circles.

Example

Let's consider two intersecting circles with the following equations:

$$ C_1 : \ x^2 + y^2 = 25 $$

$$ C_2 : \ (x - 4)^2 + (y - 3)^2 = 16 $$

The first equation represents a circle centered at the origin O(0, 0) with a radius of \( r_1 = 5 \).

The second equation represents a circle centered at (4, 3) with a radius of \( r_2 = 4 \).

The Euclidean distance between the centers, OO', with coordinates (x₁, y₁) and (x₂, y₂), is \( d = 4 \).

$$ d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$

$$ d = \sqrt{(0 - 4)^2 + (0 - 3)^2} $$

$$ d = \sqrt{16 + 9} = \sqrt{25} = 5 $$

According to the theorem, when two circles intersect, the distance between their centers (d=5) is less than the sum of the radii and greater than the absolute value of the difference of the radii.

$$ | r_1 - r_2 | < d < r_1 + r_2 $$

$$ | 5 - 4 | < 5 < 5 + 4 $$

$$ 1 < 5 < 9 $$

Therefore, the two circles intersect.

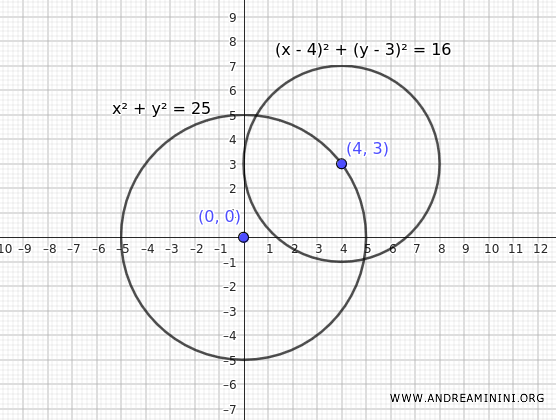
What are the points of intersection of the two circles?

First, expand the second equation:

\[ (x - 4)^2 + (y - 3)^2 = 16 \]

\[ x^2 - 8x + 16 + y^2 - 6y + 9 = 16 \]

\[ x^2 + y^2 - 8x - 6y + 25 = 16 \]

\[ x^2 + y^2 - 8x - 6y + 9 = 0 \]

Now, set up the system of equations:

\[ \begin{cases} x^2 + y^2 = 25 \\ x^2 + y^2 - 8x - 6y + 9 = 0 \end{cases} \]

Subtract the first equation from the second:

\[ \begin{cases} x^2 + y^2 = 25 \\ (x^2 + y^2 - 8x - 6y + 9) - (x^2 + y^2) = 0 - 25 \end{cases} \]

\[ \begin{cases} x^2 + y^2 = 25 \\ -8x - 6y + 9 = -25 \end{cases} \]

\[ \begin{cases} x^2 + y^2 = 25 \\ -8x - 6y = -34 \end{cases} \]

Multiply both sides of the second equation by -1 to simplify:

\[ \begin{cases} x^2 + y^2 = 25 \\ 8x + 6y = 34 \end{cases} \]

\[ \begin{cases} x^2 + y^2 = 25 \\ 4x + 3y = 17 \end{cases} \]

Now, solve for \( y \) in terms of \( x \):

\[ \begin{cases} x^2 + y^2 = 25 \\ y = \frac{17 - 4x}{3} \end{cases} \]

Substitute this expression for \( y \) into the first equation:

\[ \begin{cases} x^2 + \left( \frac{17 - 4x}{3} \right)^2 = 25 \\ y = \frac{17 - 4x}{3} \end{cases} \]

\[ x^2 + \frac{(17 - 4x)^2}{9} = 25 \]

Multiply through by 9 to clear the fraction:

\[ 9x^2 + (17 - 4x)^2 = 225 \]

Expand and simplify:

\[ 9x^2 + 289 - 136x + 16x^2 = 225 \]

\[ 25x^2 - 136x + 64 = 0 \]

Solve the quadratic equation:

\[ x = \frac{136 \pm \sqrt{136^2 - 4 \cdot 25 \cdot 64}}{2 \cdot 25} \]

\[ x = \frac{136 \pm \sqrt{18496 - 6400}}{50} \]

\[ x = \frac{136 \pm \sqrt{12096}}{50} \]

\[ x = \frac{136 \pm 110}{50} \]

Thus, the x-values of the points of intersection are:

\[ x = \frac{136 + 110}{50} = \frac{246}{50} = 4.92 \]

\[ x = \frac{136 - 110}{50} = \frac{26}{50} = 0.52 \]

Finally, substitute these x-values back into the expression for \( y \):

$$ y = \frac{17 - 4x}{3} $$

• For \( x = 4.92 \): \[ y = \frac{17 - 4 \cdot 4.92}{3} = \frac{17 - 19.68}{3} = \frac{-2.68}{3} = -0.893 \]
• For \( x = 0.52 \): \[ y = \frac{17 - 4 \cdot 0.52}{3} = \ frac{17 - 2.08}{3} = \frac{14.92}{3} = 4.973 \]

Therefore, the points of intersection are approximately \((4.92, -0.893)\) and \((0.52, 4.973)\).

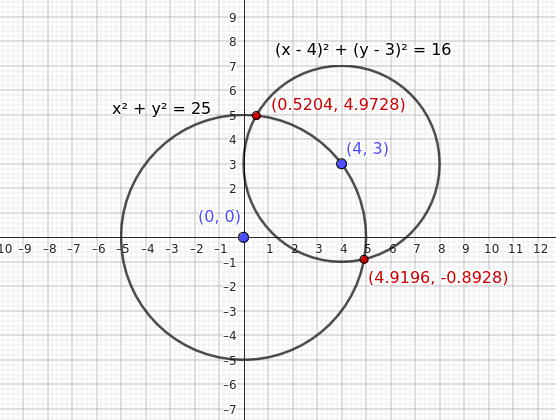
These are the points of intersection of the two intersecting circles.

Key Insights on Intersecting Circles

Some interesting observations on intersecting circles include:

• The chord AB that connects the intersection points of the circles stands perpendicular to the line OO' joining the centers of the two circles.
  

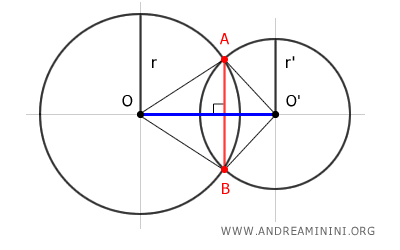
  Here's why: Take two intersecting circles at points A and B. Connect their centers, O and O', with a line OO'. Draw lines OA, OB, O'A, and O'B. Segments OA and OB are congruent, as they are both radii of the first circle, and likewise, O'A and O'B are congruent, being radii of the second circle. $$ \overline{OA} \cong \overline{OB} $$ $$ \overline{O'A} \cong \overline{O'B} $$ This means that points A and B are equidistant from both centers O and O', establishing that chord AB is perpendicular to line OO'.