Tangent and polar line formulas

Doubling formulas allow us to express the coordinates of a point and the parameters of a curve in such a way that we obtain the polar equation.

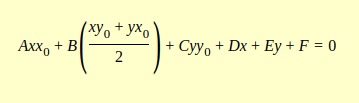
For a conic curve represented in Cartesian coordinates by the general equation:

$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$

and a point \( P(x_0, y_0) \), the polar equation of \( P \) with respect to this conic is given by:

$$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$

We are dealing with conic curves, such as circles, ellipses, parabolas, and hyperbolas, and a point external to these curves.

The simplest case is a circle \( x^2 + y^2 + ax + by + c = 0 \).

The concept of the polar line was introduced during the development of analytic and projective geometry in the 19th century. Mathematicians like Poncelet and Chasles made significant contributions to these theories.

If we have a conic curve like a circle and we take a point P outside the conic, we can define a line called the "polar line" of point P with respect to the conic.

The polar line is the red line that intersects the circle at the tangency points A and B, which belong to the tangent lines passing through the external point P.

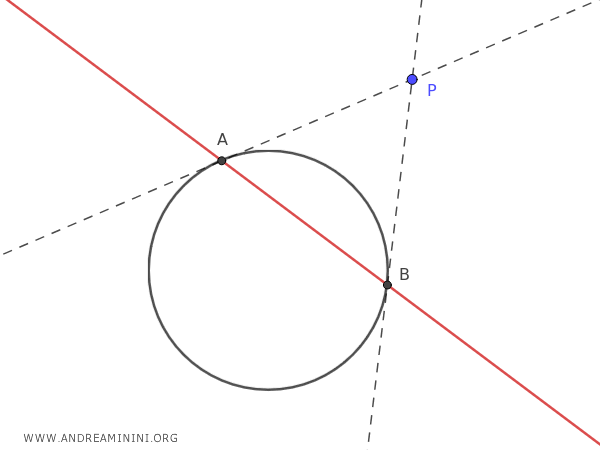
In other words, the polar line is a line whose intersection points A and B on the circle coincide with the tangency points of the tangents passing through the external point P.

In the special case where point P lies on the circle, the result coincides with the tangent line.

Therefore, in this case, we obtain the tangent line equation.

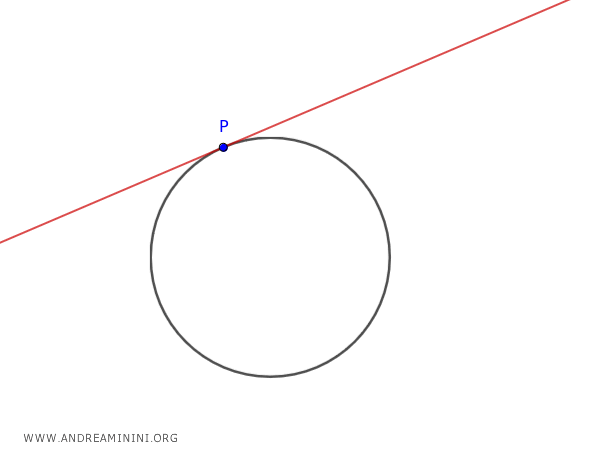
Thus, "doubling formulas" are equations that allow us to find the tangent or polar equation at a point P on the conic.

Note. The term "doubling" refers to the fact that, considering a point on the conic, we can think of this point as the result of the coexistence of two infinitely close intersection points (almost coinciding) on the conic, from which the tangent touches the conic at that specific point.

Using the implicit form of the conic, we can derive the following expressions:

Symmetric representation:

$$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey = 0 $$

Doubling formulas for conics:

For a circle \( x^2 + y^2 + 2gx + 2fy + c = 0 \):

$$ xx_0 + yy_0 + g(x + x_0) + f(y + y_0) + c = 0 $$

For a parabola \( y^2 = 4ax \):

$$ yy_0 = 2a(x + x_0) $$

What are they used for? Doubling formulas are used to find the equations of tangents, normals, and polars related to algebraic curves. For example, I can use the doubling formula on a circle to find the equation of the tangent line at point P on the circle. 

Practical Example

Let me provide a practical example to better illustrate the concept of doubling formulas and the polar line.

Consider a circle centered at the origin with a radius \( r = 5 \), so the equation is:

$$ x^2 + y^2 = 25 $$

Take a point on the circle \( P(3, 4) \).

Note. To verify that this point lies on the circle, just substitute the point coordinates \( x=3 \) and \( y=4 \) into the circle equation $$ x^2 + y^2 = 25 $$ $$ 3^2 + 4^2 = 25 $$ $$ 9+16 =25 $$ $$ 25=25 $$ The identity is confirmed.

Use the formula \( xx_0 + yy_0 = r^2 \) to find the tangent line equation at point \( P(3, 4) \).

Substitute \( x_0 = 3 \), \( y_0 = 4 \), and \( r^2 = 25 \) into the formula:

$$ x \cdot 3 + y \cdot 4 = 25 $$

$$ 3x + 4y = 25 $$

This is the equation of the tangent line to the circle at point \( P(3, 4) \).

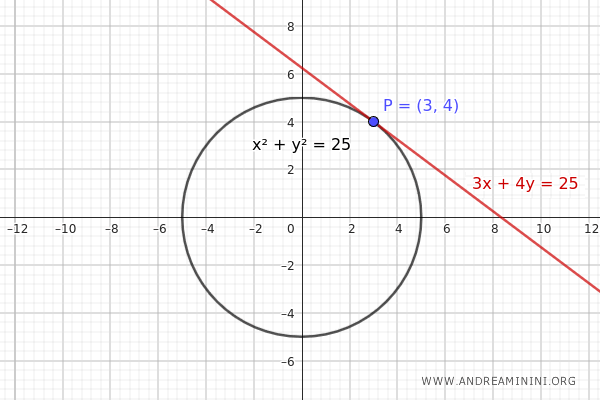
Now, let's find the polar line equation with respect to an external point \( Q \) outside the circle \( x^2 + y^2 = 25 \), for example, \( Q(6, 8) \).

The polar of point \( Q \) with respect to the circle \( x^2 + y^2 = 25 \) is the line that represents all the tangency points of the tangents passing through point \( Q \).

We use the formula:

$$ xx_0 + yy_0 = r^2 $$

But in this case, \( (x_0, y_0) \) is the point \( Q(6, 8) \), and the polar line will be:

$$ x \cdot 6 + y \cdot 8 = 25 $$

$$ 6x + 8y = 25 $$

This line represents the polar of point \( Q(6, 8) \) with respect to the circle \( x^2 + y^2 = 25 \).

The intersection points of the polar line coincide with the tangency points A and B on the circle of the two tangents that also pass through the external point \( Q(6, 8) \).

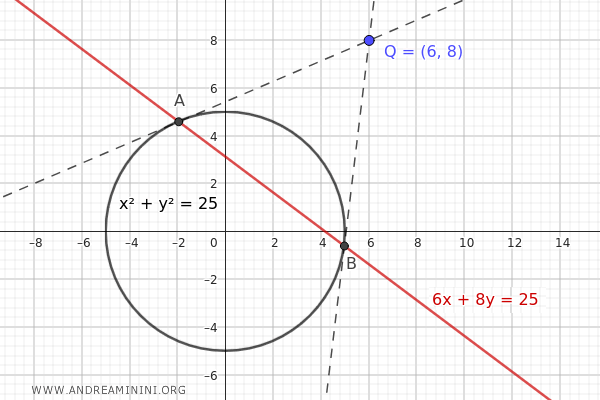
In conclusion, in this practical example, I used the doubling formula to find the equation of the tangent to a circle and to determine the polar of a point outside the circle.

Observations

Some observations and notes about the doubling formulas:

• The polar of a point with respect to a conic can be seen as the set of tangency points of the tangents to the conic passing through that point.
• If \( P \) is a point outside a conic, its polar with respect to that conic will be the tangent line to the conic at the contact points of the tangents from \( P \).
• If point \( P \) lies on the polar of point \( Q \), then \( Q \) lies on the polar of \( P \).

And so on.