Dandelin spheres

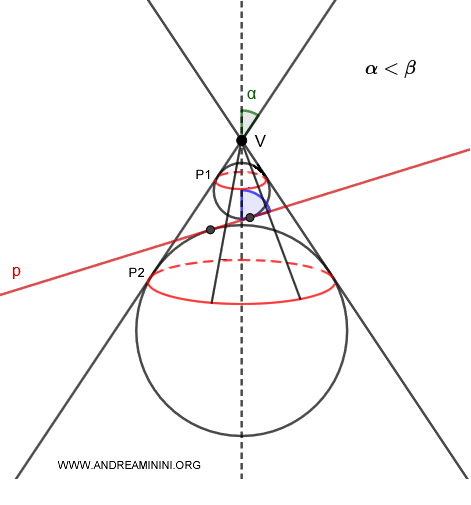
Dandelin spheres are spheres inscribed within a double-napped right circular cone, each tangent at a point $F$ on a secant plane $p$.

The secant plane $p$ does not pass through the vertex $V$ of the cone.

Depending on the cone's semi-aperture angle $ \alpha $ and the inclination angle $ \beta $ of the plane, there are three possible scenarios:

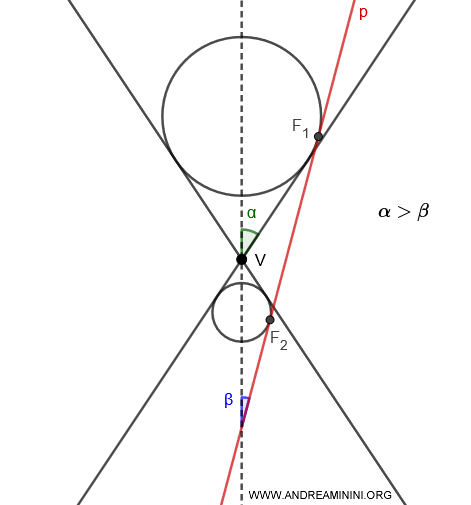
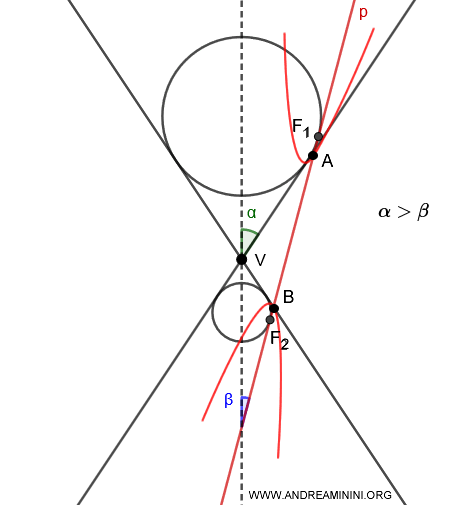
• If $ \alpha > \beta $, two Dandelin spheres are inscribed, one in each nappe of the cone, and they are tangent to the plane at points $F_1$ and $F_2$.
  
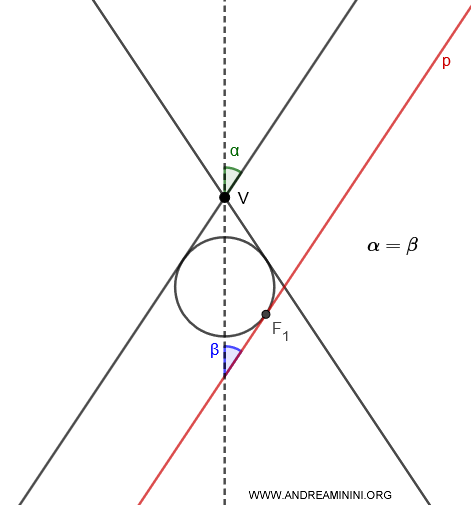
• If $ \alpha = \beta $, there is a single Dandelin sphere inscribed in the nappe intersected by the plane $p$.
  
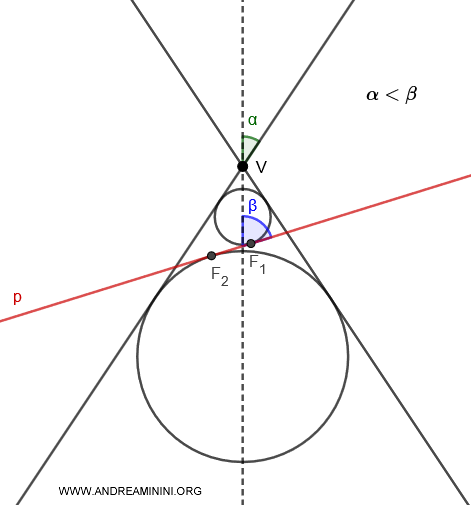
• If $ \alpha < \beta $, two Dandelin spheres are inscribed within the same nappe intersected by the plane $p$, and they are tangent to the plane at points $F_1$ and $F_2$.
  

This simplified side view of the cone and plane is used to clarify the concept.

In reality, Dandelin spheres are tangent to all the generating lines of the circular cone, and the points of tangency form a circle on a plane perpendicular to the cone's axis.

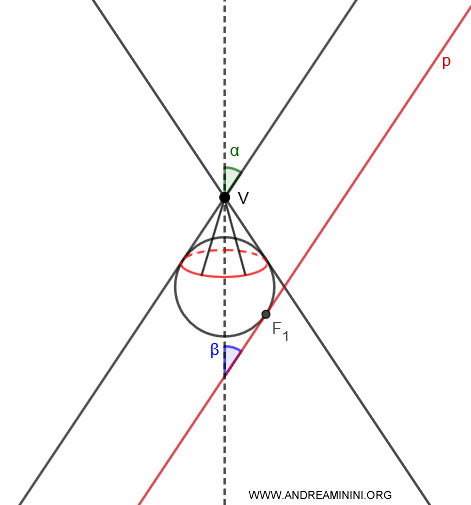
Note. The circles are positioned on planes that are perpendicular (90°) to the axis of symmetry. They do not lie on the axis that intersects the cone, which is instead tilted at an angle of β.

When two Dandelin spheres are tangent to the generating lines of the same cone, the distance between the points of tangency $P_1$ and $P_2$ remains constant along each generating line.

 

Dandelin spheres, introduced by mathematician Germinal Pierre Dandelin in 1822, are a geometric concept used to demonstrate certain properties of conic sections (ellipses, parabolas, and hyperbolas).

Conic sections (ellipse, parabola, hyperbola) are the curves formed by the intersection of this cone with a plane.

• Ellipse: When the plane intersects a side of the cone, forming an ellipse, two inscribed spheres touch the plane at two distinct points. These points are the foci of the ellipse.
• Parabola: If the plane is parallel to a generator of the cone, there is a single inscribed sphere that touches the plane at one point—this point is the focus of the parabola.
• Hyperbola: When the plane intersects both sides of the cone, two inscribed spheres touch the plane at different points, which are the foci of the hyperbola.

Thus, Dandelin spheres offer a geometric method for proving some fundamental properties of conic sections, which are typically addressed using algebraic methods.

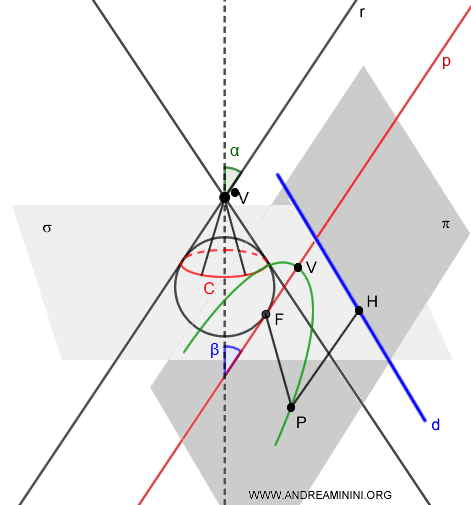
The eccentricity of a conic section is determined by the half-angle $ \alpha $ of the cone and the angle $ \beta $ at which the intersecting plane is inclined.

$$ e = \frac{ \overline{PF} }{ \overline{PH} } = \frac{\cos \alpha }{ \cos \beta} $$

In this equation, $ \overline{PF} $ is the distance from a point $ P $ on the conic to the focus $ F $, and $ \overline{PH} $ is the distance from point $ P $ to the directrix $ d $.

The directrix $ d $ is formed by the intersection of the plane $ \pi $ with the plane $ \sigma $, which is perpendicular to the axis of symmetry of the cone.

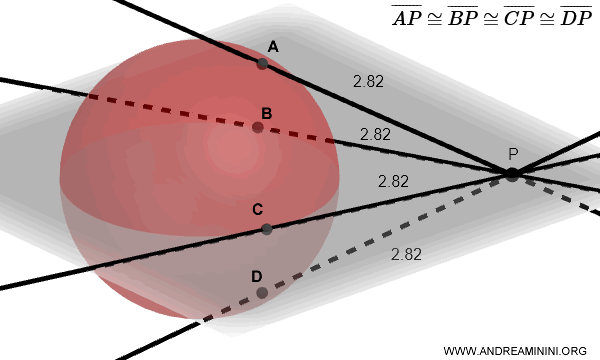
Note: A particularly useful theorem involving spheres, often used in the proofs of Dandelin's theorems, is as follows: all tangent segments drawn from an external point P to a sphere are congruent, meaning $ \overline{AP} \cong \overline{BP} \cong \overline{CP} \cong \overline{DP} $

Dandelin's Theorem for the Ellipse

When a plane intersects a single sheet of a cone and two inscribed spheres touch the plane at distinct points, $F_1$ and $F_2$, these points are the foci of the ellipse formed on the plane. The vertices of the ellipse are at points A and B.

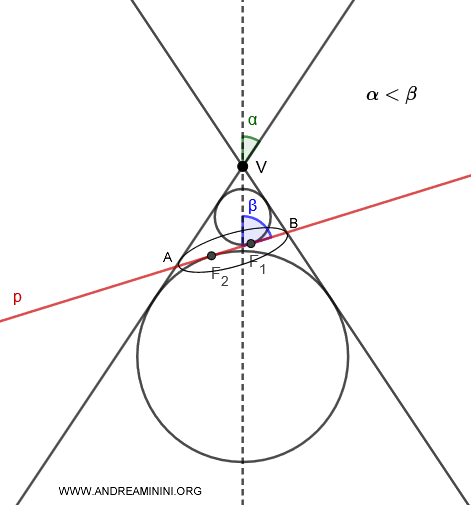
For any point P on the ellipse, the sum of the distances $ \overline{PF_1} $ and $ \overline{PF_2} $ is constant and equal to the length of segment AB: $$ \overline{PF_1} + \overline{PF_2} = \overline{AB} $$

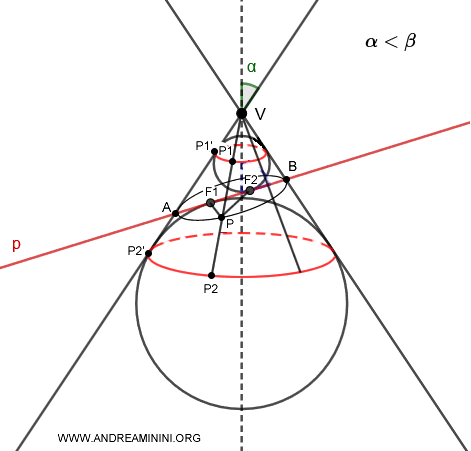
Proof

The segments connecting the points where the cone's generating lines intersect the two circles (which are perpendicular to the axis of symmetry) are congruent because they originate from a single external point, V, outside the spheres.

$$ \overline{P_1P_2} \cong \overline{P_1'P_2'} $$

Each segment between the two circles intersects the ellipse and is composed of the sum of two segments:

$$ \overline{P_1P_2} = \overline{P_1P} + \overline{PP_2} $$

At any point P on the ellipse, the sum of the distances to the foci is constant:

$$ \overline{PF_1} + \overline{PF_2} = k $$

Now, let's consider P as the vertex A or B of the ellipse:

$$ \overline{AF_1} + \overline{AF_2} = \overline{BF_1} + \overline{BF_2} = k $$

We need to determine the value of the constant k.

Since segment AB can be expressed as $ \overline{AB} = \overline{AF_2} + \overline{BF_2} $, we deduce that $ \overline{AF_2} = \overline{AB} - \overline{BF_2} $.

$$ \overline{AF_1} + \overline{AF_2} = \overline{BF_1} + \overline{BF_2} $$

$$ \overline{AF_1} + (\overline{AB} - \overline{BF_2}) = \overline{BF_1} + \overline{BF_2} $$

$$ \overline{AF_1} + \overline{AB} - \overline{BF_2} = \overline{BF_1} + \overline{BF_2} $$

$$ \overline{AF_1} + \overline{AB} - \overline{BF_1} = 2\overline{BF_2} $$

The segment $ \overline{AB} - \overline{BF_1} = \overline{AF_1} $

$$ \overline{AF_1} + (\overline{AB} - \overline{BF_1}) = 2\overline{BF_2} $$

$$ \overline{AF_1} + \overline{AF_1} = 2\overline{BF_2} $$

$$ 2 \overline{AF_1} = 2\overline{BF_2} $$

Dividing both sides by two:

$$ \overline{AF_1} = \overline{BF_2} $$

This shows that the segments $ \overline{AF_1} = \overline{BF_2} $ are congruent.

Returning to the previous equation where $ k $ is still unknown:

$$ \overline{AF_1} + \overline{AF_2} = \overline{BF_1} + \overline{BF_2} = k $$

We know that $ \overline{AF_2} = \overline{AF_1} + \overline{F_1F_2} $:

$$ \overline{AF_1} + (\overline{AF_1} + \overline{F_1F_2}) = \overline{BF_1} + \overline{BF_2} = k $$

$$ \overline{AF_1} + \overline{AF_1} + \overline{F_1F_2} = \overline{BF_1} + \overline{BF_2} = k $$

Since $ \overline{AF_1} = \overline{BF_2} $, we have:

$$ \overline{AF_1} + \overline{BF_2} + \overline{F_1F_2} = \overline{BF_1} + \overline{BF_2} = k $$

The sum of the segments $ \overline{AF_1} + \overline{F_1F_2} + \overline{BF_2} = \overline{AB} $

$$ \overline{AB} = \overline{BF_1} + \overline{BF_2} = k $$

Therefore, the constant k is equal to the length of segment AB.

$$ k = \overline{AB} $$

Since the constant $ k $ is the same for any point $ P $, we've shown that:

$$ \overline{PF_1} + \overline{PF_2} = \overline{AB} $$

This is exactly what happens at every point on an ellipse.

Dandelin's Theorem for Parabolas

When a secant plane \( \pi \) is parallel to a generating line \( r \) of a cone, there is exactly one sphere inscribed within the cone that touches the plane at a single point \( F \). This point \( F \) corresponds to the focus of the parabola traced on the plane \( \pi \).

The directrix \( d \) of the parabola is found by intersecting the secant plane \( \pi \) with a plane \( \sigma \) perpendicular to the cone's axis, which contains the circle \( C \), formed by the points of tangency between the sphere and the cone.

For any point \( P \) on the parabola, the following equation holds:

$$ \overline{PH} = \overline{PF} $$

Here, \( \overline{PH} \) is the distance from point \( P \) to its projection \( H \) on the directrix, and \( \overline{PF} \) is the distance from \( P \) to the focus \( F \).

This theorem provides a geometric proof that the definition of a parabola as the set of points equidistant from a fixed point (the focus) and a line (the directrix) can be derived from its conic construction.

Proof

Consider any point \( P \) on the parabola.

A generating line \( g \) of the cone passes through \( P \) and intersects the circle \( C \) at \( T \).

Now, imagine a circle \( C_2 \) on a plane perpendicular to the cone's axis of symmetry that passes through \( P \).

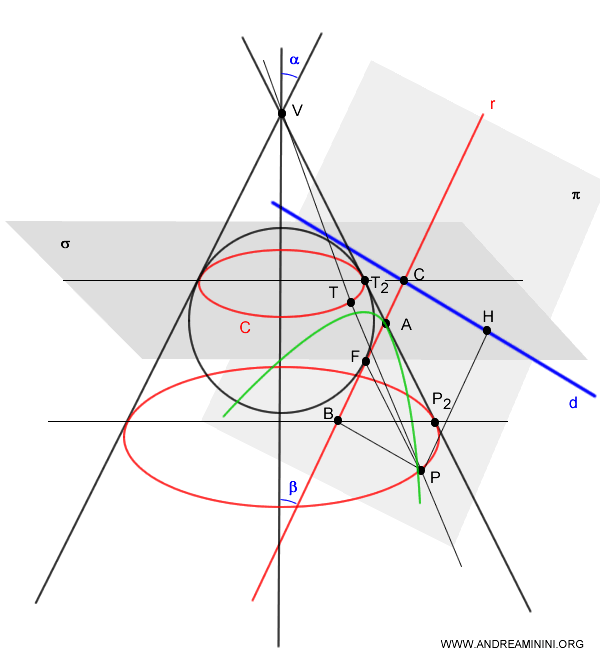
The segment \( \overline{PT} \) is congruent to the segment \( \overline{P_2T_2} \) because the circles \( C \) and \( C_2 \) are perpendicular to the cone's axis, and the generating lines all originate from the same point \( V \).

$$ \overline{PT} \cong \overline{P_2T_2} $$

Let \( B \) be the projection of point \( P \) onto the parabola's axis of symmetry \( p \), and \( H \) be the projection of \( P \) onto the directrix \( d \).

Thus, the quadrilateral \( CBPH \) forms a rectangle.

In a rectangle, opposite sides are congruent:

$$ \overline{BC} \cong \overline{PH} $$

$$ \overline{BP} \cong \overline{CH} $$

By the initial assumption, the semi-vertical angle \( \alpha \) of the cone is congruent to the angle \( \beta \) of the secant plane \( \pi \).

$$ \alpha \cong \beta $$

This makes the triangles \( ACT_2 \) and \( ABP_2 \) similar and isosceles.

From this, we conclude that the segments \( \overline{P_1T_1} \) and \( \overline{BC} \) are congruent:

$$ \overline{P_1T_1} \cong \overline{BC} $$

Since both \( \overline{PF} \) and \( \overline{PT} \) are tangents from the same point \( P \) to the sphere, they must be congruent:

$$ \overline{PF} \cong \overline{PT} $$

Given that \( \overline{PT} \cong \overline{P_1T_1} \) and \( \overline{P_1T_1} \cong \overline{BC} \), it follows that:

$$ \overline{PF} \cong \overline{BC} $$

And since \( \overline{BC} \cong \overline{PH} \) as opposite sides of a rectangle:

$$ \overline{PF} \cong \overline{PH} $$

This proves that for any point \( P \) on the parabola, the distance to the focus \( F \) is equal to the distance to its projection \( H \) on the directrix \( d \).

Note: Even when \( P \) is the vertex \( A \) of the parabola, the relation \( PF \cong PH \) still holds. Since triangle \( ACT_2 \) is isosceles, its oblique sides are congruent \( \overline{AC} \cong \overline{AT_2} \). Additionally, \( \overline{AT_2} \cong \overline{AF} \), as both segments originate from the same point \( A \) and are tangents to the sphere. Therefore, when \( P=A \) and its projection is \( H=C \), the relation \( AF \cong AC \), or \( PF \cong PH \), remains valid.

Dandelin's Theorem for the Hyperbola

When a plane intersects both nappes of a cone, two inscribed spheres are tangent to the intersecting plane. The points of tangency are the foci of the hyperbola.

For any point $ P $ on the hyperbola, the following relationship holds:

$$ | \overline{PF_1} - \overline{PF_2} | = \overline{AB} $$

Where $ A $ and $ B $ are the vertices of the hyperbola.

Proof

Consider a point $ P $ on the hyperbola, lying on the generating line $ g $ of the cone.

The generating line intersects the circles $ C_1 $ and $ C_2 $ of the inscribed spheres at points $ P_1 $ and $ P_2 $.

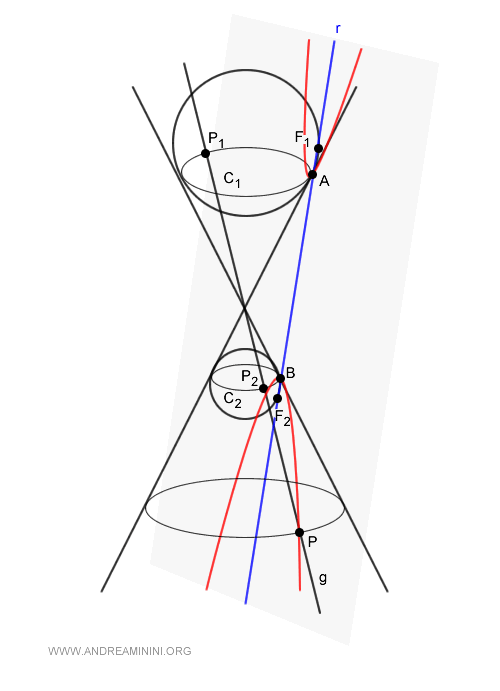
The segments $ \overline{PF_1} $ and $ \overline{PP_1} $ are congruent because they are tangent to the same sphere and originate from the same point $ P $.

$$ \overline{PF_1} \cong \overline{PP_1} $$

Similarly, the segments

$$ \overline{PF_2} \cong \overline{PP_2} $$

are also congruent. Therefore, the differences between them are equal:

$$ | \overline{PF_1} - \overline{PF_2} | = | \overline{PP_1} - \overline{PP_2} | $$

The difference $ | \overline{PP_1} - \overline{PP_2} | $ is the segment $ \overline{P_1P_2} $, which remains constant for any point on the circles $ C_1 $ or $ C_2 $.

$$ | \overline{PF_1} - \overline{PF_2} | = | \overline{PP_1} - \overline{PP_2} | = \overline{P_1P_2} $$

Now, consider $ P $ as the vertex $ A $ of the hyperbola:

$$ | \overline{AF_1} - \overline{AF_2} | = \overline{P_1P_2} $$

And then as the vertex $ B $ of the hyperbola:

$$ | \overline{BF_2} - \overline{BF_1} | = \overline{P_1P_2} $$

Both differences $ | \overline{AF_1} - \overline{AF_2} | $ and $ | \overline{BF_1} - \overline{BF_2} | $ are equal to $ \overline{P_1P_2} $:

$$ | \overline{AF_1} - \overline{AF_2} | = | \overline{BF_2} - \overline{BF_1} | $$

We know that $ \overline{AF_2} $ equals $ \overline{F_1F_2} - \overline{AF_1} $, and $ \overline{BF_1} $ equals $ \overline{F_1F_2} - \overline{BF_2} $:

$$ | \overline{AF_1} - (\overline{F_1F_2} - \overline{AF_1}) | = | \overline{BF_2} - (\overline{F_1F_2} - \overline{BF_2}) | $$

$$ | \overline{AF_1} - \overline{F_1F_2} + \overline{AF_1} | = | \overline{BF_2} - \overline{F_1F_2} + \overline{BF_2} | $$

$$ | 2 \overline{AF_1} - \overline{F_1F_2} | = | 2 \overline{BF_2} - \overline{F_1F_2} | $$

Simplifying by eliminating $ \overline{F_1F_2} $ from both sides:

$$ | 2 \overline{AF_1} | = | 2 \overline{BF_2} | $$

Knowing that segment lengths are always positive, we can drop the absolute values:

$$ 2 \overline{AF_1} = 2 \overline{BF_2} $$

Finally, dividing both sides by 2:

$$ \overline{AF_1} = \overline{BF_2} $$

With this equality established, we return to the original difference $ | \overline{AF_1} - \overline{AF_2} | $:

$$ | \overline{AF_1} - \overline{AF_2} | $$

Given that $ \overline{AF_1} = \overline{BF_2} $:

$$ | \overline{BF_2} - \overline{AF_2} | $$

We can rewrite the absolute difference by placing the longer segment first:

$$ | \overline{AF_2} - \overline{BF_2} | $$

This difference $ \overline{AF_2} - \overline{BF_2} $ is the segment $ \overline{AB} $:

$$ | \overline{AF_2} - \overline{BF_2} | = \overline{AB} $$

Therefore,

$$ | \overline{AF_1} - \overline{AF_2} | = | \overline{BF_2} - \overline{BF_1} | = \overline{AB} $$

This proves that for any point $ P $, the absolute difference between the distances to the foci is equal to the distance between the vertices of the hyperbola:

$$ | \overline{PF_1} - \overline{PF_2} | = \overline{AB} $$

And so forth.