Parabolas

A parabola is a second-order plane algebraic curve, defined as the set of all points equidistant from a fixed point called the focus (F) and a fixed line (d) called the directrix, which does not pass through the focus.

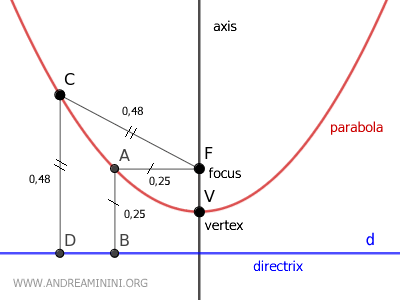
In other words, the points on the parabola form a geometric locus because they are equidistant from the focus (F) and the directrix (d) of the parabola.

The axis of the parabola is the line that passes through the focus and is perpendicular to the directrix.

The vertex of the parabola is the point where the axis intersects the parabola.

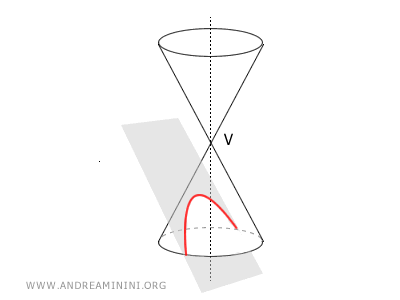
A parabola can also be defined as the surface (conic section) obtained by intersecting an infinite circular cone with a plane parallel to the cone's generating line.

 

Note: The parabola has various applications in physics, engineering, and other sciences. For example, in physics, it can describe the trajectory of a projectile in the absence of air resistance.

The Equation of a Parabola

The standard form of the equation of a parabola with its axis of symmetry parallel to the y-axis is:

$$ y = ax^2 + bx + c $$

Where a, b, and c are real constant coefficients with a not equal to zero (a ≠ 0).

Note: The width of the parabola depends on the absolute value of the coefficient "a". As the absolute value |a| increases, the parabola becomes narrower, and vice versa. The sign of the coefficient "a" also determines the direction of the parabola's opening. If a > 0, the parabola opens upwards (convex), if a < 0, it opens downwards (concave).

If the axis of symmetry is horizontal, the standard equation is:

$$ x = ay^2 + by + c $$

The main components of a parabola are:

• Focus
  The focus (F) is a fixed point inside the parabola. The coordinates of the focus are obtained as follows: $$ F \begin{pmatrix} - \frac{b}{2a} \ , \ \frac{1-Δ}{4a} \end{pmatrix} $$ where a, b, and c are the coefficients of the parabola's equation y = ax² + bx + c and the discriminant Δ = b² - 4ac.
• Directrix
  The directrix (d) is a fixed line outside the parabola. The equation of the directrix is: $$ y = - \frac{1 + Δ}{4a} $$
• Axis
  The axis is a line perpendicular to the directrix (d) passing through the focus (F) of the parabola. The axis of the parabola is also an axis of symmetry as it divides the parabola into two mirror-image halves. The equation of the axis is: $$ x = - \frac{b}{2a} $$
• Vertex
  The vertex (V) is the point where the parabola intersects the axis. At the vertex, the parabola reaches its maximum or minimum value depending on the sign of the coefficient "a" of the parabola's equation y = ax² + bx + c. The coordinates of the vertex are calculated as follows: $$ V \begin{pmatrix} - \frac{b}{2a} \ , \ - \frac{Δ}{4a} \end{pmatrix} $$

A Practical Example

Consider the equation of the following parabola:

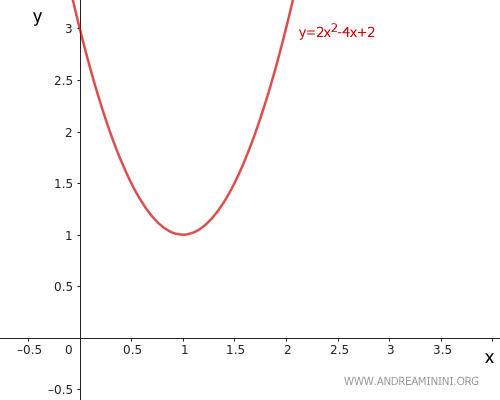
$$ y = 2x^2 - 4x + 3 $$

The real coefficients of the equation are a = 2, b = -4, and c = 3.

From the positive sign of the coefficient a = 2, we can immediately tell that the parabola opens upwards.

We use the formula to determine the directrix of the parabola:

$$ y = - \frac{1 + Δ}{4a} $$

Knowing that a = 2, b = -4, and c = 3, the discriminant Δ = b² - 4ac is as follows:

$$ Δ = b^2 - 4ac = (-4)^2 - 4 \cdot 2 \cdot 3 = 16 - 24 = -8 $$

Thus, the equation of the directrix is:

$$ y = - \frac{1 + Δ}{4a} = - \frac{1 - 8}{4 \cdot 2} = - \frac{-7}{8} = \frac{7}{8} $$

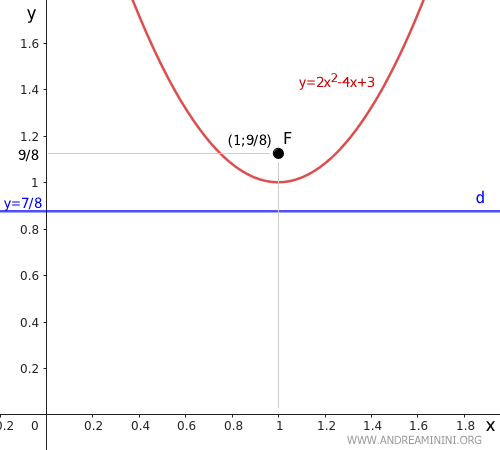
We add the directrix (d) y = 7/8 to the graph:

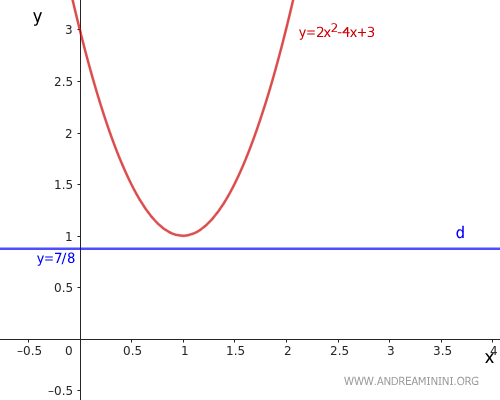
Now, we calculate the focus (F) of the parabola:

$$ F \begin{pmatrix} - \frac{b}{2a} \ , \ \frac{1 - Δ}{4a} \end{pmatrix} $$

Substituting a = 2, b = -4, c = 3, and the known discriminant Δ = -8, we get:

$$ F \begin{pmatrix} - \frac{-4}{2 \cdot 2} \ , \ \frac{1 - (-8)}{4 \cdot 2} \end{pmatrix} $$

$$ F \begin{pmatrix} - \frac{-4}{4} \ , \ \frac{9}{8} \end{pmatrix} $$

$$ F \begin{pmatrix} 1 \ , \ \frac{9}{8} \end{pmatrix} $$

Therefore, the focus F of the parabola is at the coordinates (x, y) = (1, 9/8).

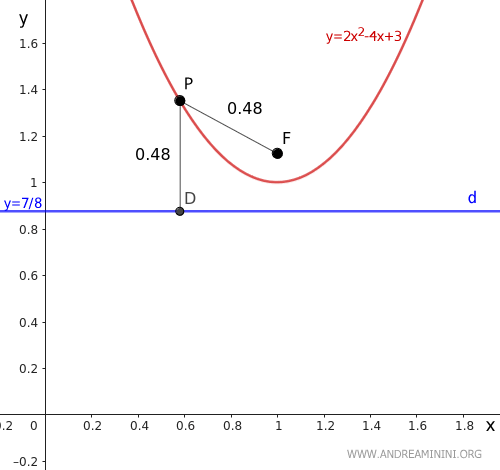
For a quick verification, we can take any point P and measure the distance to the focus F and the directrix d.

The distances are the same, PF ≈ PD, confirming the calculation is correct.

Next, we calculate the equation of the axis of the parabola:

$$ x = - \frac{b}{2a} $$

Knowing that a = 2 and b = -4, the calculation is straightforward:

$$ x = - \frac{-4}{2 \cdot 2} = - \frac{-4}{4} = 1 $$

Thus, the axis of the parabola is a vertical line, parallel to the y-axis, passing through x = 1.

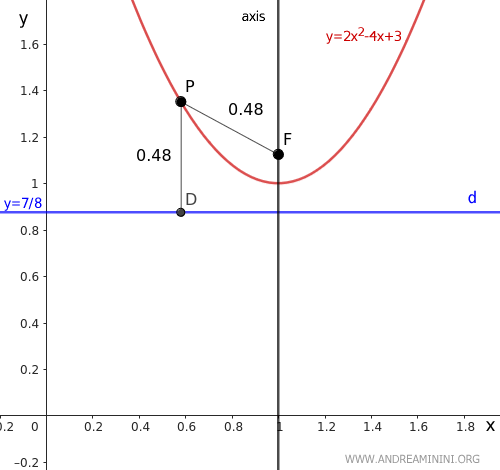
By definition, the axis is perpendicular to the directrix (d) and passes through the vertex (V) of the parabola.

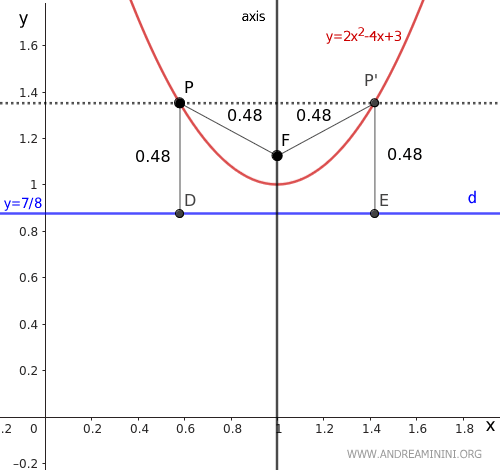
In the case of a parabola, the axis is also the axis of symmetry.

This means that for every point P, there is another point P' that is equidistant from the focus (F) and the directrix (d).

Finally, we calculate the coordinates of the vertex (V) of the parabola and check if it lies on the axis:

$$ V \begin{pmatrix} - \frac{b}{2a} \ , \ - \frac{Δ}{4a} \end{pmatrix} $$

Knowing that a = 2, b = -4, c = 3, and the discriminant is Δ = -8:

$$ V \begin{pmatrix} - \frac{-4}{2 \cdot 2} \ , \ - \frac{-8}{4 \cdot 2} \end{pmatrix} $$

$$ V \begin{pmatrix} - \frac{-4}{4} \ , \ - \frac{-8}{8} \end{pmatrix} $$

$$ V \begin{pmatrix} 1 \ , 1 \end{pmatrix} $$

The vertex V is at the coordinates (x, y) = (1, 1).

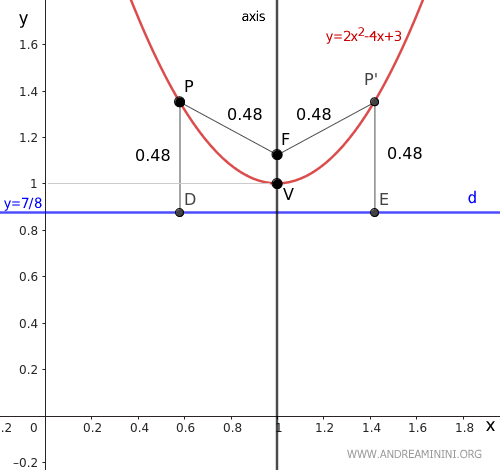
The vertex V of the parabola lies on the axis, confirming the calculation is correct.

The Graph of a Parabola

The graph of a parabola is the graph of a quadratic function of the form $$ y = ax^2 + bx + c $$ with a ≠ 0. It is an open, second-order plane algebraic curve, symmetric with respect to its own axis.

The equation of a parabola is:

$$ y = ax^2 + bx + c $$

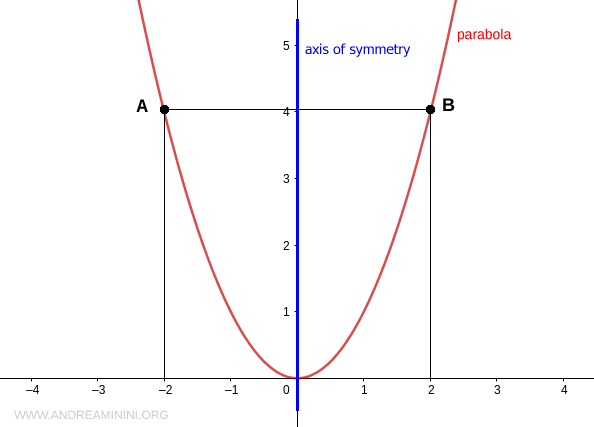
Graphically, every parabola is characterized by an axis of symmetry.

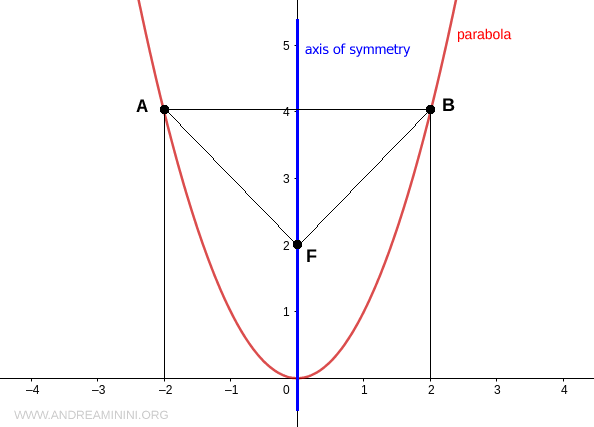
For any two points A and B on the parabola with the same ordinate, these are symmetric points and equidistant from the axis of symmetry.

They are also equidistant from any other fixed point on the axis of symmetry called the focus (F).

The point where the graph of the parabola intersects the axis of symmetry is called the vertex (V) of the parabola.

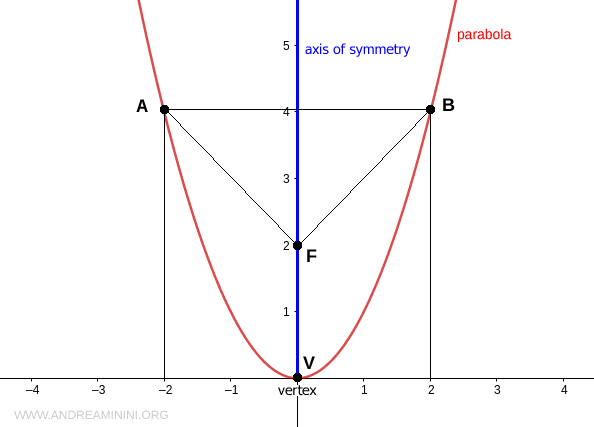
If the equation of the parabola is y = ax², the vertex of the parabola coincides with the origin O(0,0) of the Cartesian plane.

The sign of the coefficient a determines the concavity of the parabola.

• a > 0
  If a > 0, the parabola opens upwards.
• a < 0
  If a < 0, the parabola opens downwards.

The absolute value of the coefficient |a| determines the width of the parabola.

The greater the absolute value |a|, the narrower the parabola opens.

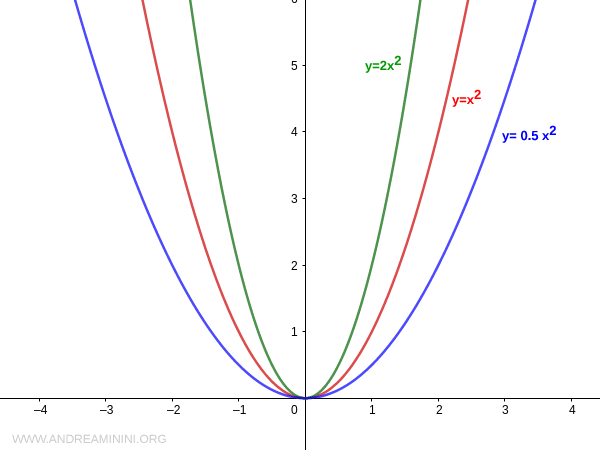
The same applies if the coefficient a is negative:

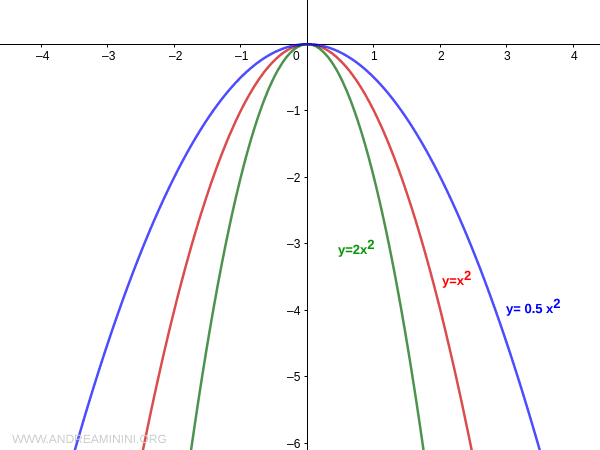
Note: The coefficient a of the parabola's equation must be non-zero because if it were zero, the function would graph as a constant function.

Observations

Some personal observations and notes on parabolas:

• The parabola is a conic section
  The parabola is one of the conic sections, along with the hyperbola, ellipse, and circle. For a parabola, the cone is cut by a plane parallel to the generating line of the cone, intersecting only one nappe. Thus, the parabola appears as an open and unbounded curve.
  

  

• The axis of the parabola is also the axis of symmetry
  This means that for every point on the parabola, there is another point on it that is symmetric to the first with respect to this axis.
• Parabola width and the absolute value of the coefficient "a"
  The width of the parabola is determined by the absolute value of the coefficient "a" in the equation y = ax² + bx + c. When |a| is large, the parabola becomes narrower. Conversely, when |a| is small, the parabola becomes wider.
  

  

• Concavity direction and the sign of the coefficient "a"
  The sign of the coefficient "a" in the equation y = ax² + bx + c determines the direction in which the parabola opens. If a > 0, the parabola opens upwards and is concave upwards. If a < 0, the parabola opens downwards and is concave downwards.
  

  

  Note: A curve is defined as concave if the segment connecting two points on the curve lies completely below the curve.

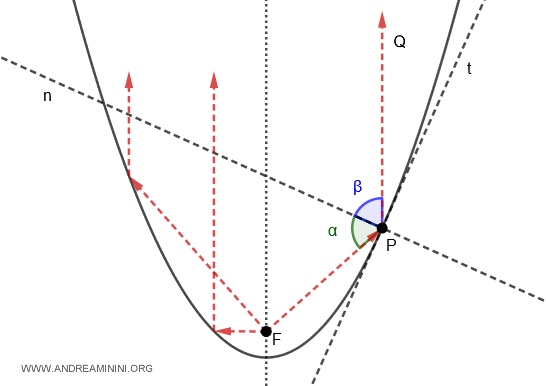
• Optical Property of the Parabola
  In a parabola, if you draw the tangent line (t) at a point P on the curve, the perpendicular line (n) to the tangent splits the angle formed by the focal ray $ PF $ and the ray $ PQ $ (which is parallel to the focal axis) into two equal angles, $ \alpha \cong \beta $.
  
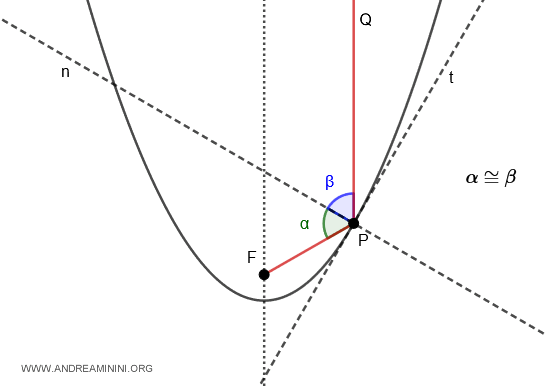
  This indicates that in a parabolic mirror, any ray parallel to the focal axis is reflected directly towards the focal point (F). As a result, all rays parallel to the focal axis converge at a single point. This principle is the basis for satellite dish antennas and concentrated solar power panels.
  
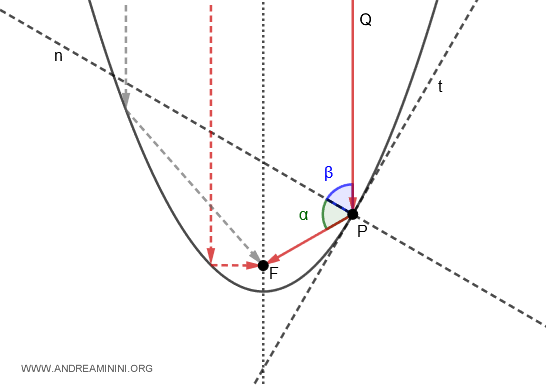
  Conversely, if the focal point (F) is a light source, all the rays reflected by the parabolic mirror will run parallel to the focal axis.
  

And so on.