Equation of a Rotated Parabola with an Oblique Axis

To describe a parabola with its vertex at \( (h, k) \) and an axis of symmetry inclined at an angle \(\alpha\), we need to recognize that a parabola with an inclined axis results from an isometric rotation.

For example, if we rotate the coordinates of a point (x,y) by an angle \(-\alpha\), we obtain new coordinates (x',y'):

$$ x' = (x - h) \cos(\alpha) + (y - k) \sin(\alpha) $$

$$ y' = -(x - h) \sin(\alpha) + (y - k) \cos(\alpha) $$

Thus, if the original equation of the parabola with its axis parallel to the y-axis is:

$$ y = ax^2 $$

The parabola in the new coordinates \( (x', y') \) has the standard equation:

$$ y' = a (x')^2 $$

Substituting \( x' \) and \( y' \) into the equation $ y' = a (x')^2 $, we obtain the rotated equation:

$$ -(x - h) \sin(\alpha) + (y - k) \cos(\alpha) = a \left[ (x - h) \cos(\alpha) + (y - k) \sin(\alpha) \right]^2 $$

If the original parabola is given in the canonical form with a vertical axis, \( (x - h)^2 = 4p(y - k) \), after rotation by \(\alpha\), the equation becomes:

$$ (x' - h)^2 = 4p(y' - k) $$

Substituting the rotated coordinates $ x' $ and $ y' $, we get:

$$ \left[(x - h) \cos(\alpha) + (y - k) \sin(\alpha)\right]^2 = 4p \left[-(x - h) \sin(\alpha) + (y - k) \cos(\alpha)\right] $$

These are the equations for the rotated parabola.

A Practical Example

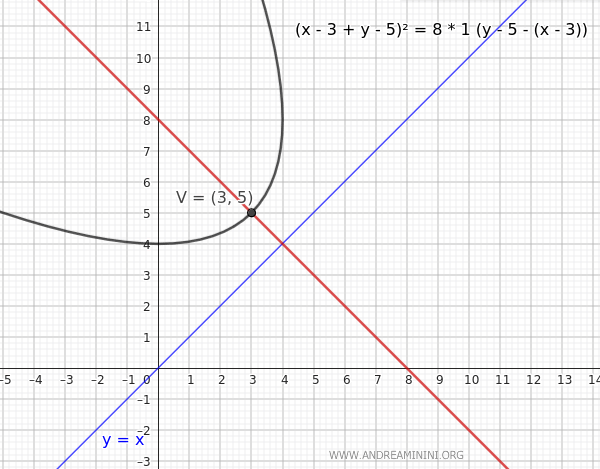
Consider a parabola with its vertex at $ V(h,k)=(3,5) $ and inclined at an angle of 45°, which means \(\alpha = 45^\circ\) or \(\alpha = \frac{\pi}{4}\):

The equation of the rotated parabola is:

$$ \left[(x - h) \cos(\alpha) + (y - k) \sin(\alpha)\right]^2 = 4p \left[-(x - h) \sin(\alpha) + (y - k) \cos(\alpha)\right] $$

Substituting $ h=3 $, $ k=5 $, and $ \alpha=45° $:

$$ \left[(x - 3) \cos(45°) + (y - 5) \sin(45°)\right]^2 = 4p \left[-(x - 3) \sin(45°) + (y - 5) \cos(45°)\right] $$

Knowing that $ \cos(45^\circ) = \sin(45^\circ) = \frac{1}{\sqrt{2}} $, the equation becomes:

$$ \left[(x - 3) \frac{1}{\sqrt{2}} + (y - 5) \frac{1}{\sqrt{2}}\right]^2 = 4p \left[-(x - 3) \frac{1}{\sqrt{2}} + (y - 5) \frac{1}{\sqrt{2}}\right] $$

Simplifying the terms, we get:

$$ \left[(x - 3) + (y - 5)\right]^2 = 8p \left[(y - 5) - (x - 3)\right] $$

Expanding and simplifying further, we derive the correct equation for the rotated parabola.

And so on.