Tangent Lines to a Parabola

Given a parabola and any point P on the plane, there can be two, one, or no tangent lines to the parabola passing through point P.

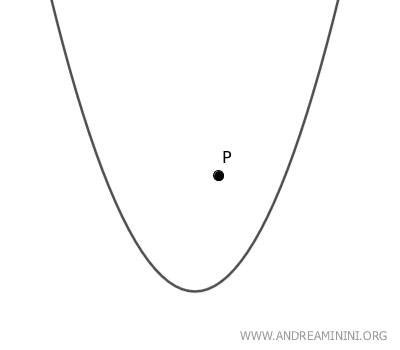
• If point P is outside the parabola, there are two tangent lines to the parabola passing through P.
  
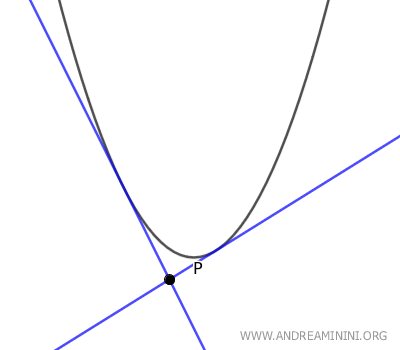
• If point P is on the parabola, there is exactly one tangent line to the parabola passing through P.
  
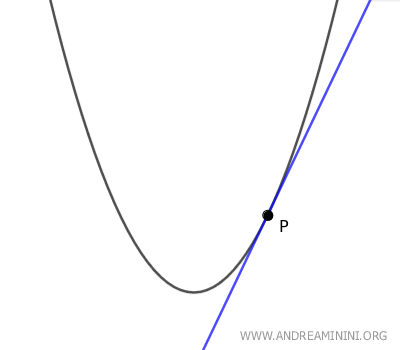
• If point P is inside the parabola, there are no tangent lines to the parabola passing through P.
  

How to Find Tangent Lines to a Parabola

To determine the number and nature of tangent lines to a parabola passing through a point P, start with the equation of the family of lines passing through point \( P(x_0, y_0) \):

$$ y - y_0 = m (x - x_0) $$

We need to find which of these lines intersect the parabola given by:

$$ y = ax^2 + bx + c $$

Thus, we create a system of equations using the line equation and the parabola equation:

$$ \begin{cases} y - y_0 = m (x - x_0) \\ y = ax^2 + bx + c \end{cases} $$

The solutions to this system represent the intersection points between the lines and the parabola, including tangent and secant lines. 

To isolate the tangent lines, we need to apply the tangency condition.

A line is tangent to a curve if the resulting quadratic equation from the intersection has a single solution, meaning two coincident solutions, which occurs when the discriminant is zero:

$$ \Delta = b^2 - 4ac = 0 $$

This condition allows us to determine the slope \( m \) of the tangent lines to the parabola.

Once we find the slope \( m \), we substitute it back into the line equation to identify the tangent lines.

A Practical Example

Consider the parabola with the equation:

$$ y=x^2+2x+3 $$

We need to find the tangent lines to the parabola passing through point P(-1,1).

The equation of the family of lines passing through point P is:

$$ (y-y_0) = m(x-x_0) $$

Here, the coordinates of point P(-1,1) are x0=-1 and y0=1

$$ (y-1) = m(x-(-1)) $$

$$ (y-1) = m(x+1) $$

We find the lines from the family that intersect with the parabola:

$$ \begin{cases} y=x^2+2x+3 \\ (y-1) = m(x+1) \end{cases} $$

$$ \begin{cases} y=x^2+2x+3 \\ y = m(x+1) +1 \end{cases} $$

The resulting quadratic equation is:

$$ x^2+2x+3 = m(x+1)+1 $$

$$ x^2+2x+3 = mx+ m +1 $$

$$ x^2+2x+3 - mx- m -1 $$

$$ x^2+2x- mx- m +2 $$

$$ x^2+x(2-m) +2- m $$

The discriminant of this quadratic equation is:

$$ \Delta = b^2-4ac $$

Here, the coefficients are a=1, b=(2-m), and c=2-m

$$ \Delta = (2-m)^2-4 \cdot 1 \cdot (2-m) $$

$$ \Delta = 4-4m+m^2-8+4m $$

$$ \Delta = m^2-4 $$

Now we impose the tangency condition \( \Delta = 0 \):

$$ \Delta = m^2-4 = 0 $$

To find the slopes (m) of the tangent lines, we solve the quadratic equation:

$$ m^2-4 = 0 $$

We calculate the solutions of the resulting equation:

$$ m = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$

The coefficients of the equation \( m^2-4 = 0 \) are a=1, b=0, and c=-4

$$ m = \frac{0 \pm \sqrt{16}}{2} $$

$$ m = \frac{0 \pm 4}{2} $$

$$ m = \begin{cases} \frac{0 - 4}{2} = -2 \\ \frac{0 + 4}{2} = 2 \end{cases} $$

The system has two solutions, so there are two tangent lines to the parabola.

The slopes of the tangent lines are m=-2 and m=2

We substitute them back into the line equation to obtain the equations of the tangent lines:

• If m=-2 $$ (y-1) = m(x+1) $$ $$ (y-1) = -2(x+1) $$ $$ y = -2x-2+1 $$ $$ y = -2x-1 $$
• If m=2 $$ (y-1) = m(x+1) $$ $$ (y-1) = 2(x+1) $$ $$ y = 2x+2+1 $$ $$ y = 2x+3 $$

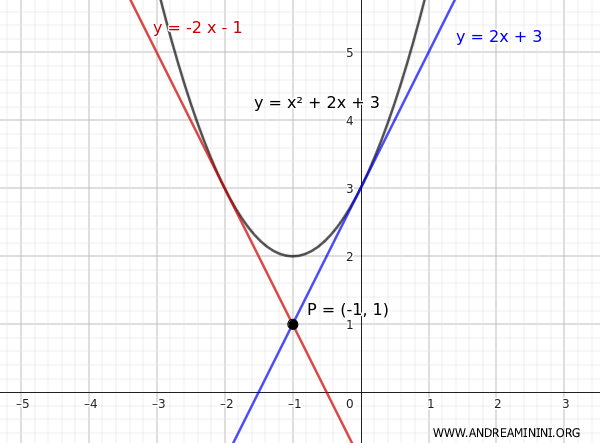
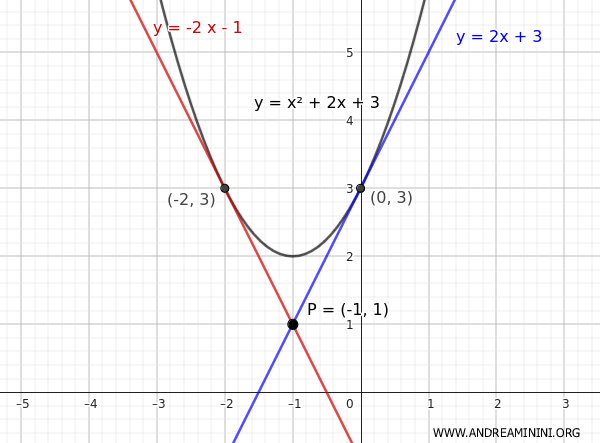
Therefore, the tangent lines to the parabola passing through point P(-1;1) are:

• $ y = -2x-1 $
• $ y = 2x+3 $

Here is the graphical representation of the solution:

To find the coordinates of the points of tangency, we solve the systems of equations composed of the line and parabola equations. In this case, the first system is:

$$ \begin{cases} y=x^2+2x+3 \\ y = -2x-1 \end{cases} $$

$$ \begin{cases} -2x-1 = x^2+2x+3 \\ y = -2x-1 \end{cases} $$

$$ \begin{cases} x^2+4x+4=0 \\ y = -2x-1 \end{cases} $$

The equation \( x^2+4x+4=0 \) has a single solution \( x = -2 \) because \( \Delta = 0 \)

$$ \begin{cases} x=-2 \\ y = -2x-1 \end{cases} $$

$$ \begin{cases} x=-2 \\ y = -2 \cdot (-2) -1 \end{cases} $$

$$ \begin{cases} x=-2 \\ y = 3 \end{cases} $$

Thus, one point of tangency is at coordinates (-2,3)

The second system is:

$$ \begin{cases} y=x^2+2x+3 \\ y = 2x+3 \end{cases} $$

$$ \begin{cases} 2x+3 = x^2+2x+3 \\ y = 2x+3 \end{cases} $$

$$ \begin{cases} x^2=0 \\ y = 2x+3 \end{cases} $$

$$ \begin{cases} x=0 \\ y = 2 \cdot 0 + 3 \end{cases} $$

$$ \begin{cases} x=0 \\ y = 3 \end{cases} $$

The other point of tangency is at coordinates (0,3)

And so on.