Paraboloid

A paraboloid is a type of quadric surface in three-dimensional space that originates from a parabola.

There are two main types of paraboloids, depending on how they’re generated: either by rotating or translating a parabola.

• Elliptical Paraboloid
  This surface is created by rotating a parabola around its axis of symmetry, typically the vertical axis. The result is a shape that resembles a cup or a deep dish. Horizontal cross-sections of this surface are ellipses, while vertical cross-sections are parabolas. The general equation for an elliptical paraboloid is: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = \frac{z}{c} $$ where \(a\) and \(b\) are the semi-axes of the ellipse formed in the horizontal sections, and \(c\) is a parameter that controls the opening of the paraboloid.
  
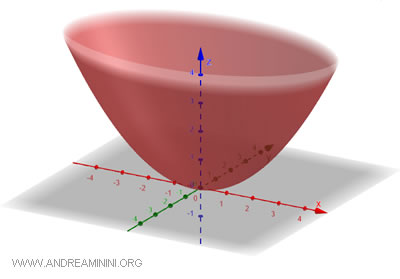
  It’s called "elliptical" because when a plane intersects the paraboloid horizontally, the resulting cross-section is an ellipse.
  
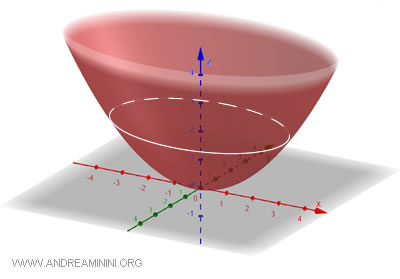
  Specifically, if \(a = b\), the equation simplifies to that of a "paraboloid of revolution": $$ x^2 + y^2 = 2pz $$ where \(p\) is a parameter related to the paraboloid’s opening.
  
  

  A common example is a satellite dish, which uses the elliptical shape to collect and focus signals transmitted from space. The paraboloid of revolution is particularly effective because it can reflect parallel rays toward a single focal point, concentrating a large amount of information in one place. This optical property is invaluable in the design of antennas and telescopes.

• Hyperbolic Paraboloid
  This surface is formed by translating a parabola along a direction that is not parallel to its axis of symmetry. The result is a shape where horizontal sections are hyperbolic, while vertical sections remain parabolic. The general equation for a hyperbolic paraboloid is: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \frac{z}{c} $$ where \(a\) and \(b\) are parameters that determine the extent of the hyperbola in the horizontal sections, and \(c\) controls the paraboloid’s opening.
  
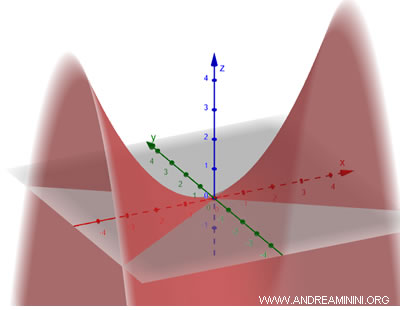
  It’s called "hyperbolic" because when a plane intersects the paraboloid horizontally, the resulting cross-section is a hyperbola.
  

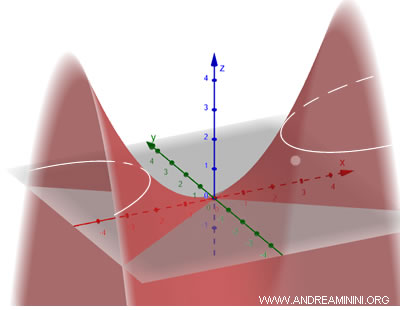
  A practical application of hyperbolic paraboloids is in architecture, where they are used to create curved roofs that efficiently distribute the weight of the structure.

In both cases, the vertical cross-sections are parabolas, which is why these surfaces are referred to as "paraboloids."

In summary, while both types of paraboloids are derived from parabolas, they differ in shape and application.

And so on.