Equidecomposable Solids

Two solids are said to be equidecomposable (or equicomposable) if they can each be divided into a finite number of solid parts such that every piece from one solid is congruent to a corresponding piece from the other. Crucially, these parts must be three-dimensional solids - not merely surfaces or lines.

In plain terms: two solids are equidecomposable if you can “disassemble” one into pieces that exactly match those of the other, with no gaps, overlaps, or distortions.

Each part of the first solid must match the corresponding part of the second in both shape and size.

No stretching or compressing is allowed - this is a purely geometric reconstruction.

Equidecomposable solids must necessarily have the same volume, since their corresponding parts occupy identical spatial regions.

Note. The converse does not always hold: two solids may have the same volume but not be equidecomposable.

Practical Example

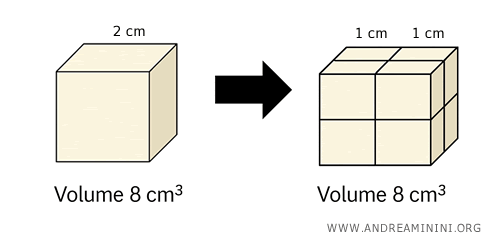
Consider a cube with sides of 2 cm. Its volume is 8 cm³.

Now imagine breaking it down into eight smaller cubes, each with 1 cm sides, and rearranging them into a new cube with the same volume.

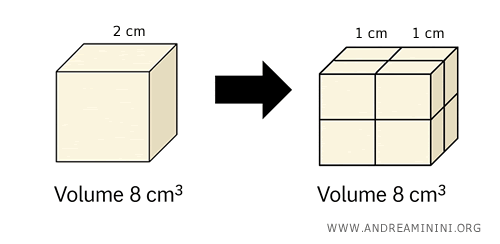
By assembling these eight unit cubes into a new cube, we obtain a solid that is equidecomposable with the original.

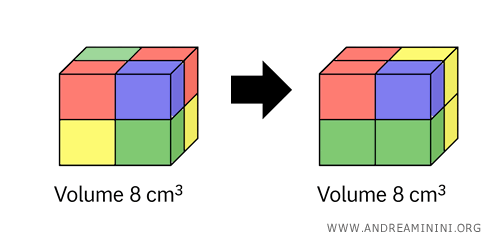
In this case, the two solids are equidecomposable because they are built from the same set of congruent unit cubes.

They are also equivalent in volume, since they both occupy 8 cm³ of space.

Example 2

Let’s look at two rectangular prisms with square bases:

The first has a base of 2 cm by 2 cm and a height of 3 cm.

The second has a base of 1 cm by 1 cm and a height of 12 cm.

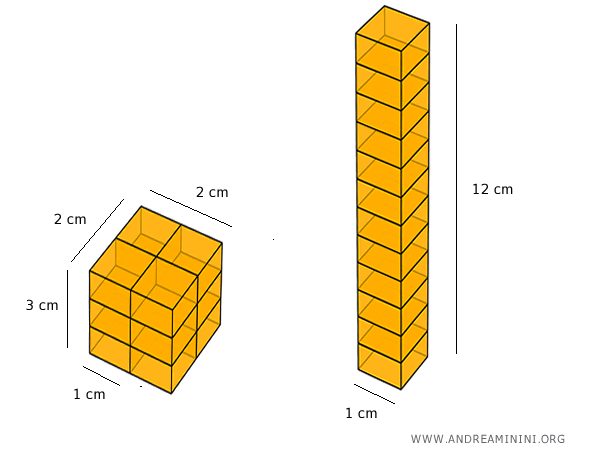
Both have a volume of 12 cm³ and are equidecomposable because each can be partitioned into congruent rectangular blocks using straightforward cuts.

Example 3

Now consider a square-based pyramid with a base of 1 cm per side and a height of 3 cm, alongside a cube with sides of 1 cm.

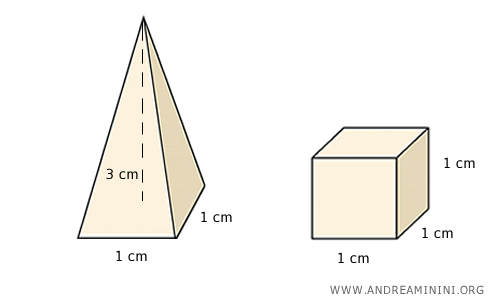
The volume of the pyramid is:

$$ V_p = \frac{1}{3} l^2 \cdot h = \frac{1}{3} \cdot (1 \ cm)^2 \cdot 3 \ cm = 1 \ cm^3 $$

The cube also has a volume of 1 cm³.

However, despite having equal volumes, a regular square-based pyramid and a cube are not equidecomposable.

There is no way to decompose a pyramid into a finite number of solid parts that are congruent to those of a cube - at least not within the framework of elementary geometry. Doing so would require advanced and abstract mathematical constructions.

This illustrates that equal volume alone is not sufficient for equidecomposability.

Difference Between Equivalent and Equidecomposable Solids

In geometry, equidecomposability is a stricter condition than equivalence.

• Equivalent solids have the same volume, but might not share any deeper geometric relationship.
• Equidecomposable solids are also equivalent in volume, but satisfy a stronger geometric constraint: they can be broken down and reassembled using congruent solid parts.

Equidecomposability is a powerful concept in geometry - it goes beyond volume, encouraging us to view space as something that can be broken apart and rebuilt, like a three-dimensional puzzle.

Note. In classical solid geometry, proving that two solids are equidecomposable is far from trivial. It depends on the internal geometric structure, not just external measurements.

Equidecomposability Theorem

If two solids are equidecomposable, then they are also equivalent - that is, they occupy the same volume.

In other words, equidecomposability guarantees volume equivalence between solids.

The converse, however, does not hold: two solids can share the same volume (i.e., be equivalent) without being equidecomposable - as is the case with a sphere and a cube.

So, equidecomposability is a stronger condition: it’s not enough for two solids to have the same volume - they must also be decomposable into a finite number of congruent parts that can be reassembled to form each other.

Note. Imagine building a wall out of toy bricks. Then you dismantle it and use the exact same bricks to build a tower. Although the shapes are different, both structures are composed of the same elements. In solid geometry, we say the two constructions are equidecomposable. Since each brick has the same volume, the tower must have the same volume as the wall. Therefore, the two solids are also volume-equivalent.

The concept was first introduced - albeit in a non-modern form - by Euclid in The Elements, Book XII.

It was later refined during the Renaissance and rigorously formalized by Bonaventura Cavalieri, who explored the idea of equal cross-sectional areas. His work culminated in what is now known as Cavalieri’s Principle.

Concrete Example

Consider two solids, $\mathbb{U}$ and $\mathbb{V}$, illustrated in the diagram below (not included here).

Solid $\mathbb{U}$ consists of three parts: $\mathbb{U}_1$, $\mathbb{U}_2$, and $\mathbb{U}_3$.

Likewise, solid $\mathbb{V}$ is composed of three parts: $\mathbb{V}_1$, $\mathbb{V}_2$, and $\mathbb{V}_3$.

Suppose the following congruences hold:

$\mathbb{U}_1 \cong \mathbb{V}_1$,

$\mathbb{U}_2 \cong \mathbb{V}_2$,

$\mathbb{U}_3 \cong \mathbb{V}_3$.

Since each component of $\mathbb{U}$ is congruent to its counterpart in $\mathbb{V}$, it follows that the two solids are equidecomposable.

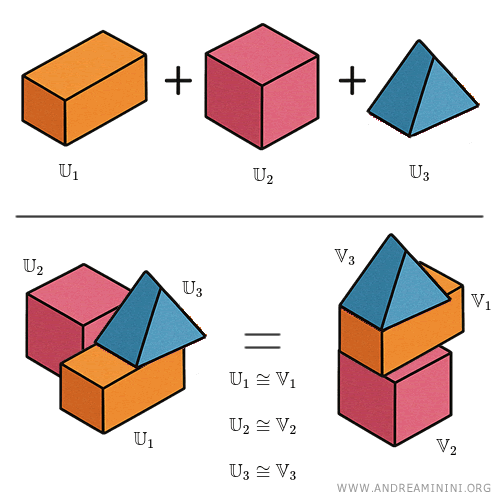
According to the theorem, these solids must also be equivalent, as they occupy the same volume in space - even though their overall shapes may differ.

The Dehn Invariant

In three-dimensional geometry, equal volume doesn’t guarantee equidecomposability.

The key obstruction is a mathematical quantity known as the Dehn invariant, introduced in 1900 by German mathematician Max Dehn. It represents the fundamental barrier to equidecomposing certain solids.

The Dehn invariant captures information about the dihedral angles - the angles formed between the faces of a solid - and how these angles combine across the shape.

If two polyhedra have different Dehn invariants, then they are not equidecomposable.

This result proves, for instance, that there is no way to cut a cube into a finite number of congruent solids and reassemble them into a tetrahedron of the same volume - because their Dehn invariants differ.

In summary:

• In two dimensions, any two polygons with the same area are equidecomposable (Bolyai - Gerwien Theorem).
• In three dimensions, the Dehn invariant comes into play - and puts strict limits on what’s possible.

This marks the boundary of equidecomposability - or at least one of its first frontiers. Beyond it lie deeper challenges, involving measure theory, non-measurable decompositions, and broader notions of congruence in more abstract spaces.

Notes

Some additional remarks and insights on equidecomposability:

• The Banach - Tarski Paradox
  The Banach - Tarski paradox asserts that, under certain theoretical conditions (notably assuming the Axiom of Choice), a solid sphere can be partitioned into a finite number of subsets that can be rearranged - using only rotations and translations - into two identical copies of the original sphere. It seems paradoxical, and indeed it is.

  Note. This paradox does not violate classical geometry - it bypasses it entirely. The “pieces” involved are not physical solids, nor are they geometrically describable: they are non-measurable sets, with no well-defined volume, constructed using purely abstract logic. For this reason, Banach - Tarski is not a valid example of equidecomposability. It doesn’t involve congruent pieces, it doesn’t preserve measure, and it operates completely outside the realm of classical dissection theory. It illustrates the bizarre consequences of pushing set theory beyond intuitive limits.

And so on.