Ellipsoid

An ellipsoid is a three-dimensional geometric shape that can be visualized as a stretched or flattened version of a sphere.

In other words, it's a smooth, closed surface similar to a sphere but with different proportions along its x, y, and z axes.

An ellipsoid is created by rotating an ellipse around one of its axes of symmetry.

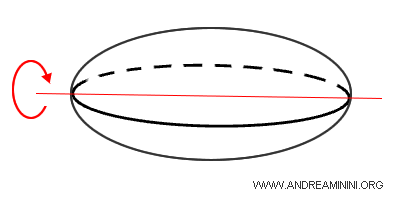
ellipse rotation

An ellipse is a shape that resembles a circle but has two axes of different lengths: one longer and one shorter.

When you rotate an ellipse, it generates a shape with three dimensions: height, width, and depth.

The Ellipsoid Equation
A Practical Example
Types of Ellipsoids

The Ellipsoid Equation

Mathematically, the equation of an ellipsoid is:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 $$

Here, $x$, $y$, and $z$ represent the coordinates of the points on the surface of the ellipsoid in space.

The letters $a$, $b$, and $c$ stand for the lengths of the three semi-axes, which define the shape of the ellipsoid.

These semi-axes are like the radii of a sphere, but instead of being equal, they can have different lengths. The equation is as follows:

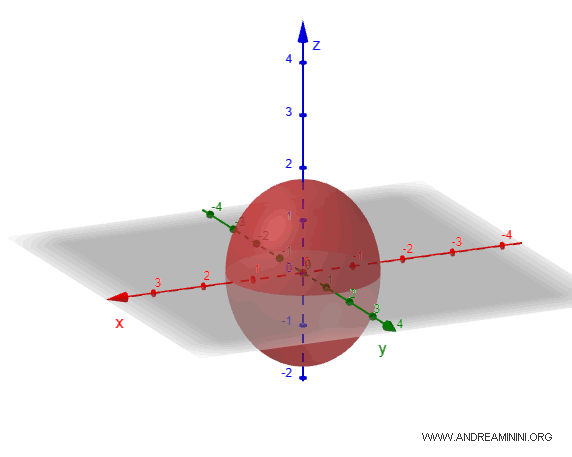
A Practical Example

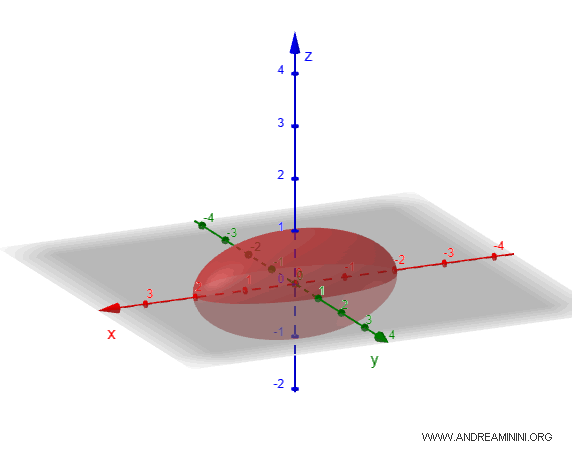
Let's consider an ellipsoid where the semi-axes are $a=2$, $b=1$, and $c=1$.

The equation of this ellipsoid is:

$$ \frac{x^2}{2^2} + \frac{y^2}{1} + \frac{z^2}{1} = 1 $$

$$ \frac{x^2}{4} + y^2 + z^2 = 1 $$

When we plot this solid, the ellipsoid appears as an elongated and flattened sphere.

ellipsoid example

Types of Ellipsoids

There are different types of ellipsoids, depending on how their semi-axes are arranged:

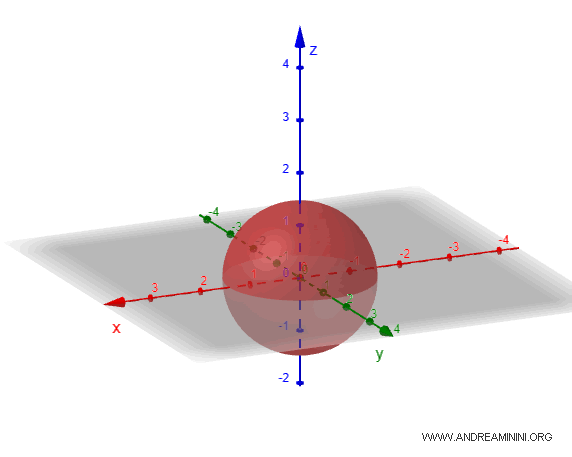
Spherical Ellipsoid
If all three semi-axes $a$, $b$, and $c$ are equal, the ellipsoid becomes a perfect sphere. In this case, the shape is symmetrical in all directions, and any plane passing through the center creates a perfect circle.
Oblate Ellipsoid
This type of ellipsoid occurs when two of the semi-axes, say $a$ and $b$, are equal, while the third, $c$, is shorter. This results in a shape that's flattened at the poles, similar to a squashed disk. A real-world example of an oblate ellipsoid is the Earth, which is slightly flattened at the poles due to its rotation.
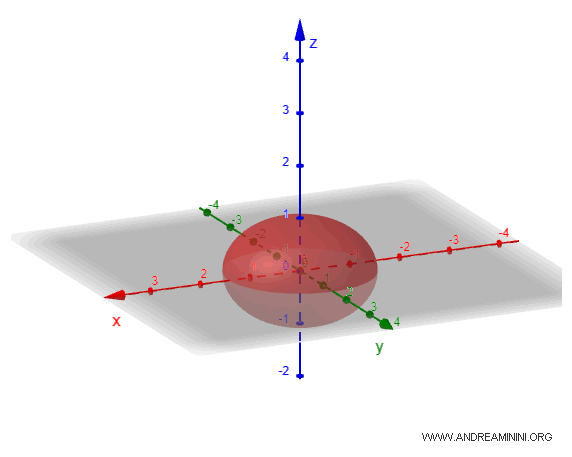
Prolate Ellipsoid
In this case, two semi-axes, $a$ and $b$, are equal, but the third, $c$, is longer. This type of ellipsoid is elongated along one axis, resembling a rugby ball. It's like a sphere stretched along a specific direction.

Note. Ellipsoids aren’t just abstract concepts; they have practical applications in many fields. In astronomy, ellipsoids help describe the shape of celestial bodies like planets or stars that aren’t perfectly spherical due to their rotation. For instance, an oblate ellipsoid is used to represent the actual shape of the Earth.

In summary, an ellipsoid is a geometric shape that extends the concept of a sphere, adapting to various natural and artificial forms found in the world and the universe.