Cavalieri's Principle

Two solids have equal volume if, for every plane parallel to a given direction (typically horizontal), the area of the cross-section formed by intersecting the first solid is the same as that of the second.

This principle is particularly useful when dealing with solids whose volumes are difficult to compute using standard formulas.

If I can prove that each cross-section of one solid matches the corresponding cross-section of another in area, then I can conclude the two are volume-equivalent solids, even if their overall shapes are quite different.

The solids don’t need to be identical or symmetrical in any way.

Example. Imagine two stacks of perfectly rectangular sheets, identical in number and dimensions. If every sheet is the same, the stacks are congruent - same volume, same shape, same height. But if I shift the sheets sideways in one of the stacks, creating a slanted shape (like a leaning pile), intuition suggests the volume remains unchanged. Same number of layers, same height - so the same amount of space is occupied.

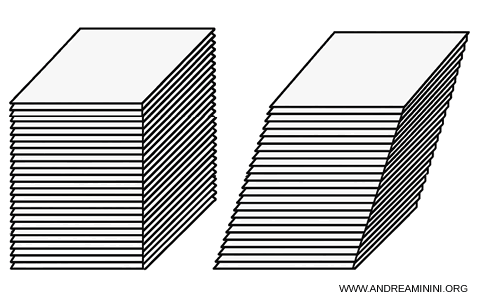
This elegantly simple yet revolutionary idea was introduced by Bonaventura Cavalieri in the 17th century. It has since become known as Cavalieri’s Principle.

A Limitation of Cavalieri’s Principle

Cavalieri’s Principle provides a sufficient but not necessary condition for volume equivalence.

If the cross-sections are equal at every height, then the volumes must be equal.

However, the converse doesn’t always hold: two solids can have the same volume without satisfying the conditions of Cavalieri’s Principle.

Example. Two solids might enclose the same volume yet have different cross-sections at corresponding heights. That is, even though they occupy the same amount of space, there’s no way to align them such that every horizontal slice matches. For instance, the two solids below share the same volume, but they fail to meet the requirements of Cavalieri’s Principle.

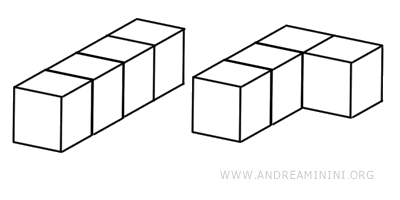
This highlights a key limitation: the principle does not fully characterize volume equivalence. Instead, it offers a valuable but partial criterion.

In essence, it’s a partial method that was once treated as comprehensive. Cavalieri’s approach overlooks the full spatial complexity of solids, reducing three-dimensional objects to a sequence of two-dimensional slices.

It's a bit like claiming two novels are the same just because a randomly chosen sentence from each has the same number of words.

Note. Still, in Cavalieri’s historical context, the idea was nothing short of brilliant - mainly because there was no analytical framework at the time for rigorously treating volume. In the barren mathematical landscape of the 17th century, Cavalieri’s Principle felt like a breakthrough. Its limitations only became evident later, with the development of more robust tools like integral calculus and topology.

Additional Remarks

Some side notes and personal reflections on Cavalieri’s Principle:

• Integral Calculus
  Cavalieri’s Principle can be seen as a geometric precursor to integration: comparing slices mirrors the process of summing infinitesimal areas, just as we do in definite integrals. His “Geometry of Indivisibles” anticipates the idea of continuous summation on which integral calculus is built.
• The Two-Dimensional Version
  Two planar figures have the same area if, for every line in a fixed direction, the lengths of the segments formed by intersecting the two figures are equal.

And so on.