Equivalent Solids

Two solids are considered equivalent when they have the same volume, even if their shapes are completely different. \[ V_A = V_B \] Here, \( V_A \) and \( V_B \) represent the volumes of the two solids.

This concept concerns only the amount of space a solid occupies - it has nothing to do with its shape or surface area.

Objects can look entirely different yet occupy the same volume.

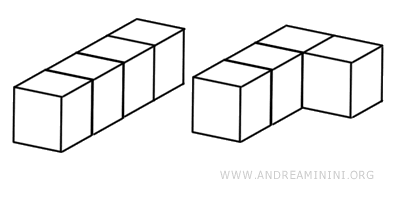
So, equivalence doesn’t imply that solids share the same height, base, or surface area - only that they contain the same amount of space (volume).

A Practical Example

A cube with edges measuring 3 cm has a volume of 27 cm³:

\[ V = 3^3 = 27 \ cm^3 \]

A rectangular prism with a base of 3 cm × 3 cm and a height of 3 cm also has a volume of 27 cm³:

\[ V = 3^3 = 27 \ cm^3 \]

Likewise, a cylinder with a base area of 9 cm² and a height of 3 cm has the same volume:

\[ V = 9 \cdot 3 = 27 \ cm^3 \]

These are clearly different shapes, yet they are volumetrically equivalent.

Transformations That Preserve Volume

Many solids can be transformed into other shapes without altering their volume.

These transformations involve repositioning, cutting, and reassembling parts of the solid.

Example

A triangular prism can be divided into three pyramids of equal volume. By rearranging these pyramids, one can form a solid that is volumetrically equivalent to the original prism.

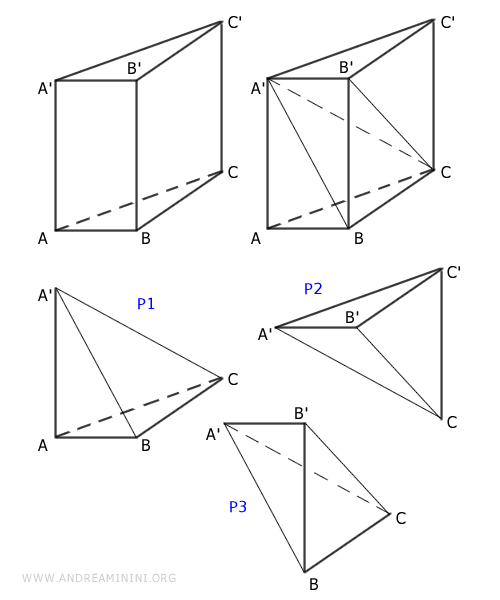
Note. Pyramids P1 and P2 share a congruent base $ ABC = A'B'C' $ and congruent height $ AA' = CC' $, making them equivalent. Pyramids P2 and P3 have congruent bases $ BCC' = BCB' $ and a common height $ A'B' $, so they too are equivalent. By the transitive property, P1 and P3 must also be equivalent.

The volume of a pyramid is given by the formula:

\[ V = \frac{1}{3} \cdot \text{base} \cdot \text{height} \]

While the volume of a prism is calculated as:

\[ V = \text{base} \cdot \text{height} \]

This shows that, when base and height are consistent, a pyramid has one-third the volume of a prism.

Therefore, combining three identical pyramids yields a prism of equal volume - proving that the two solids are equivalent.

Equivalence vs. Congruence

It's important to distinguish between equivalence and congruence.

• Congruence: solids have the same shape and size. For example, two identical cubes are congruent, and therefore also equivalent.
  
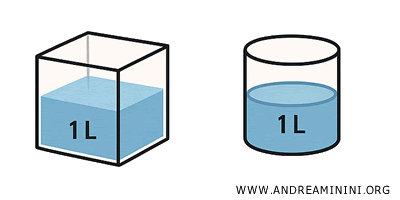
• Equivalence: solids share the same volume, regardless of shape. For example, a cube and a cylinder with equal volumes are equivalent, but not congruent.
  

In other words, "congruent" means identical in every respect - shape, size, and volume - whereas "equivalent" refers solely to having the same volume, even if the shapes differ.

So, when two solids are said to be "equivalent," it doesn’t imply that they are indistinguishable or that they can be perfectly aligned; it simply means they occupy the same amount of space.

Notes

Additional insights and personal reflections on the concept of solid equivalence.

• The sum or difference of congruent or equivalent solids yields solids of equal volume
  When a solid is formed by adding to or subtracting from other solids that are congruent (identical in both shape and size) or equivalent (identical in volume), the resulting solids will also share the same volume - meaning they are equivalent in a volumetric sense.
  

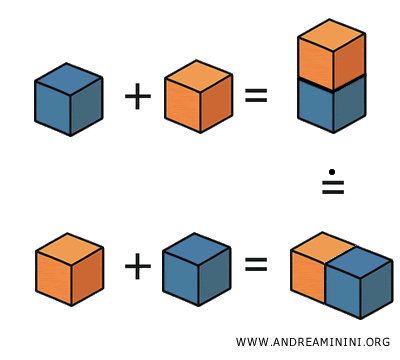
  Example. Suppose I have two identical cubes and remove the same pyramid from each. The remaining solids will be equivalent. If I then attach the same cylinder to both, the resulting shapes will still have equal volume, and thus remain equivalent.

• Exclusion Principle
  According to this postulate - commonly referred to as the exclusion principle - given any two solids A and B, one of the following three scenarios must hold:
  • A and B are equivalent: $ A \doteq B $, meaning they have the same volume.
  • A dominates B: $ A>B $. In this case, A has a greater volume than B.
  • A is subordinate to B: $ A<B $. In this case, A has a smaller volume than B.
  These cases are mutually exclusive.

  Note. This tripartite classification - equivalent, dominant, subordinate - rests on the assumption that any pair of solids can always be unambiguously compared. However, it neglects a rather common complication: two objects may not be comparable by a single criterion, especially when multiple or incommensurable attributes are involved, such as volume, symmetry, computational complexity, aesthetic value, and so on. The presence of multiple criteria does not, in itself, guarantee the possibility of establishing a consistent order. In fact, comparisons often break down entirely. Forcing every relationship into a total ordering risks flattening the inherent complexity of the real world. For instance, a marble cube and a wooden cube may share the same volume but differ radically in weight, density, cost, durability, or intended use - making them incomparable in any meaningful sense. Likewise, a sphere and a cube of equal volume diverge in terms of surface area, aerodynamics, and stability - that is, in all the properties that matter beyond mere measurement. Attempting to reduce such multifaceted differences to a single evaluative dimension amounts to an arbitrary oversimplification.

• De Zolt’s Postulate
  De Zolt’s postulate states that a solid cannot be equivalent to any of its proper parts - that is, it cannot share the same volume with a portion wholly contained within itself.
• Cavalieri’s Principle
  If the cross-sectional areas of two solids are equal at every height along a given direction, then the solids must have the same volume.

And so on.