Polyhedra
A polyhedron is a three-dimensional solid shape defined by flat faces, edges, and vertices.

The faces of a polyhedron are polygons (e.g., triangles, squares, pentagons, etc.) that lie on different planes, none of which intersect the solid. A polyhedron has at least four faces, with the simplest example being a tetrahedron. A pentahedron has five faces, a hexahedron has six, an octahedron has eight, and so on.
Edges are the line segments where two faces of a polyhedron intersect. They form the sides of the polygons that make up each face.
Each edge corresponds to a dihedral angle, which is the angle formed by the two adjoining faces that meet along that edge.
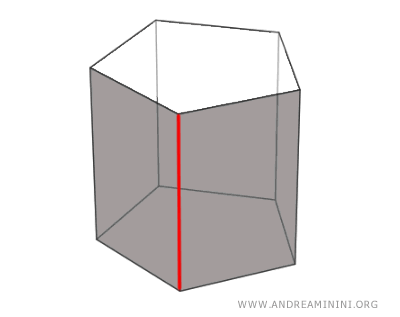
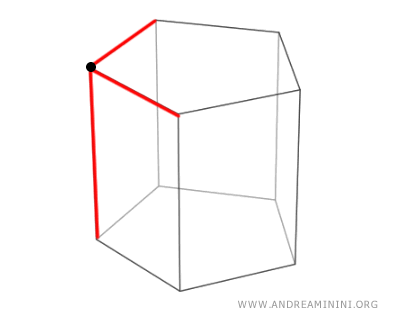
Vertices are the points where three or more edges converge. They are the corners of the polyhedron’s faces.
Each vertex is associated with a solid angle, defined by the edges and faces that meet at that point.
Polyhedra have fascinated mathematicians, artists, and philosophers for millennia. For example, Plato was particularly interested in regular polyhedra, now known as "Platonic solids." Beyond mathematics, polyhedra have various applications in science and engineering. For instance, many molecular structures in chemistry have polyhedral shapes. They are also widely used in architecture and art.
In a polyhedron, a diagonal is a line segment that connects two vertices that do not share the same face.
The surface area of a polyhedron is the total area of all its faces combined.
Regular and Irregular Polyhedra
Polyhedra are categorized as either regular or irregular.
- Regular Polyhedra (or Platonic Solids)
Regular polyhedra have identical faces and equal angles. Their faces are regular polygons, all congruent. The angles and dihedral angles are also congruent. Regular polyhedra are also known as Platonic solids.Note: In a plane, regular polygons can have any number of sides. However, in three-dimensional space, only five regular polyhedra exist: the tetrahedron, hexahedron, octahedron, dodecahedron, and icosahedron.
- Irregular Polyhedra
Irregular polyhedra do not have identical faces or angles. For example, a prism is a typical example of an irregular polyhedron because it can have bases of various polygonal shapes.
Euler's Formula
Euler's formula describes the relationship between the number of vertices (V), edges (E), and faces (F) of a simple and connected polyhedron (without holes).
For a simple and connected polyhedron, the number of vertices (V) minus the number of edges (E) plus the number of faces (F) always equals 2. $$ V - E + F = 2 $$
For example, a cube has 6 square faces, 8 vertices, and 12 edges.
$$ F = 6 $$
$$ V = 8 $$
$$ E = 12 $$
Substituting these values into Euler's formula:
$$ V - E + F = 2 $$
$$ 8 - 12 + 6 = 2 $$
$$ 2 = 2 $$
The equation is satisfied.
What is it used for? Euler's formula can be used to determine if a combination of vertices, edges, and faces can form a simple and connected polyhedron. If it doesn't satisfy Euler's formula, the combination cannot represent such a polyhedron. For example, this formula has been used to prove that there are exactly five regular polyhedra (the Platonic solids).
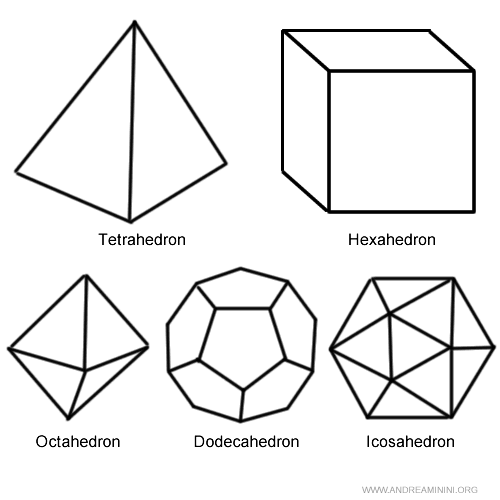
Platonic Solids
Platonic solids are the five known regular polyhedra.
- Tetrahedron
This polyhedron has 4 triangular faces, 4 vertices, and 6 edges. Each face is an equilateral triangle. - Hexahedron
This regular polyhedron is more commonly known as the "cube." It has 6 square faces, 8 vertices, and 12 edges. Each face is a square. - Octahedron
It has 8 triangular faces, 6 vertices, and 12 edges. - Dodecahedron
This polyhedron has 12 pentagonal faces, 20 vertices, and 30 edges. Each face is a pentagon. - Icosahedron
It has 20 triangular faces, 12 vertices, and 30 edges.
Proof
It can be rigorously demonstrated that there are exactly five regular polyhedra. This result stems from the fact that, at each vertex of a polyhedron, the sum of the interior angles of the faces meeting there must be strictly less than a full angle (360°).
Let’s begin with a regular polyhedron whose faces are congruent equilateral triangles.
Each angle in an equilateral triangle measures 60°. Therefore, no more than 5 such faces can meet at a vertex - since the total must remain below 360°. For example, $6 \times 60° = 360°$, which is already too much to allow a three-dimensional shape to form at that point.
| Regular polygon | Number of faces meeting at a vertex | Sum of face angles | Polyhedron |
|---|---|---|---|
| equilateral triangles (angles of 60°) |
3 | 180° < 360° | tetrahedron |
| 4 | 240° < 360° | octahedron | |
| 5 | 300° < 360° | icosahedron | |
| 6 | 360° = 360° | does not exist |
Next, consider a regular polyhedron with squares as its faces.
Since each interior angle of a square measures 90°, only three squares can meet at a vertex without exceeding the limit. If four did, the angle sum would be exactly 360°, which is not allowed: \(4 \times 90^\circ = 360^\circ\).
| Regular polygon | Number of faces meeting at a vertex | Sum of face angles | Polyhedron |
|---|---|---|---|
| squares (angles of 90°) |
3 | 270° < 360° | cube |
| 4 | 360° = 360° | does not exist |
Now let’s examine a regular polyhedron with regular pentagons as its faces.
Each angle in a regular pentagon is 108°. So at most three pentagons can meet at a vertex; four would give a total of \(4 \times 108^\circ = 432^\circ\), which clearly exceeds the threshold of 360° and is therefore impossible.
| Regular polygon | Number of faces meeting at a vertex | Sum of face angles | Polyhedron |
|---|---|---|---|
| pentagons (angles of 108°) |
3 | 324° < 360° | dodecahedron |
| 4 | 432° > 360° | does not exist |
Let’s now consider the case of a regular polyhedron made of regular hexagons.
Each interior angle in a regular hexagon is 120°. Even with just three faces meeting at a vertex, the sum would be \(3 \times 120^\circ = 360^\circ\), which hits the upper limit exactly - again making the construction of a solid angle, and thus a polyhedron, impossible.
| Regular polygon | Number of faces meeting at a vertex | Sum of face angles | Polyhedron |
|---|---|---|---|
| hexagons (angles of 120°) |
3 | 360° = 360° | does not exist |
At this point, there's no need to consider regular polygons with more than six sides - the angle sum at a vertex would only increase, making a solid impossible.
This confirms that only five regular polyhedra exist: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron.
Dihedral Angles of a Polyhedron
Each edge of a polyhedron is associated with a dihedral angle, which is formed by the two faces that meet at the edge.
For example, each edge of a cube is the intersection of two squares that lie on two different half-planes.
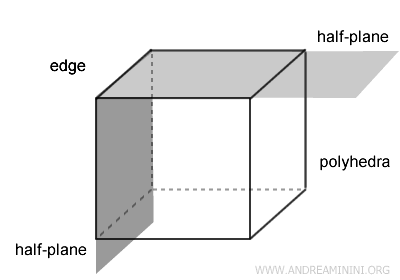
The dihedral angle associated with the edge is a dihedral angle of the polygon.
Net of a Polyhedron
The total surface area of a polyhedron is equal to the sum of the areas of its faces.
To study the total surface area of a polyhedron, the net of the polyhedron is often used, which is a 2D representation of the polyhedron.
The net of a polyhedron is a two-dimensional representation of the solid. It is created by "unfolding" the faces of the polyhedron into a flat figure.
The net allows us to see all the faces of the polyhedron in a single plane without any overlaps, preserving the proportions and connections between the faces.
This makes it easier and more intuitive to study the lateral and base surfaces of the polyhedron.
Example
The net of a cube is a cross-shaped figure composed of 6 squares, each representing one face of the cube.
Each side of the squares in the plane corresponds to an edge of the cube.
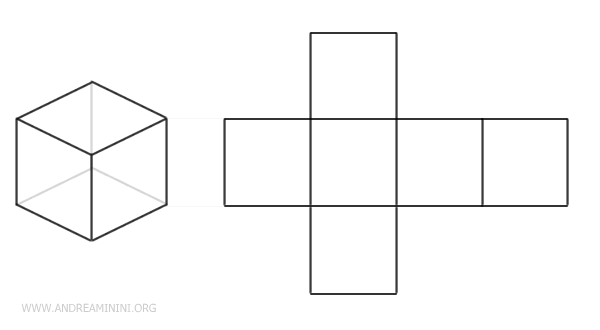
This is just one of the many possible ways to unfold a cube.
In the net of parallelepipeds, rectangular surfaces are used instead.
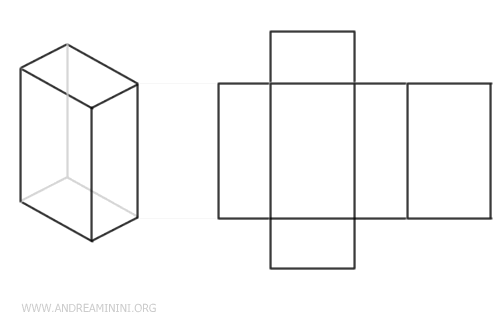
The central surfaces are the lateral faces of the parallelepiped, while the top and bottom surfaces are the bases.
And so on.
