Thales' Theorem in Space

A set of parallel planes \( \pi_1, \pi_2, \pi_3 \) intersects two transversal lines \( r \) and \( s \), dividing them into corresponding segments that are proportional.

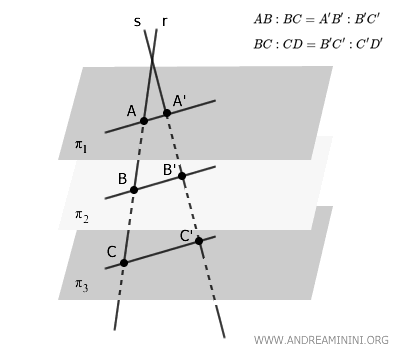
This theorem is simply the three-dimensional extension of the classic Thales' theorem in the plane.

In essence, Thales' theorem in space states that the ratio between segments formed by parallel planes remains the same across any pair of transversals, whether they are skew or coplanar.

Proof

Consider a set of parallel planes \( \pi_1, \pi_2, \dots, \pi_n \).

The proof consists of two cases: one for coplanar transversals and one for skew transversals.

1] Case of Coplanar Transversals

In this case, the two transversals \( r \) and \( s \) lie in the same plane.

The plane containing \( r \) and \( s \) intersects the parallel planes along parallel lines, forming the segments \( AA' \), \( BB' \), \( CC' \), and so on.

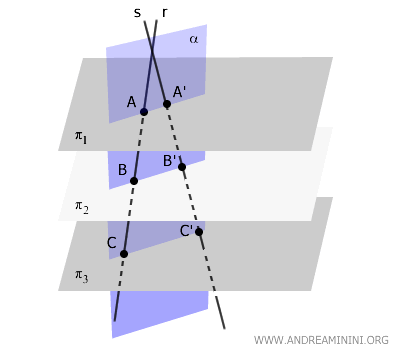
Since all the lines \( AA' \parallel BB' \parallel CC' \) are parallel and lie in the same plane \( \alpha \), which contains the transversals \( r \) and \( s \), they are coplanar.

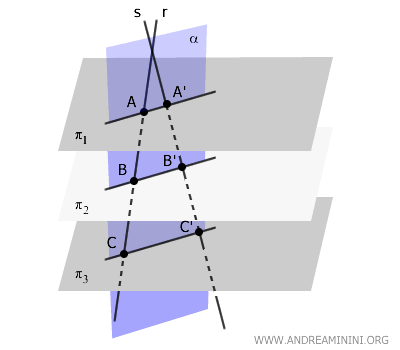
By applying Thales' theorem in the plane, we know that two transversals cutting through a family of parallel lines produce proportional segments:

$$ \frac{AB}{BC} = \frac{A'B'}{B'C'} $$

$$ \frac{BC}{CD} = \frac{B'C'}{C'D'} $$

$$ \frac{AC}{BC} = \frac{A'C'}{B'C'} $$

$$ ... $$

Similarly, the proportionality holds for any other pair of segments formed by the parallel planes.

Thus, Thales' theorem in space is proven for coplanar transversals.

2] Case of Skew Transversals

Now, let’s examine the case where \( r \) and \( s \) are skew lines.

The points where \( r \) intersects the parallel planes are labeled \( A, B, C, \) and so on, while the intersection points of \( s \) with the same planes are labeled \( A', B', C' \).

 

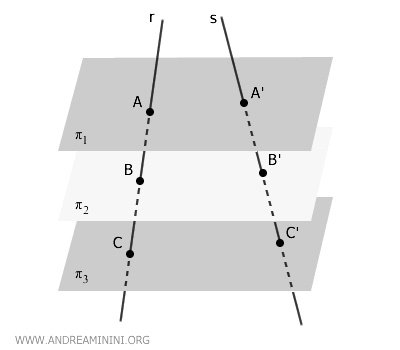
To bridge the gap between the two transversals, we introduce a new line \( r'' \) parallel to \( r \), passing through a point \( P \) on \( s \). This creates a plane containing both \( s \) and \( r'' \), allowing us to apply Thales' theorem in the plane.

The points where \( r'' \) meets the parallel planes are labeled \( A'', B'', C'' \).

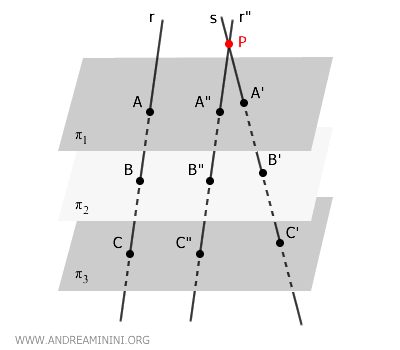
With this setup, the segments form parallelograms such as \( ABB''A'' \) and \( ACC''A'' \).

Since these are parallelograms, their opposite sides are parallel. This means \( AB \cong A''B'' \) and \( AC \cong A''C'' \), so they are equal in length.

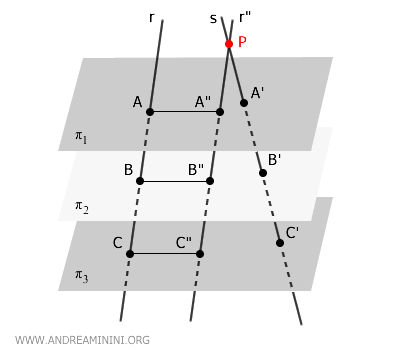
The transversals \( r'' \) and \( s \) intersect, meaning they lie in the same plane \( \alpha \) and are therefore coplanar.

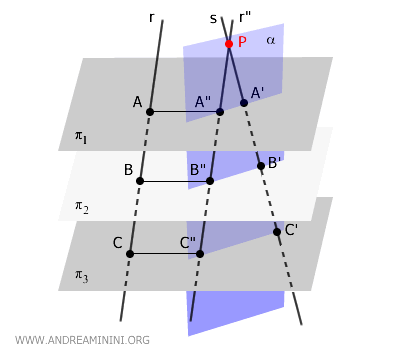
Since \( r'' \) and \( s \) are now coplanar, we can apply Thales' theorem in the plane to these transversals:

$$ \frac{A''B''}{B''C''} = \frac{A'B'}{B'C'} $$

$$ \frac{A''C''}{B''C''} = \frac{A'C'}{B'C'} $$

Given that \( AB \cong A''B'' \) and \( AC \cong A''C'' \), we conclude:

$$ \frac{AB}{BC} = \frac{A'B'}{B'C'} $$

$$ \frac{AC}{BC} = \frac{A'C'}{B'C'} $$

Thus, Thales' theorem in space holds even when the transversals are skew.

And so on.