Unfolding a Polyhedron

Unfolding a polyhedron means laying out its faces on a flat surface so that all of them are visible, arranged on a single plane, and don’t overlap.

In other words, this process turns the polyhedron into a two-dimensional model, keeping the dimensions, proportions, and connections between its faces intact.

This lets you represent a three-dimensional object (a polyhedron) on a flat surface.

This approach makes it easier and more intuitive to study the features of its lateral and base surfaces.

Note: Typically, the unfolding of a polyhedron is done by hand on paper for simpler shapes. However, with the advent of CAD (Computer-Aided Design) technology, it’s now possible to create unfoldings for more complex polyhedra and solids with greater precision and in less time. This is especially useful in architecture and design for planning structural and decorative elements, as well as in industrial settings for designing efficient packaging, and more.

Types of Polyhedra and Their Unfoldings

Many polyhedra have straightforward unfoldings, including cubes, rectangular prisms, pyramids, and regular prisms.

Other polyhedra have more complex unfoldings.

Cubes and Rectangular Prisms

These typically unfold into a rectangular or cross shape.

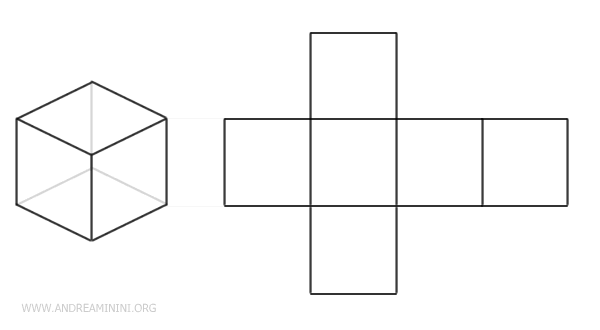
For example, a cube can be unfolded into a cross of squares.

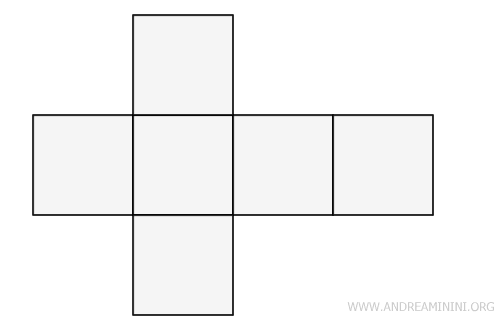
But that’s not the only way to unfold a cube. There are many other options.

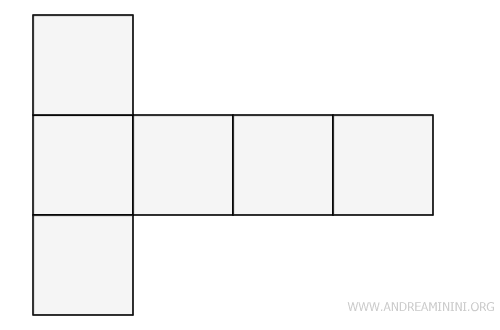
For instance, the T-shape is also a popular choice.

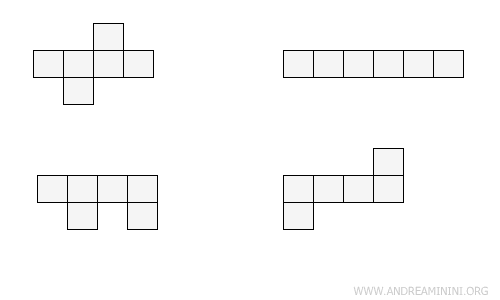
Beyond these, there are several other forms.

Rectangular prisms typically unfold into a rectangular shape.

The bases are usually shown on the top and bottom, with the lateral surfaces in between.

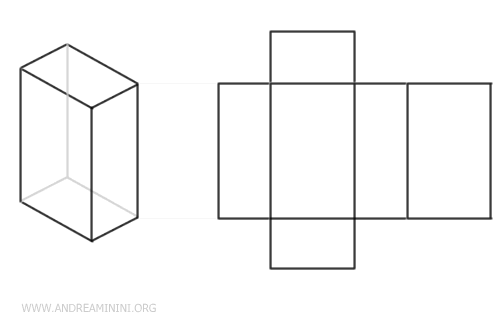
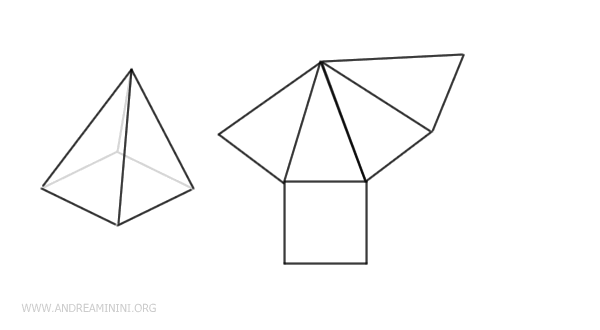
Pyramids

Pyramids usually unfold into a base with triangles that converge at a point.

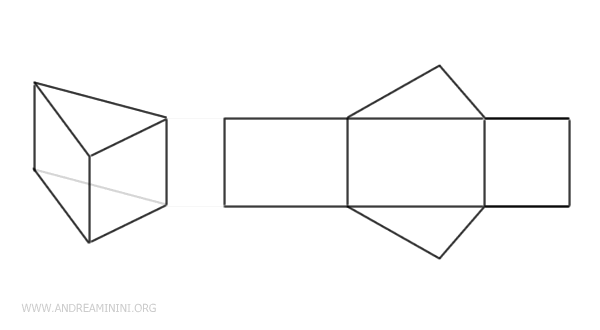
Prisms

The unfolding of a prism consists of two identical bases connected by rectangles or parallelograms.

Regular (Platonic) Polyhedra

These have symmetrical unfoldings, with each face represented by identical, regular shapes.

And so on.