Hyperboloid

A hyperboloid is a quadratic surface in three-dimensional space, appearing in two main forms: the hyperboloid of one sheet and the hyperboloid of two sheets, each defined by its own equation.

• Hyperboloid of one sheet
  The hyperboloid of one sheet is an infinitely extending surface resembling a "bottle neck" or saddle, also referred to as a "hyperbolic hyperboloid." Its general equation, a second-degree polynomial, is $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1 $$ where \(a\), \(b\), and \(c\) set the dimensions of the hyperboloid along the \(x\), \(y\), and \(z\) axes. Horizontal slices (where \(z\) is constant) are ellipses, while vertical slices (parallel to the \(x\) or \(y\) axes) are hyperbolas. This surface is continuous and unified.
  
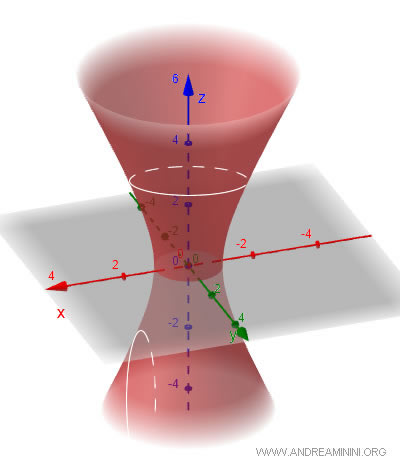
• Hyperboloid of two sheets
  The hyperboloid of two sheets features two distinct and opposite parts that symmetrically diverge from the center, often called an "elliptic hyperboloid." Its general equation is $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = -1 $$ Here, \(a\), \(b\), and \(c\) again determine the dimensions. Horizontal sections remain ellipses, whereas vertical sections form hyperbolas. However, unlike the hyperboloid of one sheet, it consists of two separate parts, thus it is not continuous or connected.
  

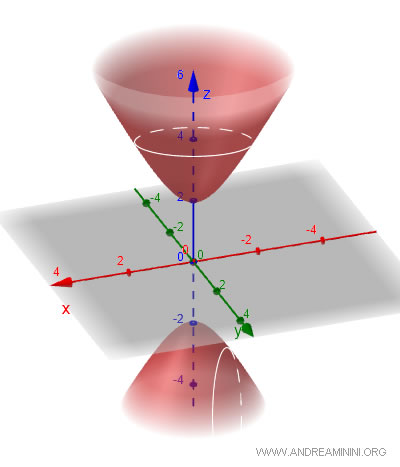
Hyperboloids are ruled surfaces, which means they can be generated through straight lines. This characteristic renders them particularly appealing for structural applications.

They are commonly used in architecture and engineering to craft structures that are both lightweight and robust, like towers, domes, or lattices.

And so forth.