Adding and Subtracting Solids
Solid geometry focuses on three-dimensional figures, known as solids, and the operations that can be performed on them. Among these operations, union and difference are fundamental tools for combining or removing volumes.
Union of Solids
The union of two solids A and B that do not share any interior points (that is, they are either disjoint or touch only at their boundaries) results in a new solid C consisting of all the points belonging to either A or B. $$ A + B = C $$
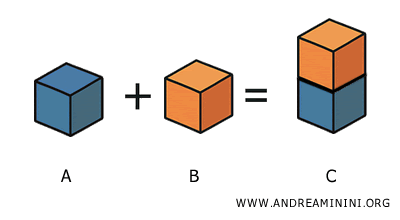
Solids A and B are referred to as components of the resulting solid C.
The union operation satisfies two fundamental properties:
- Commutativity: The order in which the solids are combined does not affect the outcome. $$ A + B = B + A = C $$
- Associativity: When combining more than two solids, the grouping of operations does not change the result. $$ (A + B) + C = A + (B + C) $$
These properties make union especially useful for decomposing and reconstructing complex shapes, which is particularly valuable in volume calculations and 3D modeling workflows.
Example
Consider two cubes - one with a side length of 3 cm, and the other 2 cm - placed close to each other without overlapping.
Their union, denoted as solid C, includes both cubes as distinct, non-overlapping parts.
The total volume is simply the sum of their individual volumes:
\[ V = 3^3 + 2^3 = 27 + 8 = 35\ \text{cm}^3 \]
Difference of Solids
The difference between two solids A and B is the solid C defined by: $$ C = A - B $$ That is, C represents the portion of A that remains after removing B.
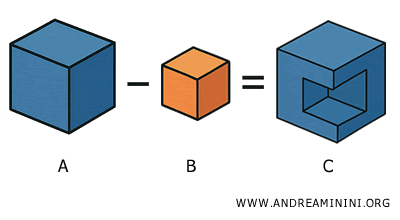
For the difference to be well-defined, solid B must lie entirely or partially within solid A.
Example
Take the same two cubes - one 3 cm per side, the other 2 cm.
This time, the smaller cube is embedded within the larger one, perfectly centered.
The resulting solid C = A − B is a hollow cube with a centered cavity. The remaining volume is:
\[ V = 3^3 - 2^3 = 27 - 8 = 19\ \text{cm}^3 \]
And so on.
