Extension of Solids
In solid geometry, the extension of a solid refers to the amount of space occupied by a three-dimensional object.
Unlike length or area, extension isn't something we measure directly. It's a primitive concept - an idea accepted without the need for a formal definition. We understand it intuitively through experience.
For example, when you look at a three-dimensional object - a box, a sphere, or a pyramid - the first thing you perceive is the space it fills, how "large" or "small" it seems.
This occupied space isn’t merely a physical measurement; it's a foundational idea that underlies the notions of volume, equivalence, and congruence between solids.
It's intuitive to recognize that two objects have the same extension if they occupy the same amount of space, even if their shapes differ.
Example. Pour a liter of water into a bottle, a cube, or a sphere, and each container will be completely filled. Although the shapes are different, the amount of space they occupy - their extension - is the same.
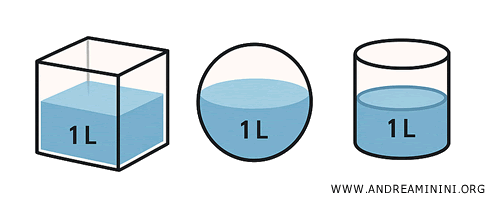
In geometry, we use volume to quantify and compare extensions. Crucially, volume depends solely on the amount of space occupied, not on the shape of the object.
Equivalence Between Solids
Two solids, A and B, are said to be equivalent solids if they have the same extension. $$ A \doteq B $$ Here, $ \doteq $ denotes equivalence.
This relationship is analogous to the equivalence relations we encounter in arithmetic and set theory, and it satisfies three fundamental properties:
- Reflexivity: Every solid is equivalent to itself.
- Symmetry: If A is equivalent to B, then B is equivalent to A.
- Transitivity: If A is equivalent to B and B is equivalent to C, then A is equivalent to C.
These properties characterize what we call an equivalence relation.
Thus, equivalence partitions solids into extension classes - sets of solids that occupy the same volume of space.
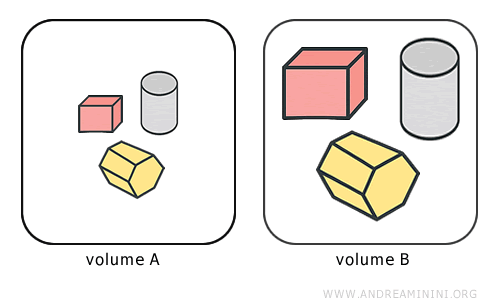
The volume serves as a numerical measure of a solid’s extension. Consequently, each extension class corresponds to a specific volume.
How to Determine If Two Solids Are Equivalent
A common method for comparing solids involves dividing them into smaller volume units and then reassembling them.
For instance, if you divide a solid into four smaller cubes, you can rearrange these cubes in various ways, fitting them together to form new shapes.
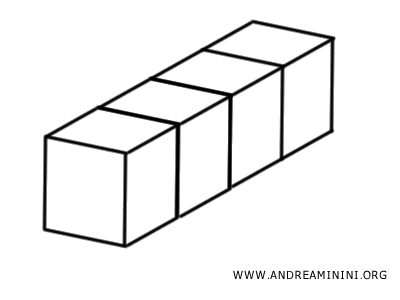
The resulting solid has the same extension as the original because no space has been added or removed - only reorganized. Therefore, the two solids are equivalent and have the same volume.
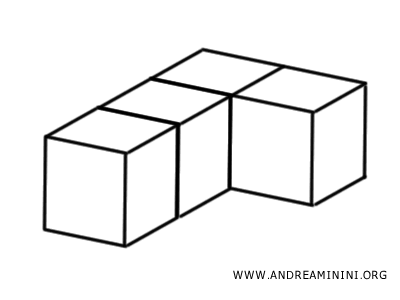
However, the shape of the new solid differs, meaning that the two solids are not congruent.
It's much like building with toy bricks: as long as you use the same number of bricks, the total volume stays the same, even though the final shapes may vary greatly.
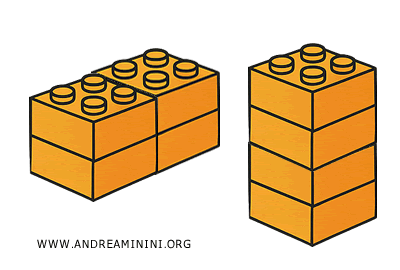
The Difference Between Congruence and Equivalence
Congruence and equivalence are distinct concepts:
- Congruent solids: These have identical shapes and sizes, and therefore are always equivalent.
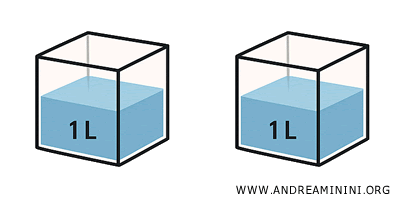
- Equivalent solids: These share the same volume but may differ in shape. For example, a cylinder and a prism can have identical heights and volumes but completely different forms. They are equivalent but not congruent.
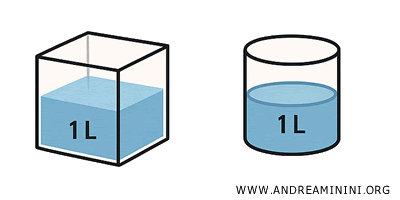
Grasping the concept of a solid’s extension is fundamental to understanding volume and to making meaningful comparisons between three-dimensional figures in geometry.
It's what allows us to assert that a one-liter bottle holds the same amount of liquid, regardless of the bottle's shape.
In short, extension isn’t directly visible; it is revealed through measurement of volume. Just as two differently shaped books might fit into the same shelf space, two distinct solids can occupy the same volume.
And so forth.
