A Solid Formed by Subtracting Two Cones from a Cylinder

This geometric solid is constructed by removing two identical cones from an equilateral cylinder that tightly encloses a sphere.

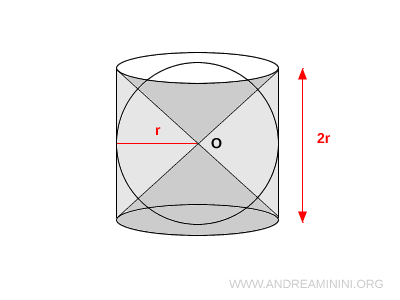
While it may appear simple, the resulting shape displays elegant geometric properties - particularly in its volume and symmetry.

How to Construct the Solid

Start with a sphere centered at point O with radius $R$.

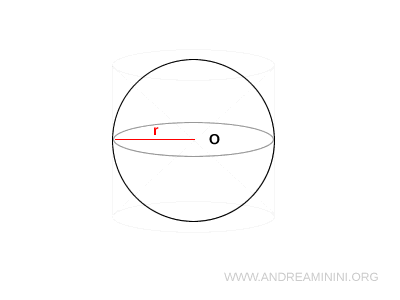
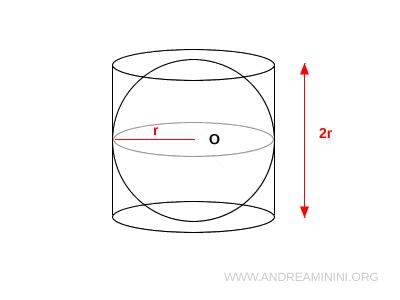
Enclose the sphere in an equilateral cylinder, meaning a cylinder whose height $h$ equals the diameter of its base $r$. Therefore:

• Height of the cylinder: $h = 2R$
• Radius of the base: $r = R$

Then, create two identical cones with their vertex at point O and bases coinciding with the cylinder’s top and bottom faces.

Each cone has:

• Height: $R$
• Base radius: $R$

Subtract the two cones from the volume of the cylinder.

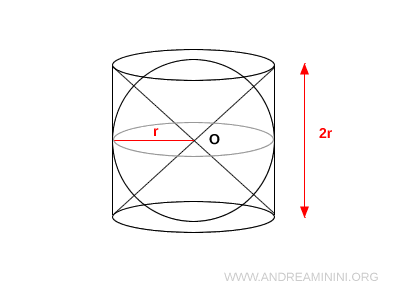
The final shape is a cylinder with its ends symmetrically carved out by two opposing cones - a surprisingly balanced and harmonious form.

Volume of the Solid

The cylinder-minus-two-cones solid has the same volume as the sphere inscribed in the cylinder.

The volume of the equilateral cylinder is:

$$ V_{\text{cyl}} = \pi R^2 \cdot 2R = 2\pi R^3 $$

The volume of a cone with base radius and height both equal to $R$ is:

$$ V_{\text{cone}} = \frac{1}{3} \pi R^2 \cdot R = \frac{1}{3} \pi R^3 $$

Since two cones are removed, the total volume subtracted is:

$$ 2 \cdot V_{\text{cone}} = \frac{2}{3} \pi R^3 $$

The resulting volume of the solid is:

$$ V_{\text{solid}} = V_{\text{cyl}} - 2 \cdot V_{\text{cone}} = 2\pi R^3 - \frac{2}{3} \pi R^3 = \frac{4}{3} \pi R^3 $$

Interestingly, this matches exactly the volume of a sphere of radius $R$:

$$ V_{\text{sphere}} = \frac{4}{3} \pi R^3 $$

Example

If the radius of the sphere is $R = 3$ cm, the volume of the solid is:

$$ V = \frac{4}{3} \pi (3)^3 = \frac{4}{3} \pi \cdot 27 = 36\pi \approx 113.1 \, \text{cm}^3 $$

This demonstrates a striking fact: although the solid is built from basic elements, its volume is exactly the same as that of the enclosed sphere - a surprising but mathematically rigorous result.

Note. This solid provides an excellent illustration of the volume comparison principle, which is foundational in integral calculus and dates back to the method of indivisibles developed by Archimedes. By decomposing solids into infinitesimal elements - such as slices or segments - and comparing them part by part, one can show that if each corresponding element in two solids has the same measure, then the total volumes must also be equal. This is the essence of Cavalieri’s Principle.

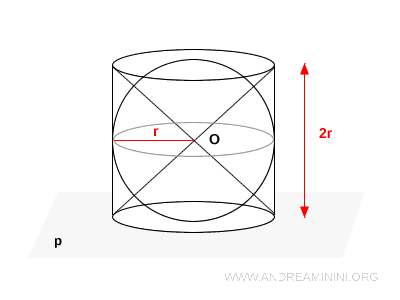
Proof

Consider a right circular cylinder of height $2r$ and radius $r$, resting on a base plane $p$. Inside the cylinder sits an inscribed sphere, and two identical cones whose common vertex is at point $O$ (the center of the sphere) and whose bases coincide with the bases of the cylinder.

Now slice the cylinder with a plane $p'$ parallel to the base, located at a vertical distance $h$ from the center $O$ of the sphere.

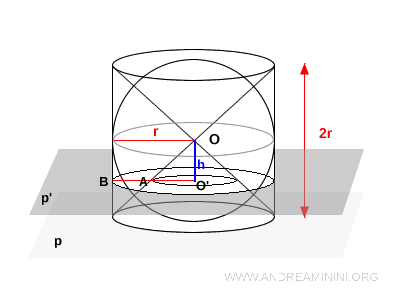
The intersection of plane $p'$ with one of the cones (i.e., the interior part removed from the cylinder) is a circle of radius $h$. This follows from triangle $OO'A$, which is a right isosceles triangle: since $OO' = O'A$ in a right circular cylinder, both legs equal $h$, so $O'A = h$.

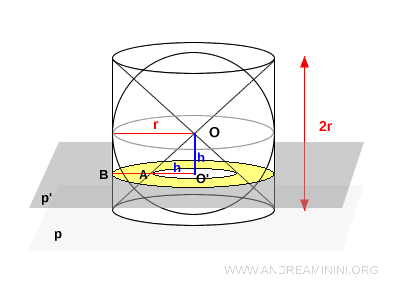
At height $h$, the horizontal cross-section of the cylinder-minus-two-cones solid is an annulus: the outer radius is $r$ (from the cylinder), and the inner radius is $h$ (from the cone).

The area of the annular section is:

$$ A_c = \pi r^2 - \pi h^2 = \pi (r^2 - h^2) $$

Now consider the inscribed sphere.

The same plane $p'$ intersects the sphere in a circle. The radius of this circle is $O'C$, where $C$ is a point on the sphere’s surface.

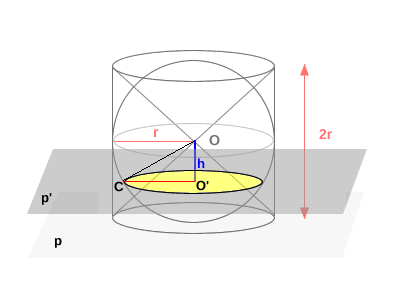
In triangle $O'OC$, which is right-angled at $O'$, we apply the Pythagorean Theorem:

$$ O'C^2 = OC^2 - OO'^2 = r^2 - h^2 $$

The area of the circle formed by the intersection of the sphere and the plane $p'$ is therefore:

$$ A_s = \pi \cdot O'C^2 = \pi (r^2 - h^2) $$

Thus, at every height $h$, the horizontal cross-section of the sphere has the same area as that of the cylinder-minus-two-cones solid.

By Cavalieri’s Principle, if two solids have the same height and identical cross-sectional areas at every level, they must have the same volume.

It follows that the cylinder-minus-two-cones solid and the sphere have equal volume.

And that completes the proof.

And so on.