Cone
A cone is a solid figure created by rotating a right triangle ABC around one of its legs, which serves as the axis of rotation.
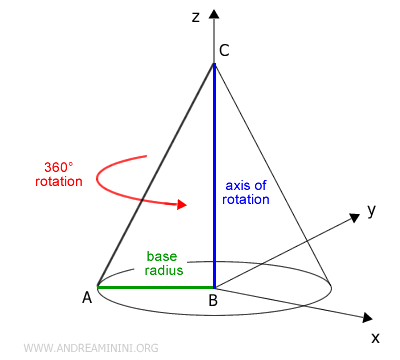
The leg chosen as the axis of rotation defines the height of the cone.
The other leg becomes the base radius of the cone, while the hypotenuse is known as the slant height.
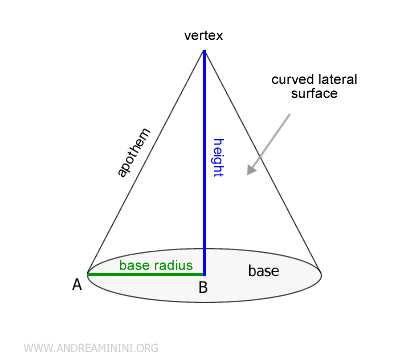
A cone consists of a circular base and a curved lateral surface.
The point where the height meets the lateral surface, opposite the base, is called the vertex of the cone.
The cone is one of the most recognized solids of revolution, along with the sphere and the cylinder.
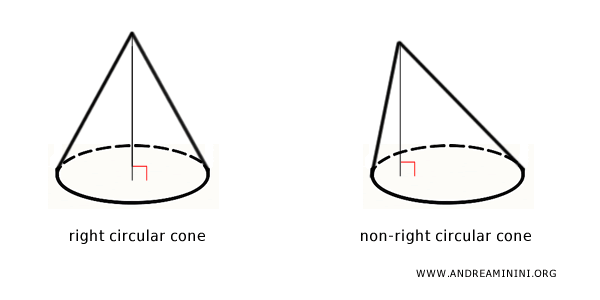
In basic geometry, when we talk about a cone, we usually refer to a right circular cone, which has a perfectly circular base and a perpendicular height. However, there are other types of cones, known as indefinite cones, such as the elliptical cone, oblique circular cone, quadratic cone, and more. So, the right circular cone is just one of many types of cones. There are also non-standard cones that cannot be generated by simply rotating a triangle around one of its sides. A typical example is the oblique cone, where the height does not coincide with the axis of rotation.
Formulas
Here are some key formulas for calculating various properties of a right circular cone:
The lateral surface area is given by the product of the base's semicircumference (πr) and the slant height.
$$ S_L = \pi r \cdot a $$
Where "r" is the base radius and "a" is the slant height (apothem) of the cone.

Base Area
The base of a right circular cone is a circle, so its area is the area of a circle with radius "r":
$$ S_B = \pi r^2 $$
Total Surface Area
The total surface area of a cone is the sum of its lateral surface area and the area of its base:
$$ S_T = S_L + S_B $$
$$ S_T = \pi r \cdot a + \pi r^2 $$
$$ S_T = \pi r \cdot (a + r) $$
Where "r" is the base radius and "a" is the slant height.
Volume of the Cone
The volume of a cone is one-third of the volume of a cylinder with the same base and height:
$$ V = \frac{1}{3} \pi r^2 \cdot h $$
Where "r" is the base radius and "h" is the height.
Note. Based on the volume equivalence theorem for cones and pyramids, the volume is given by $$ V = \frac{1}{3} \cdot A \cdot h = \frac{1}{3} \pi r^2 h $$
Types of Cones
Cones can be categorized based on different geometric features. Here are some of the main types:
- Right Circular Cone
The most common type of cone, characterized by a circular base and a height extending from the vertex to the center of the base. In this cone, the axis is perpendicular to the base. - Oblique Circular Cone
Similar to the right circular cone, but with the axis tilted relative to the base, so the vertex is not directly above the center of the base. - Elliptical Cone
This cone has an elliptical base instead of a circular one. The axis can be either perpendicular or oblique to the base. - Parabolic Cone
A solid formed by rotating a parabola around its axis. Unlike circular cones, it does not have a well-defined circular base. - Hyperbolic Cone
Formed by rotating a hyperbola around its axis, this cone has two separate, symmetrical parts. - Spherical Cone
A solid formed by rotating a semicircle around its diameter, which is also the height of the cone. It has a circular base and a curved surface that meets at the vertex, similar to a spherical cap.
These are just a few examples of the types of cones you might encounter in geometry.
Cone in Analytic Geometry
In analytic geometry, a cone is a type of quadric surface that can be represented by an equation in Cartesian coordinates.
General Equation of a Cone
This general equation can represent different types of cones, including non-circular ones, depending on the values of a, b, and c:
$$ \begin{pmatrix} \frac{x}{a} \end{pmatrix} ^2 + \begin{pmatrix} \frac{y}{b} \end{pmatrix} ^2 - \begin{pmatrix} \frac{z}{c} \end{pmatrix} ^2 = 0 $$
Where x, y, and z are the coordinates of points (x;y;z) in three-dimensional Cartesian space.
Equation of a Right Circular Cone
The most common form of a cone in analytic geometry is the right circular cone, with the standard equation:
$$ x^2 + y^2 = z^2 \cdot \begin{pmatrix} \frac{r}{h} \end{pmatrix}^2 $$
Where r is the radius of the base of the cone and h is the height. The ratio r/h determines the slope of the cone’s surface.
This equation represents a cone with its vertex at the origin (x;y;z)=(0;0;0) in the Cartesian plane, the axis of rotation along the z-axis, and a circular base in the xy-plane.
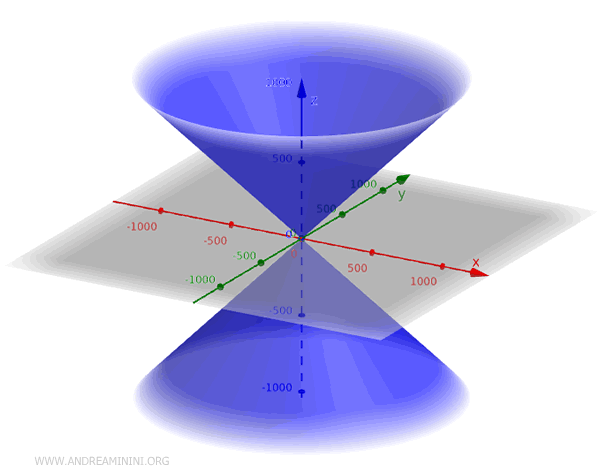
The standard equation usually represents a double cone extending both above and below the xy-plane.
To restrict the cone to just one of these regions, additional conditions must be applied to the equation.
For example, intersecting the cone with a plane parallel to the xy-plane at a certain height, and the condition z>0.
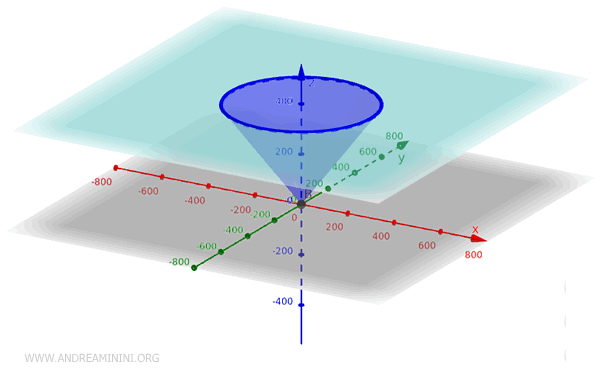
Note: The equations for a cone can vary depending on its orientation and position in space. For example, by modifying the standard equation, you can create cones with vertices at points other than the origin or with axes aligned along the x- or y-axes.
Right Circular Conical Surface
The equation of a conical surface with its vertex at the origin $ O $ of the Cartesian coordinate system, an axis aligned with the z-axis, and a half-angle $ \delta $ is: $$ x^2 + y^2 - k^2 z^2 = 0 $$ where $ k^2 = \tan^2 \delta $.
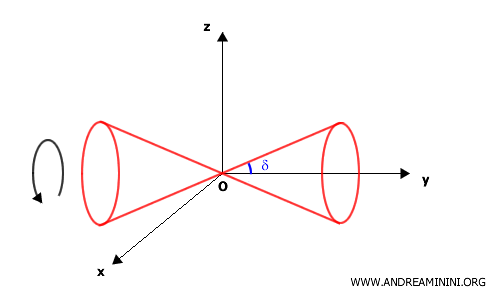
If the axis of the conical surface lies along the x-axis, the equation becomes:
$$ y^2 + z^2 - k^2 x^2 = 0 $$
Similarly, if the axis lies along the y-axis, the equation is:
$$ x^2 + z^2 - k^2 y^2 = 0 $$
with $ k^2 = \tan^2 \delta $ in each case.
Proof
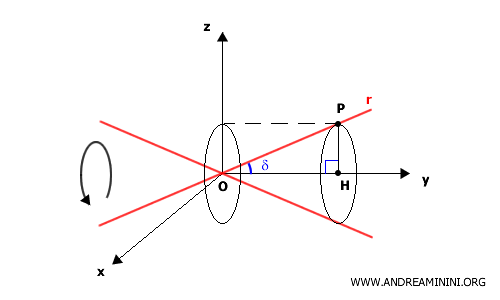
Consider a line $ r $ passing through the origin $ O $, forming an angle $ \delta $ with respect to the y-axis.
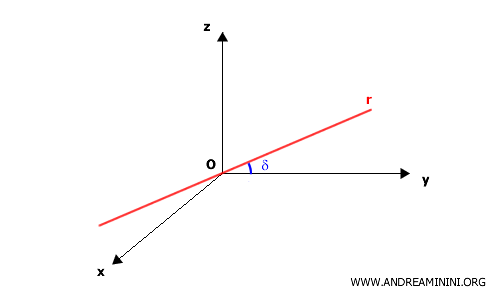
This line is known as a generator of the cone, because rotating it around the y-axis sweeps out the conical surface.
Let $ P(x, y, z) $ be a point on the line $ r $, and let $ H $ be its orthogonal projection onto the y-axis.
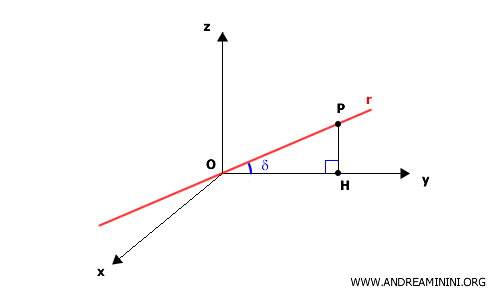
The triangle $ OPH $ is a right triangle, with one acute angle equal to $ \delta $.
If we consider the hypotenuse $ OP $, the leg $ OH $ represents the projection of $ OP $ onto the y-axis and is given by:
$$ OH = |OP| \cdot \cos \delta $$
The segment $ PH $ is the leg opposite the angle $\delta$, and it can be expressed as:
$$ PH = |OP| \cdot \sin \delta $$
In particular, if we choose $ |OP| = 1 $, then:
$$ OH = \cos \delta $$
$$ PH = \sin \delta $$
Therefore, the tangent of angle $ \delta $ is:
$$ \tan \delta = \frac{ \sin \delta }{ \cos \delta } = \frac{PH}{OH} $$
Since the length of segment $ OH $ is $ |y| $, it follows that:
$$ \tan \delta = \frac{PH}{|y|} $$
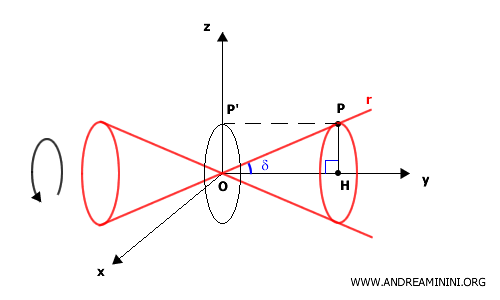
The segment $ PH $ represents the radius of a circle whose projection onto the xz-plane has its center at the origin $ O $ and radius $ OP' $. The equation of this circle is $ x^2 + z^2 = OP'^2 $.
Since $ OP' = PH $, we can write the circle’s equation as $ x^2 + z^2 = PH^2 $. Therefore, we have: $$ PH = \sqrt{x^2 + z^2} $$
Substituting $ PH = \sqrt{x^2 + z^2} $ into the equation $ \tan \delta = \frac{PH}{|y|} $ yields:
$$ \tan \delta = \frac{\sqrt{ x^2 + z^2 }}{|y|} $$
Squaring both sides and simplifying gives:
$$ (\tan \delta )^2 = \left( \frac{\sqrt{ x^2 + z^2 }}{|y|} \right)^2 $$
$$ \tan^2 \delta = \frac{x^2 + z^2}{y^2} $$
$$ y^2 \tan^2 \delta = x^2 + z^2 $$
$$ x^2 + z^2 - y^2 \tan^2 \delta = 0 $$
By letting $ k^2 = \tan^2 \delta $, the equation can be written as:
$$ x^2 + z^2 - k^2 y^2 = 0 $$
This proves the equation of the conical surface with half-angle $ \delta $ around the y-axis.
Additional Notes
Here are some additional points about cones:
- Equilateral Cone
A cone is called equilateral when the slant height (a) is equal to the diameter d=2r of the base. $$ a = 2r $$ Where "r" is the base radius of the cone. The intersection of an equilateral cone with a plane that contains the height of the cone forms an equilateral triangle. - Frustum of a Cone
A frustum of a cone is a solid obtained by cutting a cone with a plane parallel to its base, removing the upper portion. This solid has two circular bases of different diameters: a larger one (the original base of the cone) and a smaller one (the section where the cut was made). - Conic Sections
The intersections of a cone with planes can produce various conic sections, such as ellipses, parabolas, and hyperbolas, depending on the angle and position of the cutting plane.
And so on.
