Prisms

A prism is a polyhedron characterized by two parallel and congruent faces, known as bases, with all other faces being parallelograms.

The prism is a fundamental solid shape in spatial geometry.

Key Characteristics of a Prism

The parallel and congruent faces are called the prism's bases. These bases can have any shape.

Each edge of the bases is referred to as a base edge.

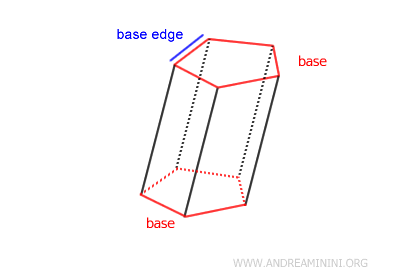
The shape of the bases determines the name of the prism. For example, a prism with triangular bases is known as a triangular prism. If the bases are quadrilateral, it's called a quadrangular prism; with five sides, it's a pentagonal prism; with six, a hexagonal prism, and so on. If the bases are regular polygons, the prism is called a regular prism. Otherwise, it is called "irregular."

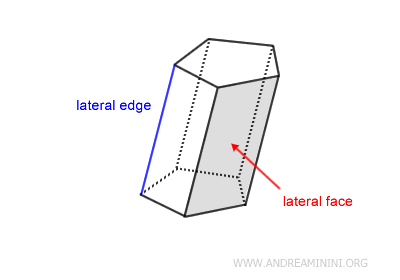
The other faces, known as lateral faces, are parallelograms that connect the corresponding vertices of the bases.

The segment that connects two vertices from different bases is called a lateral edge.

In a prism, all lateral edges are congruent.

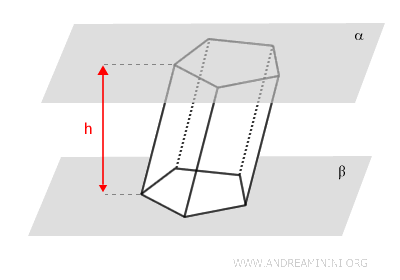
The distance between the two bases is known as the prism's height.

The diagonals of the prism are the segments connecting vertices that do not lie on the same base.

Types of Prisms

Prisms can be classified based on the shape of their bases:

• Triangular Prism
  Has triangular bases.
• Quadrangular Prism
  Has quadrilateral bases.
• Pentagonal Prism
  Has pentagonal bases.
  
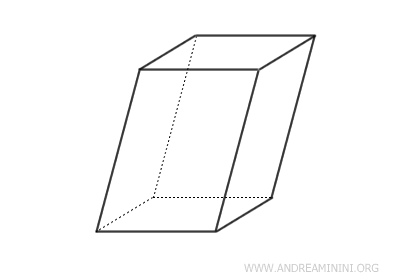
• Parallelepiped
  A parallelepiped is a prism whose bases are parallelograms.
  

And so on, for any other polygonal base.

Additionally, prisms can be classified based on the orientation of their lateral faces:

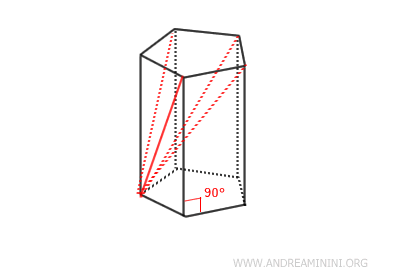
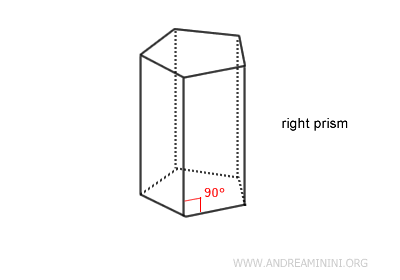
• Right Prism
  The lateral faces are rectangles, and the angle between the base and the lateral faces is 90 degrees. In a right prism, the lateral edges (i.e., the edges connecting the corresponding vertices of the two bases) are perpendicular to the planes of the bases. This means that these lateral edges are also the height of the prism.
  
• Oblique Prism
  The lateral faces are parallelograms, but not rectangles.
  
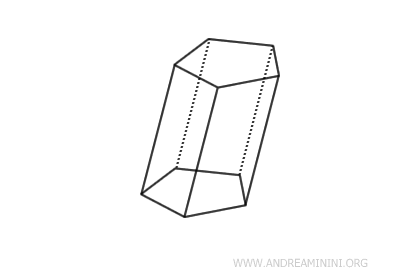
• Unbounded Prism
  An unbounded prism is a geometric figure formed by a polygon and a set of lines that are all parallel to a given line \( r \), which does not lie in the polygon’s plane. This structure extends infinitely in both directions along these parallel lines, creating an endless three-dimensional shape.
  
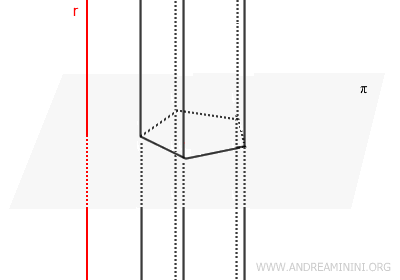
• Bounded Prism
  A bounded prism, commonly referred to simply as a prism, is a polyhedron formed by cutting an unbounded prism with two parallel planes. It consists of two congruent polygonal bases and lateral faces that are parallelograms.
  

Volume and Surface Area of a Prism

The volume of a prism is calculated by multiplying the area of the base A by the height h of the prism: $$ V = A \cdot h $$

The total surface area S of a prism is the sum of the areas of the two bases plus the areas of the lateral faces.

If P is the perimeter of the base and h is the height of the prism, the area of the lateral faces is P h. Therefore, the total surface area is:

$$ S = 2A + P \cdot h $$

Right Prism

A right prism is a type of prism where the lateral edges are perpendicular to the bases.

In a right prism, the lateral faces are rectangles, and the height of the prism is the same as the length of the lateral edges.

Notes

Additional remarks, theorems, and personal observations on the geometry of prisms.

• Prism Equivalence Theorem
  Two prisms have the same volume if their bases have equal area and their heights are congruent.

  Proof. Consider two prisms - not necessarily congruent - lying on the same plane $ \pi $. By hypothesis, both solids have bases of equal area, $ \text{Area}(ABC) = \text{Area}(ABCD) $, and the same height $ AH $.
  
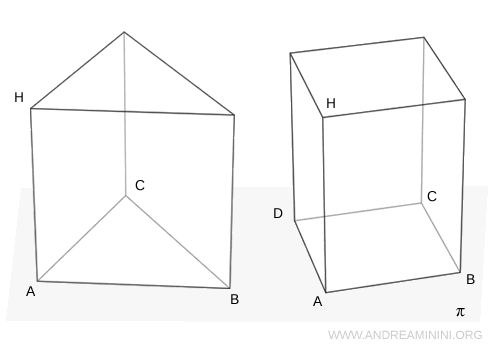
  Let $ \pi' $ be any plane parallel to the base that intersects both prisms. The resulting cross-sections - $A'B'C'$ and $A'B'C'D'$ - are congruent to their respective bases. This follows from the definition of a prism, where corresponding vertices are connected by segments that are both parallel and equal in length to the height.
  
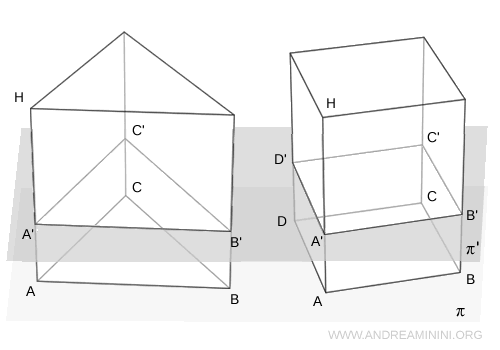
  Since every plane $ \pi' $ parallel to the base yields cross-sections of equal area, by Cavalieri’s Principle, the two solids must have the same volume. Hence, the two prisms are volume-equivalent solids.

• If two prisms have congruent bases, their volumes are proportional to their heights.

  Proof. The volume $V$ of any prism is calculated by multiplying the area of its base by its height - that is, the perpendicular distance between the two bases: $$ V = A_B \cdot h $$ where $A_B$ represents the area of the base and $h$ is the height of the prism. Now, if two prisms have congruent bases (i.e., equal base area $A_B$) and the same volume, they must also have the same height: $$ V_1 = V_2 \quad \text{and} \quad A_{B_1} = A_{B_2} \quad \Rightarrow \quad h_1 = h_2 $$ Conversely, if the two prisms share the same base area but differ in volume, then their volumes are directly proportional to their heights: $$ \frac{V_1}{V_2} = \frac{A_B \cdot h_1}{A_B \cdot h_2} = \frac{h_1}{h_2} $$ In short, when the base is fixed, a prism’s volume scales linearly with its height.

And so on.