Parallelepiped
A parallelepiped is a type of prism where the bases are parallelograms.
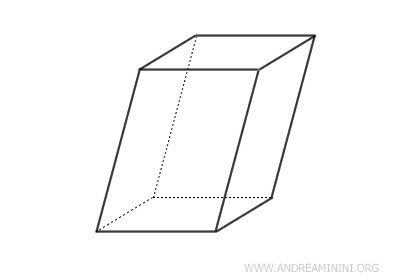
It’s a solid with 6 faces, each of which is a parallelogram, along with 12 edges and 8 vertices.
A parallelepiped has the following properties:
- Opposite faces are parallel and congruent.
- Opposite edges are parallel and congruent.
- Opposite vertices lie on parallel lines.
The lengths of the three edges meeting at any vertex are referred to as the dimensions of the parallelepiped.
The study of parallelepipeds dates back to ancient Greece, with mathematicians like Euclid writing about their properties and characteristics.
Types of Parallelepipeds
There are different types of parallelepipeds depending on the nature of their faces.
- Right Parallelepipeds
A right parallelepiped has rectangles for its lateral faces.

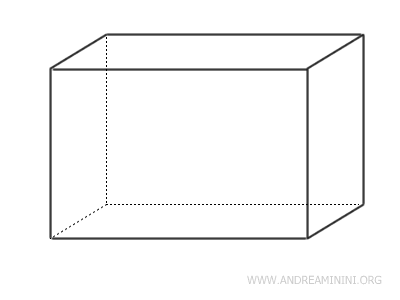
- Rectangular Parallelepipeds
A rectangular parallelepiped has rectangular bases, making all its faces rectangles.
- Oblique Parallelepipeds
In an oblique parallelepiped, the lateral faces are not rectangles. At least one of the faces is a rhombus or another type of parallelogram.
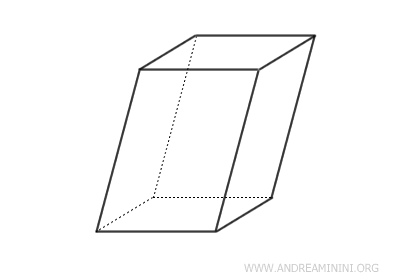
In solid geometry, the following specific types of parallelepipeds are quite common:
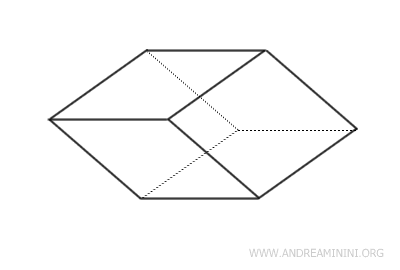
- Rhombohedron
A rhombohedron is a parallelepiped where all six faces are congruent rhombi.
- Cube
A cube is a parallelepiped where all six faces are congruent squares. It is a special case of both a rectangular parallelepiped and a rhombohedron.
Formulas for Parallelepipeds
As with any prism, the volume V of a parallelepiped is found by multiplying the area of one of its bases AB by its height h.
$$ V = A_B \cdot h $$
Rectangular Parallelepiped
In a rectangular parallelepiped, where the base dimensions are l (length), w (width), and h (height):
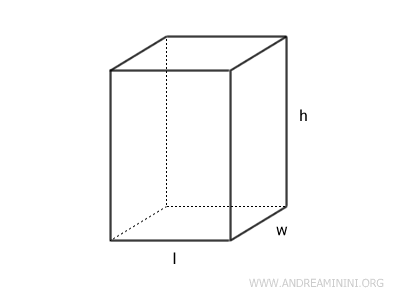
The volume V is given by multiplying the three dimensions:
$$ V = l \cdot w \cdot h $$
Here, AB=l·w represents the area of the base.
$$ V = A_B \cdot h $$
This is because a rectangular prism is a specific type of prism.
The lateral surface area SL of a rectangular parallelepiped is found by multiplying the perimeter of the base, 2(w+l), by the height h.
$$ S_L = 2 \cdot (w + l ) \cdot h $$
Where PB=2(w+l) is the perimeter of the base.
$$ S_L = P_B \cdot h $$
Alternatively, the lateral surface area can also be calculated by summing the areas of the lateral faces:
$$ S_L = 2 \cdot (w \cdot h + l \cdot h) $$
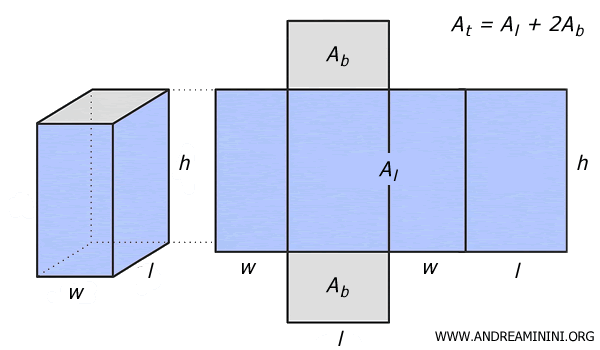
The total surface area ST of a parallelepiped is the sum of the areas of all six faces. It can be expressed as the lateral surface area SL=2(w+l)h plus twice the base area 2lw:
$$ S_T = 2(w+l)h + 2lw $$
$$ S_T = 2lw + 2lh + 2wh $$
Note. Keep in mind that the total surface area $ A_t $ is the sum of the lateral area $ A_l $ and twice the base area $ A_b $. Once you look at the unfolded shape of the rectangular prism, the logic behind the formula becomes much clearer.
The diagonal (d) of a rectangular parallelepiped is calculated as the square root of the sum of the squares of its dimensions:
$$ d = \sqrt{l^2+w^2+h^2} $$
Rectangular Parallelepiped
A rectangular parallelepiped is a three-dimensional solid in which both the bases and the lateral faces are rectangles.
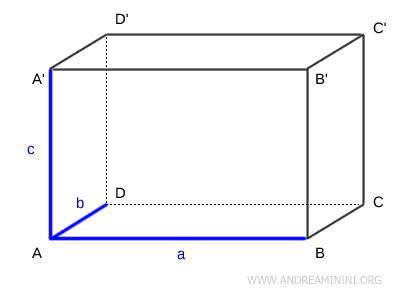
The dimensions of a parallelepiped are the lengths of the three edges that meet at a common vertex, denoted as \( a, b, c \).
Note. The concept of dimensions is particularly intuitive and widely used in the case of a rectangular parallelepiped, where the edges are mutually perpendicular, making the geometry straightforward and easy to measure. For instance, the lengths of the diagonals can be determined using the Pythagorean theorem. In a general parallelepiped, dimensions still exist, but calculations involving edge lengths and diagonals become more complex, as the edges are not necessarily perpendicular. In such cases, the angles between edges must also be taken into account.
The diagonal of the parallelepiped, denoted as \( d \), is the line segment connecting two opposite vertices.
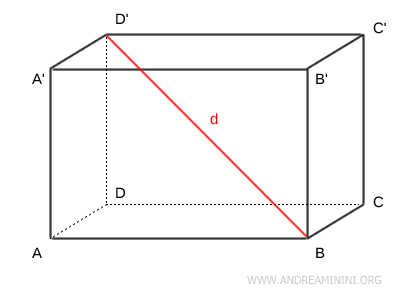
In a rectangular parallelepiped, all space diagonals are congruent.
The formula for calculating the length of the space diagonal takes into account all three dimensions of the solid:
\[ d = \sqrt{a^2 + b^2 + c^2} \]
This formula provides the maximum possible distance between two opposite vertices.
Proof. To derive this formula, consider the space diagonal \( d \) of the parallelepiped and the diagonal \( d_b \) of the rectangular base ABCD.
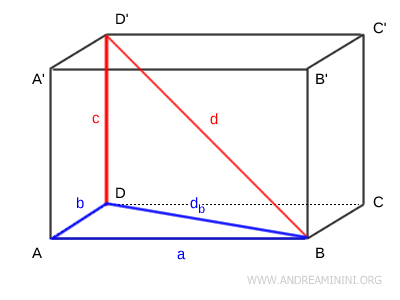
Applying the Pythagorean theorem to right triangle \( ABD \), which is formed by two adjacent sides of the base, we obtain the length of the base diagonal \( d_b \): \[ d_b^2 = a^2 + b^2 \] \[ d_b = \sqrt{a^2 + b^2} \] Next, we apply the Pythagorean theorem again to right triangle \( DBD' \), where the base diagonal \( d_b \) and the height \( c \) serve as the legs: \[ d^2 = d_b^2 + c^2 \] Substituting \( d_b^2 = a^2 + b^2 \) gives: \[ d^2 = (a^2 + b^2) + c^2 \] \[ \sqrt{d^2} = \sqrt{a^2 + b^2 + c^2} \] \[ d = \sqrt{a^2 + b^2 + c^2} \] Hence, the formula for the space diagonal of a rectangular parallelepiped is: \[ d = \sqrt{a^2 + b^2 + c^2} \] .
Observations and Notes
Here are a few additional notes on parallelepipeds:
- Opposite faces of a parallelepiped are congruent and parallel
The opposite surfaces of a parallelepiped, those that do not share vertices, are both congruent and parallel.
- The diagonals of a parallelepiped all intersect at a common point, where they bisect each other into two congruent segments.
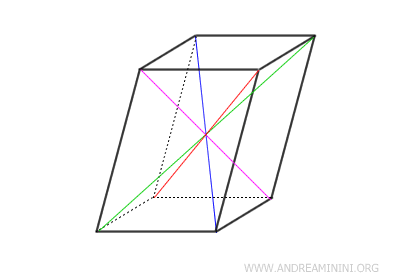
Proof. In this parallelepiped, the quadrilateral $ ABC'D' $ forms a parallelogram since its opposite sides are both congruent and parallel. Consequently, its diagonals $ AC' $ and $ BD' $ intersect at their midpoint $ O $, which implies that $ OA \cong OC' \cong OB \cong OD' $.
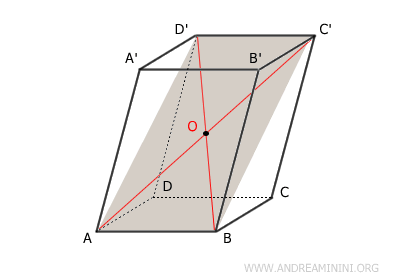
Likewise, the quadrilateral $ BCD'A' $ is also a parallelogram, as it shares the same property of having opposite sides that are congruent and parallel. Thus, its diagonals $ BD' $ and $ A'C' $ intersect at their midpoint $ O $, where they bisect each other, yielding $ OB \cong OC \cong OA' \cong OD' $. The point $ O $ is the same as in the previous case $ ABC'D' $ because the segment $ BD' $ is shared between both configurations.
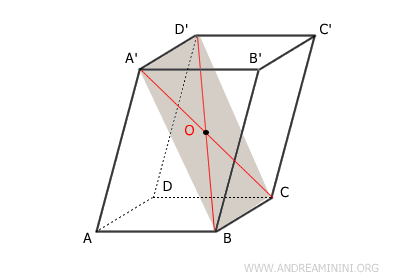
By applying the same reasoning to the remaining diagonals of the parallelepiped, we arrive at the same result: all diagonals bisect one another at a common midpoint $ O $, dividing each into two congruent segments. - In a rectangular parallelepiped, all the diagonals are congruent.
- If two rectangular prisms have congruent bases $ A_B $, then their volumes are directly proportional to their heights: $$ \frac{V_1}{V_2} = \frac{A_B \cdot h_1}{A_B \cdot h_2} = \frac{h_1}{h_2} $$
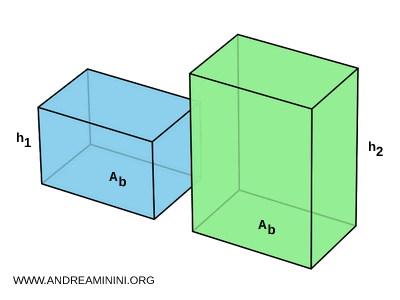
Proof. The volume $ V $ of a rectangular prism is given by the product of its three dimensions: $$ V = l \cdot w \cdot h $$ Since the base area is $ A_B = l \cdot w $, this simplifies to: $$ V = A_B \cdot h $$ Now, if two prisms have identical base areas (i.e., congruent bases) and equal volumes, then their heights must also be equal: $$ V_1 = V_2 \quad \text{and} \quad A_{B_1} = A_{B_2} \quad \Rightarrow \quad h_1 = h_2 $$ Conversely, if their base areas are the same but their volumes differ, then the ratio of their volumes matches the ratio of their heights: $$ \frac{V_1}{V_2} = \frac{A_B \cdot h_1}{A_B \cdot h_2} = \frac{h_1}{h_2} $$ In other words, when the base is fixed, the volume of a rectangular prism scales linearly with its height.
And so on.
