Opposite Faces of a Parallelepiped are Congruent and Parallel
Using Euclidean geometry, we can prove that the opposite faces of a parallelepiped are both congruent and parallel.
Proof
A parallelepiped is a solid with six faces, all of which are parallelograms.
Let’s consider a parallelepiped with vertices labeled \( A, B, C, D, A', B', C', D' \), where \( ABCD \) is one face, \( A'B'C'D' \) is its opposite face, and the remaining four faces are also parallelograms.
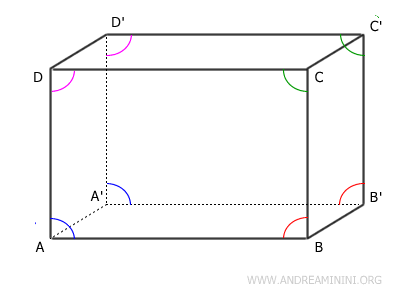
By definition, a parallelepiped has opposite edges that are equal in length:
\( AB = A'B' \)
\( BC = B'C' \)
\( CD = C'D' \)
\( DA = D'A' \)
Furthermore, the corresponding angles in opposite faces are equal, since each face is a parallelogram and maintains congruent internal angles.
Since the two faces share the same side lengths and angles, they are congruent by the parallelogram congruence criterion:
$$ ABCD \cong A'B'C'D' $$
The same reasoning applies to every pair of opposite faces in the parallelepiped.
Proof of Parallelism
Two planes are parallel if they never intersect and if one can be mapped onto the other by a translation.
For a parallelepiped:
- Each pair of opposite faces is separated by a uniform distance, meaning the planes remain equidistant at all points.
- The edges of opposite faces are parallel to one another.
Therefore, opposite faces lie in parallel planes, confirming their parallelism.
For instance, since the opposite faces $ ABCD \cong A'B'C'D' $ are congruent, the faces $ AA'D'D || BB'C'C $ must be parallel because their respective planes are equidistant, with $ AB \cong A'B' \cong CD \cong C'D' $. The same holds for all opposite faces of the parallelepiped.
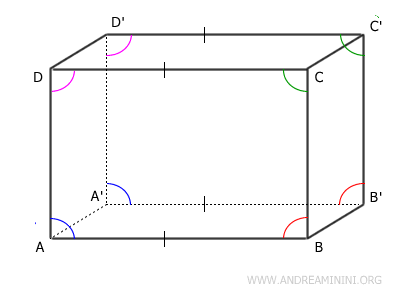
Conclusion
We have demonstrated that the opposite faces of a parallelepiped are congruent, as they have identical side lengths and angles, and that they are parallel because they reside in distinct, non-intersecting planes that are translations of one another.
This property holds for all parallelepipeds, including cubes and rectangular prisms.
And so forth.
