Solids of Revolution

A solid of revolution is formed when a plane figure rotates around a fixed line, called the axis of rotation, generating a surface in space.

As the plane figure rotates, it creates a symmetrical three-dimensional object, with its shape depending on the original figure and the axis chosen.

The surface that bounds the solid is known as the surface of revolution, and each point on the figure traces a circle as it rotates.

We refer to solids of revolution with angle α when the rotation is incomplete, meaning the rotation angle is less than 360° (a full circle). A solid of revolution with angle alpha is a partial or incomplete solid, like a sector of a cylinder or a sphere. If the angle isn't specified, it’s understood that the solid is formed by a full 360° rotation around an axis.

A Practical Example

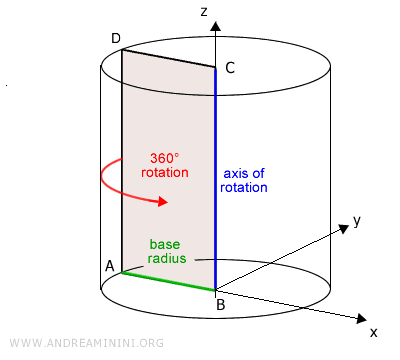
Let’s take a plane figure, like a rectangle ABCD.

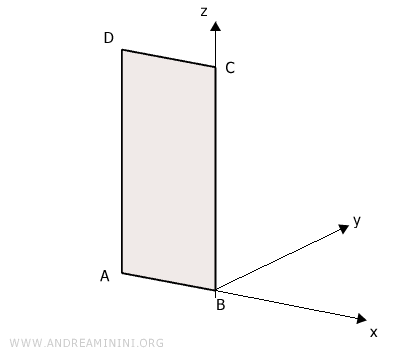
We’ll choose side BC of the rectangle, perpendicular to the plane, as the axis of rotation and rotate it through 360° (a full circle).

After completing the rotation, we’ve created a solid object, which in this case is a cylinder.

Types of Solids of Revolution

There are various types of solids of revolution, depending on the initial plane figure.

The main types include:

• Cylinder
  Formed by the complete rotation of a rectangle.
  
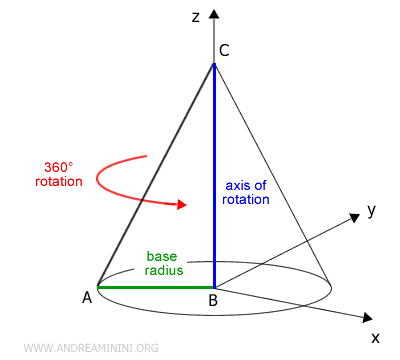
• Cone
  Formed by the complete rotation of a right triangle.
  
• Sphere
  Formed by the complete rotation of a semicircle around its diameter as the axis.
  

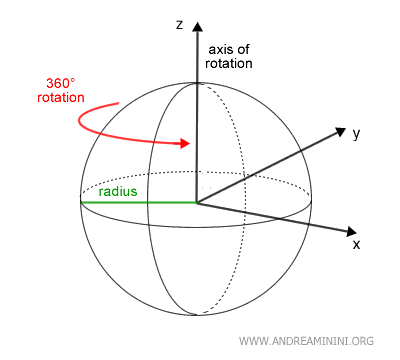
All solids of revolution are characterized by both axial and rotational symmetry around the axis of rotation.

And so on.