Cube

A cube is a rectangular parallelepiped (polyhedron) consisting of six identical square faces, all with right angles and equal edges.

Each of the cube's six faces is a perfect square. 

For this reason, the cube is also known as a regular hexahedron.

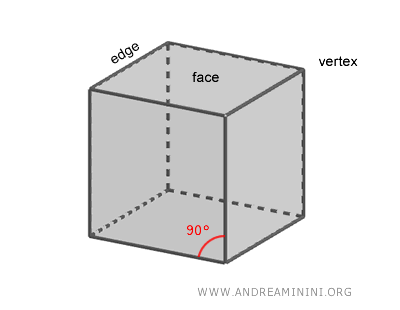
The word "hexahedron" comes from the Greek, where "hexa" means "six" and "hedron" means "face" or "base." The term "regular" refers to the fact that each face of the cube is a regular polygon, meaning all sides are congruent.

Geometrically speaking, a cube is a special type of rectangular prism where all three dimensions—length (l), width (w), and height (h)—are equal.

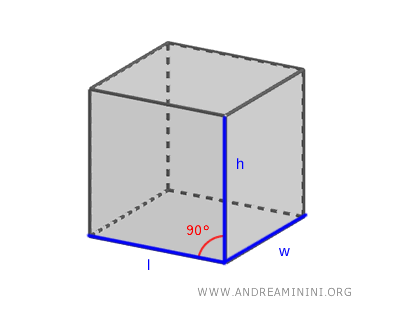
Each face of the cube is connected to four others by its edges, resulting in a total of 12 equal edges.

Additionally, the cube has 8 vertices, with three edges and three mutually perpendicular faces meeting at each vertex.

This feature gives the cube its unique stability and symmetry. Its shape is a perfect example of balance, making it one of the most studied shapes in geometry. As one of the five Platonic solids, it symbolizes balance, symmetry, and stability.

Formulas

The formulas for calculating a cube’s volume and surface area are simple, thanks to its regular structure.

• Volume
  The volume is calculated by cubing the length of an edge: $$ V = l^3 $$
• Total Surface Area
  The total surface area is the sum of the areas of its six faces: $$ A = 6l² $$
• Area of One Face
  The area of each face of a cube is equivalent to that of a square with a side equal to the edge length (l) of the cube: $$ A_B = l^2 $$

  Note. From this, the formula for the total surface area is derived. Since the cube has six faces, each with the same area (A_B=l²), we conclude that the total area of the cube is A=6A_B=6l².

• Diagonal
  The diagonal of the cube is found by multiplying the length of an edge by the square root of three: $$ d = l \cdot \sqrt{3} $$

So, given the length of an edge (l), you can easily calculate the cube's volume, total surface area, and the area of each individual face.

The Symmetry of the Cube

Thanks to its shape, the cube has several lines of symmetry, and it maintains its form regardless of the axis around which it is rotated.

The axes of symmetry are:

• The three lines connecting the centers of opposite faces, which serve as axes of rotation.
  
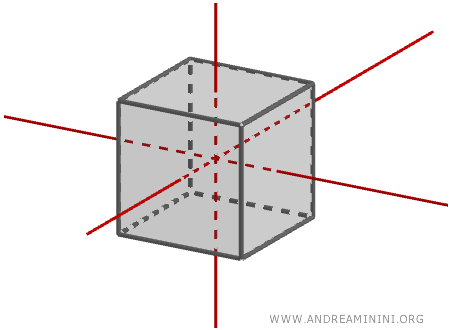
• The six lines connecting the midpoints of opposite edges, which are axes of symmetry.
  
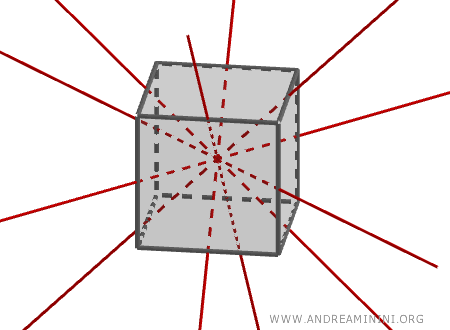
• The four diagonals connecting one vertex to the opposite vertex on the opposite face, which are axes of symmetry.
  

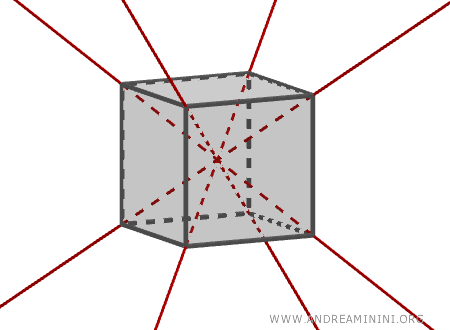
The cube’s diagonals intersect at a single point, known as the center of symmetry of the cube, which is also the center of a circumscribed sphere that passes through all the cube's vertices.

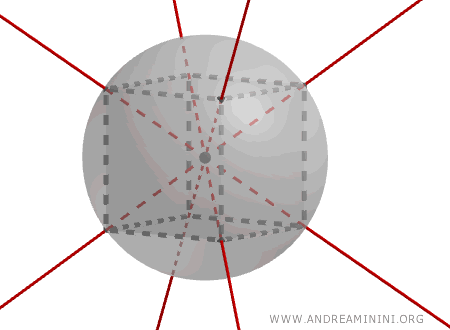
This makes the cube an important object of study in mathematics, particularly in group theory.

Additional Notes

Some additional insights about the cube:

• The cube is the only parallelepiped where all three dimensions are equal.
• Among all rectangular parallelepipeds with the same total surface area, the cube has the maximum volume.
• In mathematics, "cube" refers to raising a number to the third power
  This comes from the formula for the volume of a cube, which involves raising the edge length (l) to the power of three: $$ V = l^3  $$ This is why "cubing" a number means raising it to the third power.
• All of its faces are not only identical in shape but also in size, with each being a mirror image of the others.

And so on.