Sphere

A sphere is a solid formed by rotating a semicircle 360 degrees around its diameter. It’s a perfectly symmetrical geometric shape.

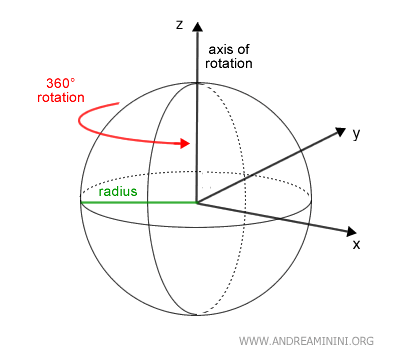
The complete rotation of the semicircle creates the spherical surface.

Point C is the center of the sphere and is equidistant from every point on the sphere’s surface.

The radius of the semicircle becomes the radius of the sphere, which is the distance from the center to any point on the surface.

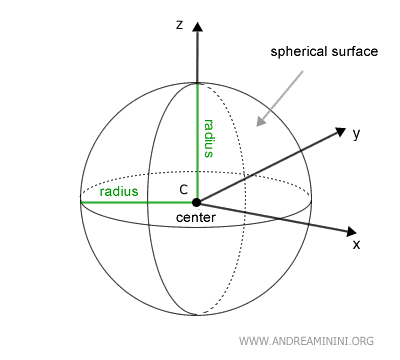
Similarly, you can think of a sphere as a solid of revolution formed by rotating a circle 180 degrees. The result is the same.

A sphere can also be defined as the set of all points in space (a geometric locus) that are at a distance less than or equal to a given point called the center (C).

A spherical surface, by contrast, is defined as the set of all points in space that lie at a distance from the center equal to the radius of the sphere.

The study of spheres dates back to ancient times. Greek mathematicians like Plato and Archimedes were among the first to explore their properties. Notably, Archimedes discovered key formulas for calculating the volume and surface area of spheres. Spheres have also held significant roles in philosophy and cosmology. To Greek philosophers, the sphere symbolized perfection, harmony, and the universe. This symbolism is also found in other cultures, where the sphere is often associated with concepts of completeness and infinity.

Formulas

Here are the key formulas for calculating a sphere's properties:

• Surface Area
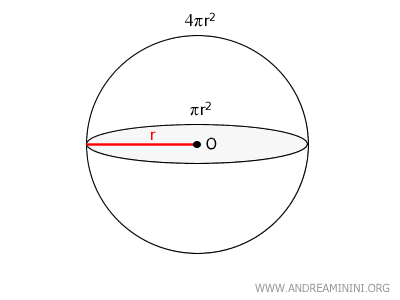
  The surface area of a sphere is given by the formula $$ 4πr^2 $$ where r is the radius of the sphere.

  Note. The surface area of a sphere is four times the area of its largest cross-sectional circle. $$ 4 \cdot \pi r^2 $$
  
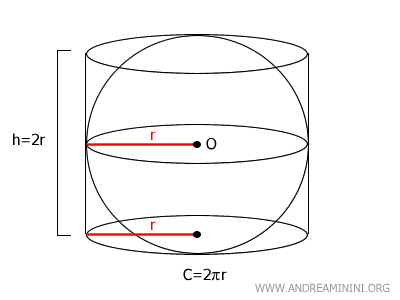
  It can also be shown that the surface area of a sphere is equal to the lateral surface area $ A_L $ of the cylinder that just contains it. $$ A_L = C \cdot h = 2 \pi r \cdot 2r = 4 \pi r^2 $$
  

• Volume
  The volume of a sphere is proportional to the cube of its radius, given by the formula: $$ \frac{4}{3}πr^3$$

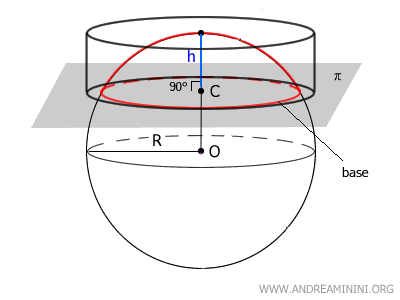
Spherical Caps

A spherical cap is the portion of a sphere’s surface bounded by a secant plane that cuts through the sphere.

When a plane (π) intersects a sphere, it divides its surface into two distinct regions. Each of these regions is called a cap or spherical cap.

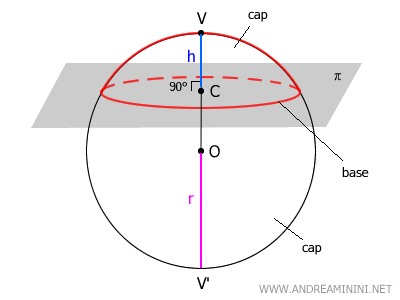
Each cap is defined by three key elements:

• The base: the circular cross-section created by the intersection of the plane and the sphere. This circle is centered at point C.
• The vertex (V): the point on the sphere that lies farthest from the plane, aligned with the center of the base along the sphere’s diameter.
• The height (h): the perpendicular distance from the vertex (V) to the center (C) of the base.

The diameter VV′ that passes through the base’s center (C) also serves as the axis of symmetry for the cap. This vertical axis bisects the cap into two mirror-image halves.

Special Cases

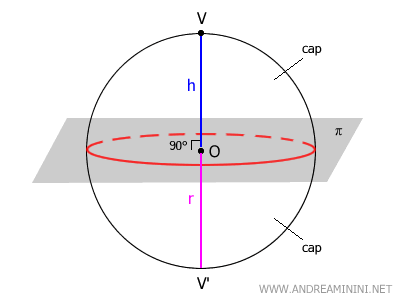
If the plane (π) passes through the center (O) of the sphere, the resulting caps are congruent hemispheres.

In this particular case, each cap comprises exactly half the surface area of the sphere, rather than just a curved segment.

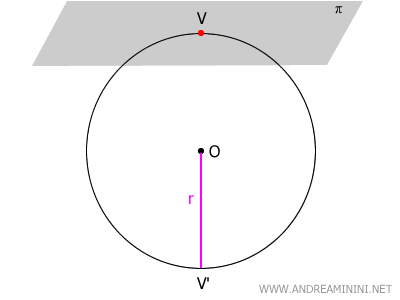
If the plane (π) is tangent to the sphere, the cap degenerates into a single point V on the sphere’s surface.

Note. A spherical cap preserves many of the sphere’s geometric properties - for instance, its curvature and symmetry - while being defined by a distinct base and vertex.

Surface Area of a Spherical Cap

The surface area of a spherical cap can be calculated using the formula

$$ A= 2 \pi R h $$

where $ R $ is the radius of the sphere and $ h $ is the height of the cap.

Example

Consider a sphere with a radius of \( R = 5\,cm \). If we slice the sphere exactly in half, the resulting cap has a height of $ h = R = 5\,cm $.

Applying the formula, we find the surface area of the cap:

\[ A = 2 \pi R h = 2 \pi \cdot 5 \cdot 5 = 50 \pi \approx 157.08\,cm^2 \]

This is precisely half the total surface area of the sphere.

Proof. The total surface area of a sphere is given by: \[ A_{\text{total}} = 4 \pi R^2 \] This formula represents the entire surface area of a sphere of radius \( R \). If we cut the sphere through its center, we obtain a hemisphere, whose surface area is exactly half that of the full sphere: \[ A_{\text{hemisphere}} = 2 \pi R^2 \] Now, let's examine a special case: a spherical cap whose height \( h \) is exactly equal to the radius \( R \) of the sphere. In other words, the cap covers an entire hemisphere. Substituting \( h = R \) into the general formula for the surface area of a cap or zone, we get: \[ S = 2 \pi R h \] which, with \( h = R \), becomes: \[ S = 2 \pi R \cdot R = 2 \pi R^2 \] matching exactly the surface area of the hemisphere as derived earlier. This confirms that the formula \( S = 2 \pi R h \) remains valid even in limiting cases, such as a hemispherical cap.

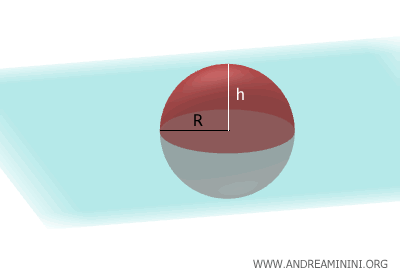
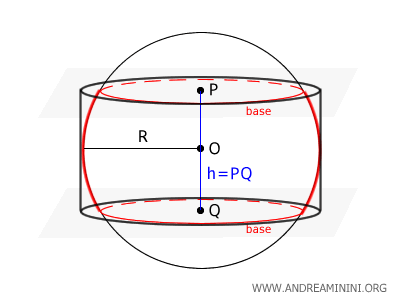
Thus, the surface area of a spherical zone is equivalent to the lateral surface area of a cylinder with the same radius as the sphere and a height equal to that of the cap. The lateral surface area of a cylinder is likewise given by $ S_L = 2 \pi R h $

Spherical Zone

A spherical zone is the portion of a sphere's surface bounded between two parallel planes cutting through the sphere.

These planes intersect the sphere in two circles, known as the bases of the zone, dividing the sphere’s surface into three distinct regions.

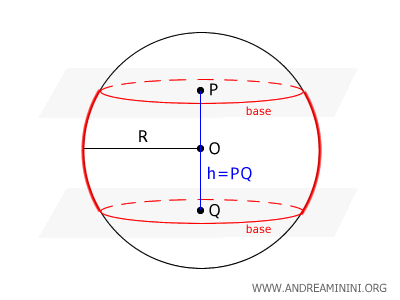
The region lying between the two planes is called a spherical zone. It forms a curved, belt-like strip between two circular cuts across the sphere.

Note. To visualize it, imagine the sphere as a globe: drawing two different lines of latitude creates a ring-shaped area between them - that’s the spherical zone.

The diameter of the sphere passing through the line segment $ PQ $, which connects the centers $ P $ and $ Q $ of the two bases, is known as the axis of symmetry of the zone. The distance between the two centers is called the height of the zone and is denoted by \( h \).

Surface Area of a Spherical Zone

The surface area \( S \) of a spherical zone is found using the same formula as for a spherical cap:

\[ S = 2 \pi R h \]

where \( R \) is the radius of the sphere and \( h \) is the distance between the two planes.

Note. A spherical cap is simply a special case of a spherical zone, where one of the bounding planes is tangent to the sphere’s surface. Therefore, the same formula applies: in both cases, the surface area depends solely on the radius of the sphere and the height of the curved section.

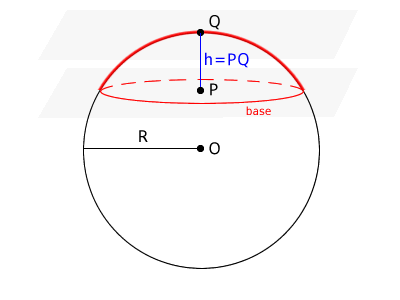
Example

Suppose we have a sphere with a radius of \( R = 10\,cm \) and two parallel planes cutting through it, creating a spherical zone with a height of \( h = 4\,cm \).

The surface area of the spherical zone is approximately \( 251.33\,cm^2 \)

$$ S = 2 \pi R h = 2 \pi \cdot 10 \cdot 4 = 80 \pi \approx 251.33\,cm^2 $$

Note. The surface area of the spherical zone can also be compared to the lateral surface area of a cylinder with the same radius as the sphere and a height equal to that of the zone. The lateral surface area of a cylinder is likewise given by $ S_L = 2 \pi R h $

Spherical Lune

A spherical lune is a section of a sphere’s surface bounded by two half-planes passing through the sphere’s center.

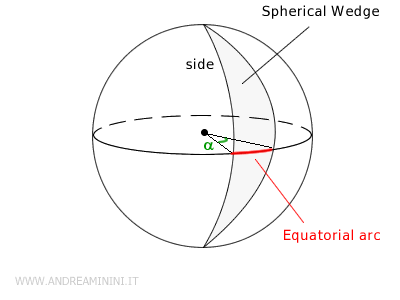
The key components of a spherical lune are:

• Dihedral angle: the solid angle (α) formed by the two half-planes.
• Equatorial arc: the arc of a great circle (analogous to the Earth's equator) contained within the lune.
• Lune sides: the semicircular arcs where the two half-planes intersect the sphere’s surface.

In simpler terms, a spherical lune looks much like an orange slice, cut along its natural segments.

Surface Area of a Spherical Lune

The surface area of a spherical lune depends on the measure of its dihedral angle. It can be calculated in two ways:

• If the dihedral angle is measured in radians: \[ S_f = 2 \alpha_{\text{rad}} R^2 \]
• If the dihedral angle is measured in degrees: \[ S_f = \frac{\alpha^\circ}{90^\circ} \pi R^2 \]

Here, \( S_f \) represents the area of the lune, \( R \) is the radius of the sphere, \( \alpha_{\text{rad}} \) is the dihedral angle in radians, and \( \alpha^\circ \) is the angle in degrees.

It’s important to note that the lune’s area is directly proportional to the size of the dihedral angle (α) relative to the sphere’s entire surface area.

Proof. The total surface area of a sphere is given by: \[ A_{\text{total}} = 4\pi R^2 \] A spherical lune represents a fraction of this area, proportional to its dihedral angle. When the angle is measured in radians, the proportion is between \( \alpha_{\text{rad}} \) and \( 2\pi \) (the measure of a full circle in radians): \[ A_{\text{lune}} = 4\pi R^2 \cdot \frac{ \alpha_{\text{rad}} }{2 \pi} =2\alpha_{\text{rad}} R^2 \] When measured in degrees, the proportion is between \( \alpha^\circ \) and \( 360^\circ \): \[ A_{\text{lune}} = 4\pi R^2 \cdot \frac{ \alpha^\circ }{360^\circ} = \frac{\alpha^\circ}{90^\circ} \pi R^2 \]

Example

Let's find the surface area of a spherical lune cut from a sphere with a radius of \( R = 5 \, \text{cm} \), and a dihedral angle of \( 60^\circ \). Applying the formula:

\[ S_f = \frac{60^\circ}{90^\circ} \pi R^2 = \frac{2}{3} \pi (5)^2 \]

\[ S_f = \frac{2}{3} \pi \times 25 = \frac{50}{3} \pi \, \text{cm}^2 \]

Thus, the lune’s surface area is approximately \( 52.36 \, \text{cm}^2 \).

Example 2

Consider a sphere with a radius of \( 10 \, \text{cm} \), and a lune with a dihedral angle of \( \frac{\pi}{4} \, \text{radians} \). We calculate the surface area using the formula for radians:

\[ S_f = 2 \alpha_{\text{rad}} R^2 = 2 \times \frac{\pi}{4} \times 10^2 \]

\[ S_f = \frac{\pi}{2} \times 100 = 50\pi \, \text{cm}^2 \]

Therefore, the surface area of the lune is approximately \( 157.08 \, \text{cm}^2 \).

Spherical Segment

A spherical segment is a portion of a solid obtained by slicing a sphere with one or two parallel planes.

A] Spherical Segment with One Base

A spherical segment with one base is formed by cutting a sphere with a single plane and removing either the portion above or below the plane.

The lower (or upper) surface of the segment is a spherical cap, also known as a "hemispherical cap" when the plane divides the sphere exactly in half.

The base of the segment is the circular cross-section where the plane intersects the sphere.

Volume Formula

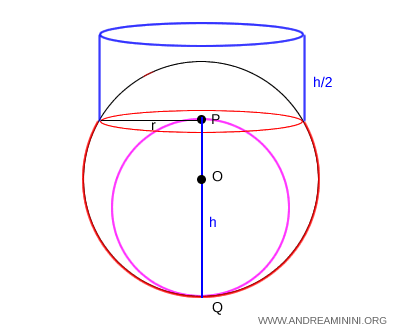
If the spherical segment has a height of $ h $ and its base has a radius of $ r $, its volume is equivalent to the combined volume of a sphere with diameter $ h $ and a cylinder that shares the same base as the segment and has a height of $ h/2 $.

$$ V = \frac{4}{3} \pi \left( \frac{h}{2} \right)^3 + \pi r^3 \cdot \frac{h}{2} $$

This formula is simply the sum of the volumes of a sphere and a cylinder.

You can use this formula to compute the volume of either the upper portion of a one-base spherical segment, as shown in the example above, or the lower portion.

The Compact Form of the Volume Formula

The volume formula can also be written in a more compact form:

$$ V = \frac{1}{3} \pi h^2 (3R-h) $$

where $ R $ is the radius of the sphere.

Proof. Consider a spherical segment with one base, of height $ h = CV $ and base radius $ r = BC $.

Applying Euclid’s second theorem to the right triangle VAB, we obtain the relation: $$ BC^2 = AC \cdot CV $$ where $ BC $ is the radius $ r $ of the base of the spherical segment. $$ r^2 = AC \cdot CV $$ The segment $ AC = 2R - h $ represents the difference between the sphere’s diameter and the height of the spherical segment. $$ r^2 = (2R - h) \cdot CV $$ Since $ CV $ is simply the height $ h $ of the segment, we have: $$ r^2 = (2R - h) \cdot h $$ $$ r^2 = 2Rh - h^2 $$ Now, substituting this expression for $ r^2 $ into the volume formula for the spherical segment: $$ V = \frac{4}{3} \pi \left( \frac{h}{2} \right)^3 + \pi r^2 \cdot \frac{h}{2} $$ $$ V = \frac{4}{3} \pi \left( \frac{h}{2} \right)^3 + \pi (2Rh - h^2) \cdot \frac{h}{2} $$ $$ V = \frac{4}{3} \pi \left( \frac{h}{2} \right)^3 + \pi R h^2 - \frac{\pi h^3}{2} $$ Simplifying the first term: $$ V = \frac{4}{3} \pi \cdot \frac{h^3}{8} + \pi R h^2 - \frac{\pi h^3}{2} $$ $$ \begin{aligned} V &= \frac{\pi h^3}{6} + \pi R h^2 - \frac{\pi h^3}{2} \\[2pt] &= \pi R h^2 + \left( \frac{1}{6} - \frac{1}{2} \right) \pi h^3 \\[2pt] &= \pi R h^2 - \frac{\pi h^3}{3} \end{aligned} $$ Factoring the expression gives: $$ \boxed{ V = \frac{1}{3} \pi h^2 (3R - h) } $$ which is the compact form of the volume formula for a spherical segment with one base.

B] Spherical Segment with Two Bases

A spherical segment is a portion of a sphere enclosed between two parallel planes that slice through it.

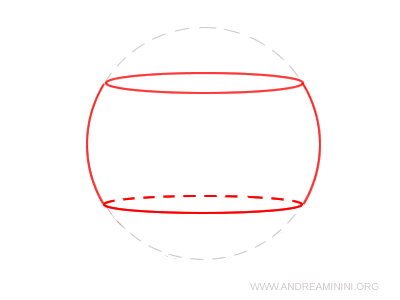
Put simply, it is a solid obtained by cutting a sphere with two horizontal planes: the section of the sphere that remains between the two planes is called a spherical segment.

The final shape resembles a kind of curved cylinder.

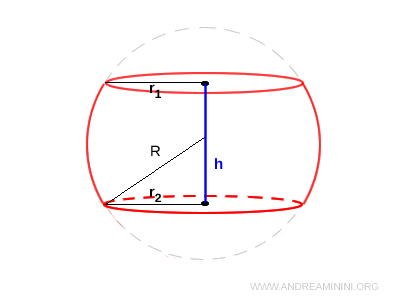
The main components of a spherical segment are:

• The upper and lower bases, which are circular cross-sections of the sphere where it intersects the planes.
• The curved lateral surface, known as the spherical zone.
• The height of the segment, denoted by $ h $, which is the vertical distance between the two planes.
• The radius of the sphere, which is the radius of the original sphere from which the segment is derived.

Note. The spherical segment should not be confused with a spherical cap, which is the portion of a sphere above (or below) a single cutting plane. Nor is it the same as a spherical wedge, which is a portion of the spherical surface bounded by two half-planes passing through the center of the sphere.

Volume Formula

If the spherical segment has a height $ h $, base radii $ r_1 $ and $ r_2 $, and the sphere itself has radius $ R $, its volume is given by:

$$ V = \frac{πh}{6} (3r_1^2 + 3r_2^2 + h^2) $$

Note. The volume of a spherical segment with two bases can be interpreted as the sum of the volumes of two cylinders - each having height $ h/2 $ and bases matching those of the segment - plus the volume of a sphere whose diameter equals the height of the segment.

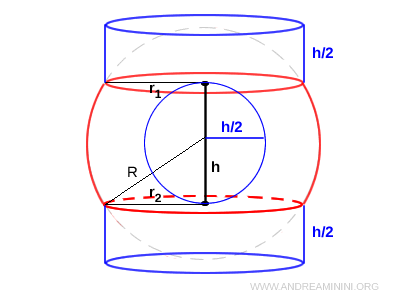
For example, the volumes of the two cylinders are: $$ V_1 = \pi r_1^2 \cdot \frac{h}{2} $$ $$ V_2 = \pi r_2^2 \cdot \frac{h}{2} $$ The volume of a sphere with diameter $ h $ (and radius $ h/2 $) is: $$ V_3 = \frac{4}{3} \pi \left( \frac{h}{2} \right)^3 $$ Adding the three volumes: $$ V = V_1 + V_2 + V_3 $$ $$ V = \pi r_1^2 \cdot \frac{h}{2} + \pi r_2^2 \cdot \frac{h}{2} + \frac{4}{3} \pi \left( \frac{h}{2} \right)^3 $$ $$ V = \pi r_1^2 \cdot \frac{h}{2} + \pi r_2^2 \cdot \frac{h}{2} + \frac{4}{3} \pi \, \frac{h^3}{8} $$ $$ V = \pi r_1^2 \cdot \frac{h}{2} + \pi r_2^2 \cdot \frac{h}{2} + \frac{1}{6} \pi h^3 $$ $$ V = \frac{1}{6} \pi h \left( 3r_1^2 + 3r_2^2 + h^2 \right) $$ This is the final formula for the volume of a spherical segment.

Spherical Wedge

A spherical wedge is the portion of a sphere bounded by two distinct semicircular planes, which form the "faces" of the wedge. The curved surface that connects these faces is a spherical lune, sometimes referred to as the "lateral surface."

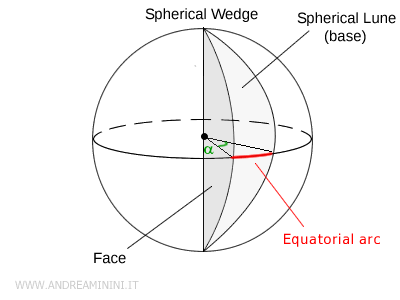
The shape of this solid closely resembles a slice of an orange.

The volume of a spherical wedge is directly proportional to the angle between its two faces.

When the angle is measured in radians:

$$V : \frac{4}{3} \pi R^3 = \alpha_{rad} : 2\pi$$

This yields the following formula for the volume of a spherical wedge:

$$V = \alpha_{rad} \cdot \frac{2}{3} R^3$$

Note. If the angle is measured in degrees, the proportion becomes: $$V : \frac{4}{3} \pi R^3 = \alpha : 360^\circ$$ The corresponding volume formula is: $$V = \frac{\alpha}{360^\circ} \cdot \frac{4}{3} \pi R^3$$ or equivalently: $$V = \frac{\alpha}{270^\circ} \pi R^3$$

Spherical Ring

A spherical ring is a solid formed by subtracting an inscribed frustum of a cone from a spherical segment with two bases.

It is constructed by taking a spherical segment with two circular bases and inscribing a frustum of a cone whose lateral surface aligns precisely with the spherical segment’s inner surface.

The two circular sections define the bases of the segment.

Inside this spherical segment, we can inscribe a frustum of a cone - that is, the portion of a cone lying between two planes parallel to its base.

The bases of the truncated cone coincide exactly with the circular bases of the spherical segment.

The region of the sphere lying between the lateral surface of the truncated cone and the corresponding portion of the spherical segment forms the spherical ring.

In other words, the spherical ring is what remains of the spherical segment after the volume occupied by the truncated cone has been “carved out.”

Volume of the Spherical Ring

The volume of the spherical ring is simply the difference between the volume of the spherical segment and that of the inscribed frustum of a cone.

$$ V = \frac{1}{6} \pi a^2 h $$

where $ a $ is the slant height (or apothem) of the truncated cone, and $ h $ is its height.

Proof. We begin by expressing the volume of the spherical ring as the difference between the volumes of the spherical segment and the frustum of a cone: $$ V_{\text{ring}} = V_{\text{spherical segment}} - V_{\text{truncated cone}} $$ The volume of a spherical segment of height $h$ with base radii $r_1$ and $r_2$ is given by: $$ V_{\text{spherical segment}} = \frac{\pi h}{6} \left( 3r_1^2 + 3r_2^2 + h^2 \right) $$ The volume of a frustum of a cone of height $h$, with base radii $r_1$ and $r_2$, is: $$ V_{\text{truncated cone}} = \frac{1}{3} \pi h \left( r_1^2 + r_1 r_2 + r_2^2 \right) $$ We now compute their difference: $$ V_{\text{ring}} = V_{\text{spherical segment}} - V_{\text{truncated cone}} $$ $$ V_{\text{ring}} = \frac{\pi h}{6} \left( 3r_1^2 + 3r_2^2 + h^2 \right) - \frac{1}{3} \pi h \left( r_1^2 + r_1 r_2 + r_2^2 \right) $$ Bringing the terms under a common denominator: $$ V_{\text{ring}} = \frac{\pi h}{6} \left[ (3r_1^2 + 3r_2^2 + h^2) - 2 ( r_1^2 + r_1 r_2 + r_2^2 ) \right]
$$ Expanding the terms inside the brackets: $$ V_{\text{ring}} = \frac{\pi h}{6} \left[ 3r_1^2 + 3r_2^2 + h^2 - 2r_1^2 - 2r_1 r_2 - 2r_2^2 \right] $$ $$ V_{\text{ring}} = \frac{\pi h}{6} \left[ r_1^2 + r_2^2 + h^2 - 2 r_1 r_2 \right] $$ Notice that the expression $ r_1^2 + r_2^2 - 2r_1 r_2 $ is equivalent to the square of a binomial: $ (r_1 - r_2)^2 $. Thus, we can rewrite: $$ V_{\text{ring}} = \frac{\pi h}{6} \left[ (r_1 - r_2)^2 + h^2 \right] $$ Now, introducing the slant height $a$ of the truncated cone, we know geometrically that $ a^2 = (r_1 - r_2)^2 + h^2 $. This leads us to the final compact expression: $$ V_{\text{ring}} = \frac{1}{6} \pi a^2 h $$ where $a$ is the slant height of the inscribed truncated cone, and $h$ is the height of the spherical segment.

Spherical Sector

A spherical sector is a portion of a sphere bounded by a cone whose vertex coincides with the center of the sphere and whose base is a spherical cap.

In other words, a spherical sector is the solid obtained by rotating a circular sector through 360° about an axis that does not pass through it.

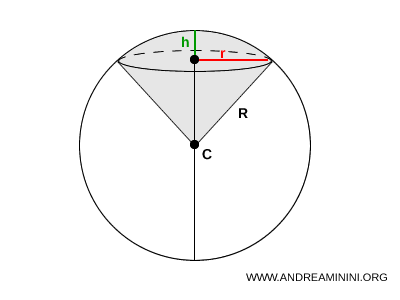
It can be regarded as a composite solid consisting of a spherical segment with one base and a right circular cone sharing the same base, with its vertex at the center of the sphere.

However, this represents only a particular instance of a spherical sector.

The volume of a spherical sector is given by:

$$ V = \frac{2}{3} \pi R^2 h $$

where $ R $ is the radius of the sphere and $ h $ is the height of the spherical segment.

The surface area is:

$$ A = \pi R (2h + r) $$

where $ r $ is the radius of the circular sector.

Proof. By decomposing the spherical sector into a spherical segment and a cone with its vertex at the center of the sphere, and applying the relationships between the geometric parameters, we can derive the classical formula for the volume of a spherical sector. The volume of the spherical segment is: $$ V_{\text{seg}} = \frac{1}{3} \pi h^2 (3R - h) $$ The volume of the cone is: $$ V_{\text{cone}} = \frac{1}{3} \pi r^2 (R - h) $$ From the right triangle formed by slicing the sphere with the base plane, we obtain the following relation between $ r $, $ h $, and $ R $: $$ r^2 = R^2 - (R - h)^2 = 2Rh - h^2 $$ For a detailed explanation of this step, refer to the proof I previously provided for the compact formula for the volume of a spherical segment. The volume of the spherical sector is then obtained by summing the volumes of the spherical segment and the cone: $$ \begin{aligned} V_{\text{sector}} &= V_{\text{seg}} + V_{\text{cone}} \\[2pt] &= \frac{1}{3} \pi \left[ h^2 (3R - h) + r^2 (R - h) \right]. \end{aligned} $$ Substituting $ r^2 = 2Rh - h^2 $ yields: $$ \begin{aligned} h^2 (3R - h) &+ (2Rh - h^2)(R - h) \\[2pt] &=\; 3Rh^2 - h^3 + 2R^2 h - 3Rh^2 + h^3 \\[2pt] &= 2R^2 h \end{aligned} $$ Therefore, the volume of the spherical sector simplifies to: $$ \boxed{\, V_{\text{sector}} = \frac{1}{3} \pi (2R^2 h) = \frac{2}{3} \pi R^2 h \,} $$ In short, combining the contributions of the spherical segment and the cone leads directly to the standard formula for the volume of a spherical sector.

These formulas apply exclusively to a standard spherical sector - that is, the portion of a sphere bounded by a right circular cone whose vertex lies at the center of the sphere.

In more complex configurations (such as oblique sectors, spherical shells, or combinations of multiple solids), calculating the volume requires a detailed analysis of the sector’s specific geometry.

Other configurations of spherical sectors

Depending on the configuration, the volume of a spherical sector can be expressed as either the sum or the difference of the volumes of other solids.

For example, in this case, the volume of the spherical sector is calculated by subtracting the combined volume of two cones from the volume of a spherical segment.

In another case, the volume of the spherical sector is obtained by taking the difference between the volumes of two spherical sectors.

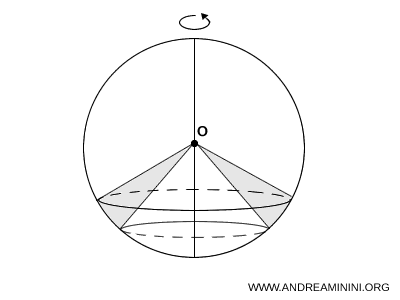
Therefore, the appropriate volume formula must be determined according to the specific geometric configuration.

Sphere in Analytic Geometry

In analytic geometry, a sphere is represented by an equation that defines all points in space at a constant distance from a fixed point, the center.

The standard equation of a sphere with its center at (x₀,y₀,z₀) and radius r is:

$$ (x−x_0)^2+(y−y_0)^2+(z−z_0)^2=r^2 $$

Where (x,y,z) are the coordinates of any point in space.

This equation is a three-dimensional extension of the circle equation in the Cartesian plane.

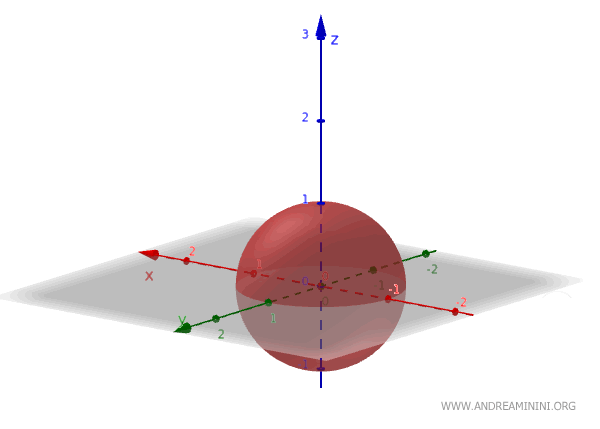
If the sphere is centered at the origin O(0,0,0), the equation simplifies to:

$$ x^2 + y^2 + z^2 = r^2 $$

Here’s an example of a sphere centered at the origin of the Cartesian plane with a unit radius.

The equation of a sphere can also be expressed in polar coordinates:

$$ \begin{cases} x = x_0 + r \sin \theta \cos \theta \\ \\ y = y_0 + r \sin \theta \sin \theta \\ \\ z = z_0 + r \cos \theta \end{cases} $$

Additional Notes

Here are a few more details about spheres:

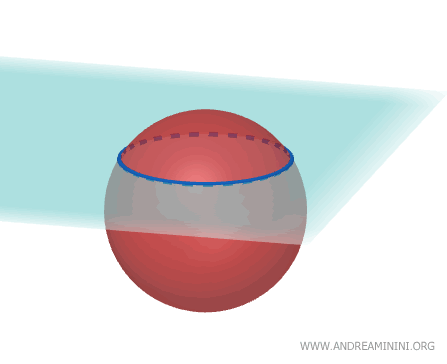
• Sections
  Any intersection between a plane and a sphere forms a circle. If the plane passes through the center, the circle is at its largest.
  
• Chord
  A chord of a sphere is a line segment connecting any two distinct points on the surface.
• Diameter
  The diameter of a sphere is twice the radius. It’s a chord that passes through the center of the sphere. $$ d = 2r $$
• External, Tangent, and Secant Planes
  A plane α in relation to a sphere Σ with center C and radius r can be:
  • External if the distance between plane α and sphere Σ is greater than the radius r. The plane and the sphere do not intersect.
  • Tangent if the distance between plane α and sphere Σ is equal to the radius r.
  • Secant if the distance between plane α and sphere Σ is less than the radius r.
• Hypersphere (or n-Sphere)
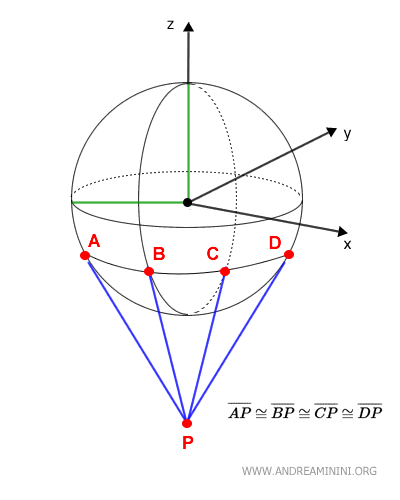
  A generalization of the sphere to higher dimensions. A 4-sphere is the four-dimensional analogue of an ordinary sphere.
• Theorem of Tangent Segments to a Sphere from an External Point
  Tangent segments to a sphere drawn from an external point P are congruent: $ \overline{AP} \cong \overline{BP} \cong \overline{CP} \cong \overline{DP} $. All tangent segments to the sphere from the same point P form a cone with a circular base.
  

And so on.