Euclid's Second Theorem

In a right triangle, the square constructed on the altitude to the hypotenuse has the same area as the rectangle formed by the projections of the legs onto the hypotenuse.

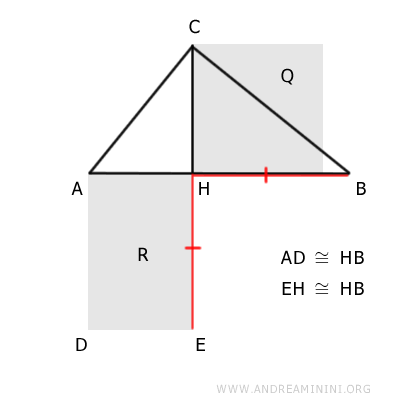
In other words, consider a square Q with one side equal to the altitude CH of the right triangle relative to the hypotenuse AB.

The projections of the legs onto the hypotenuse divide it into two segments, AH and BH. Therefore, we construct a rectangle R using these two segments.

The square Q and the rectangle R are equivalent polygons, meaning they have the same area.

Corollary

As a corollary, in a right triangle, the altitude relative to the hypotenuse is the geometric mean of the projections of the legs onto the hypotenuse.

Thus, in a proportion, one projection (p₁) is to the altitude (h) as the altitude is to the other projection (p₂) of the leg on the hypotenuse.

Note: The proportion p₁:h=h:p₂ is equivalent to Euclid's second theorem $$ p_1 : h = h : p_2 \rightarrow h^2 = p_1 \cdot p_2 $$ which states that the area of the square constructed on the altitude is equal to the area of the rectangle formed by the projections of the legs onto the hypotenuse.

Inverse Theorem

If in a triangle, the square of the altitude is equal to the product of the lengths of the two segments into which the altitude divides the opposite side, then the triangle is a right triangle. $$ \overline{CH}^2 = \overline{AH} \cdot \overline{BH} $$

In this case, the vertex (C) from which the altitude originates forms a right angle (90°).

An Example

Consider this right triangle ABC:

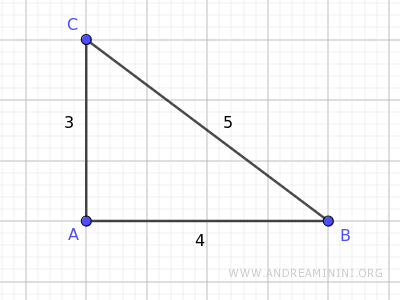
The right triangle has legs AB = 4 and AC = 3, with the hypotenuse BC = 5.

Draw the altitude of the triangle relative to the hypotenuse.

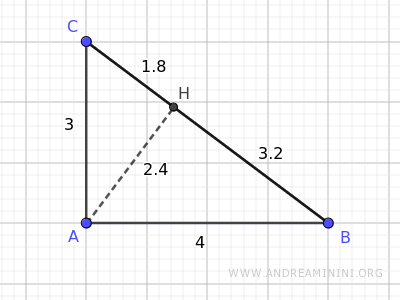
The altitude AH of the triangle measures 2.4 and divides the hypotenuse into two segments of lengths 1.8 and 3.2.

The square of the altitude has an area of 5.76.

$$ \overline{AH}^2 = 2.4^2 = 5.76 $$

The area of a rectangle with one side 1.8 and the other side 3.2 is also 5.76.

$$ \overline{BH} \cdot \overline{CH} = 3.2 \cdot 1.8 = 5.76 $$

Therefore, the square and the rectangle have the same area, meaning they are equivalent polygons.

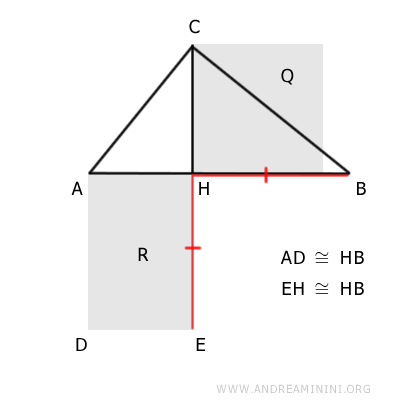
The Proof

Consider a right triangle ABC.

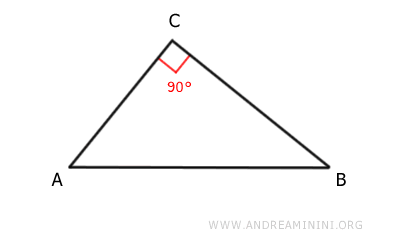
The legs of the right triangle are segments AC and BC.

The segment CH is the altitude of the triangle relative to the hypotenuse AB.

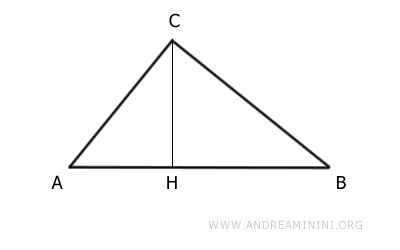
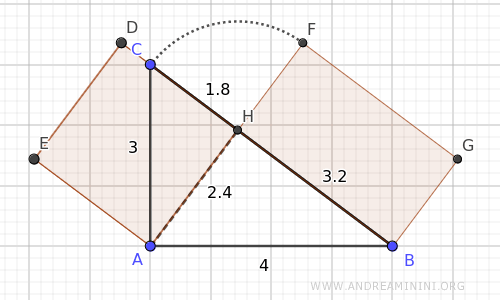
Construct a square Q1 on the altitude CH.

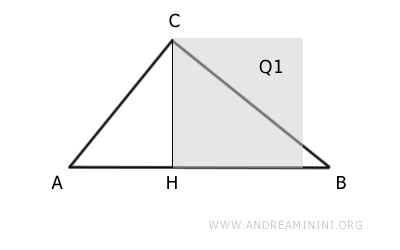
Point H is also the projection of the legs that divides the hypotenuse into two segments AH and BH.

$$ \overline{AB} = \overline{AH} + \overline{BH} $$

Construct a rectangle R1 on segment AH with lateral sides congruent to AD≅EH≅AB with the hypotenuse AB.

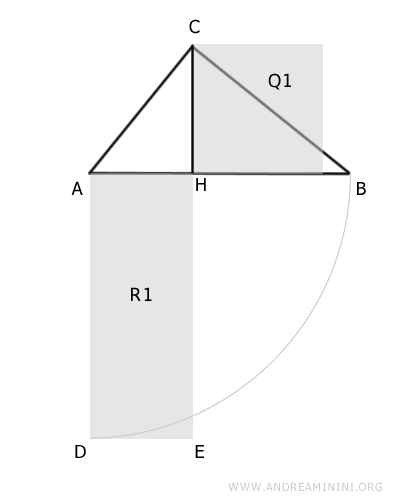
We can consider rectangle R1 as a polygon composed of a square Q2 with a side congruent to AH and a rectangle R2.

$$ R1 \doteq Q2 + R2 $$

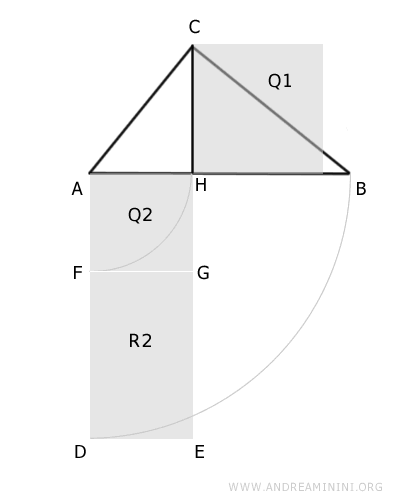
It is important to note that rectangle R2 has sides equal to the projections of the legs of triangle ABC on the hypotenuse i.e., AH≅FG≅DE and BH≅FD≅EG.

$$ AH \cong FG \cong DE $$

$$ BH \cong FD \cong EG $$

Therefore, we need to show that square Q1 and rectangle R2 are equivalent polygons, meaning they have the same area.

 

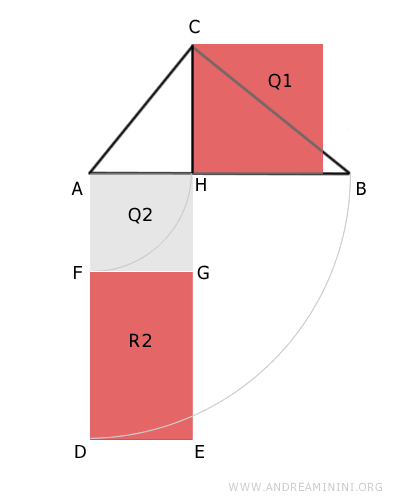
Now, focus on the right triangle AHC, which is a component within triangle ABC.

According to the Pythagorean theorem, the sum of the squares of the legs of triangle AHC is equal to the square on the hypotenuse AC.

$$ Q3 \doteq Q1 + Q2 $$

From this, we deduce that the area of square Q1 is equal to the difference between Q3 and Q2.

$$ Q1 \doteq Q3 - Q2 $$

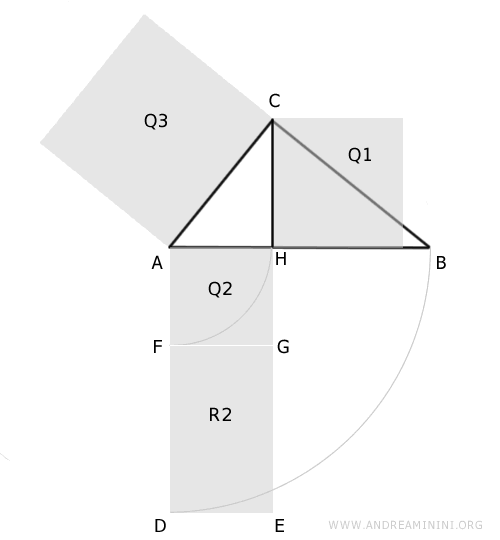
According to the first theorem of Euclid, area Q3 is equal to area R1=Q2+R2

$$ Q3 \doteq R1 $$

$$ Q3 \doteq Q2 + R2 $$

Thus, R2 is also equivalent to Q3-Q2

$$ R2 \doteq Q3 - Q2 $$

Consequently, both Q1 and R2 are equivalent to Q3-Q2.

$$ R2 \doteq Q3 - Q2 \dot Q1 $$

Therefore, by the transitive property, Q1 and R2 are equivalent, meaning they have the same area.

$$ R2 \doteq Q1 $$

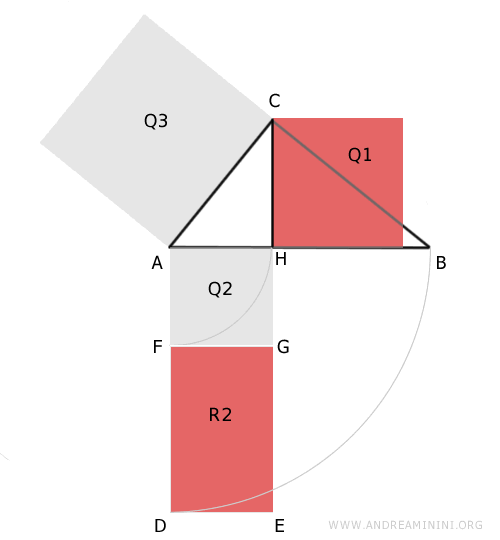
This demonstrates that the square Q1 constructed on the altitude CH relative to the hypotenuse AB of triangle ABC is equivalent to rectangle R2, which has sides equal to the projections AH≅FG and BH≅DF of the legs.

Corollary

In a right triangle, the altitude (h) relative to the hypotenuse is the geometric mean between the projections p₁ and p₂ of the legs onto the hypotenuse.

$$ p_1 : h = h : p_2  $$

In other words, the projection of the shorter leg (p₁) is to the altitude (h) as the altitude is to the projection of the longer leg (p₂).

This means that the square constructed on the altitude is equivalent, i.e., has the same area, as the rectangle constructed with one projection as the height of the other projection.

$$ \frac{p_1}{h} = \frac{h}{p_2} $$

$$ h^2 = p_1 \cdot p_2 $$

This brings us back to Euclid's second theorem.

Example

For an example, consider the right triangle ABC where all measurements are known.

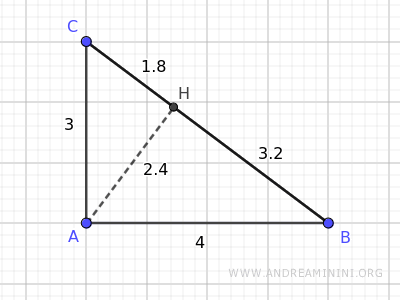
In this case, the length of the shorter leg (AC) is 3, the length of the longer leg (AB) is 4.

Finally, the altitude relative to the hypotenuse measures 2.4.

According to the corollary of Euclid's second theorem, the following proportion must hold:

$$ p_1 : h = h : p_2  $$

We already know that the altitude (h) relative to the hypotenuse measures 2.4.

$$ p_1 : 2.4 = 2.4 : p_2  $$

In this example, the projection of the shorter leg (p₁) onto the hypotenuse has a length of 1.8, while the projection of the longer leg (p₂) is 3.2.

$$ 1.8 : 2.4 = 2.4 : 3.2  $$

Transform the proportion into an equivalent fraction and perform the calculations:

$$ \frac{1.8}{2.4} = \frac{2.4}{3.2} $$

$$ 0.75 = 0.75 $$

The proportion is satisfied.

The Proof

Consider a right triangle ABC.

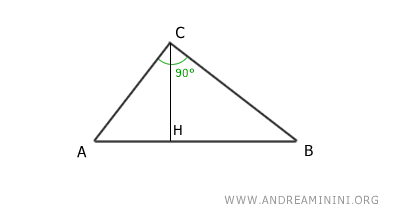
The altitude relative to the hypotenuse (CH) divides the right angle into two complementary angles, γ₁ and γ₂, whose sum is γ₁ + γ₂ = 90°.

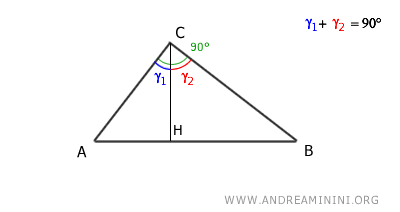
The altitude CH divides the triangle into two right triangles ACH and CBH.

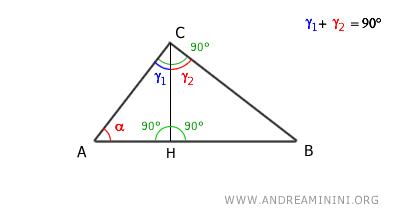
Knowing that the sum of the interior angles of a triangle is always equal to a straight angle (180°):

$$ \alpha + \gamma_1 + 90° = 180° $$

we deduce that in triangle ACH the angles α and γ₁ are complementary angles.

$$ \alpha + \gamma_1 = 180° - 90° $$

$$ \alpha + \gamma_1 = 90° $$

Since α + γ₁ = 90° and γ₁ + γ₂ = 90°, we deduce that the angles α and γ₂ are congruent angles α≅γ₂ because they are complementary to the same angle.

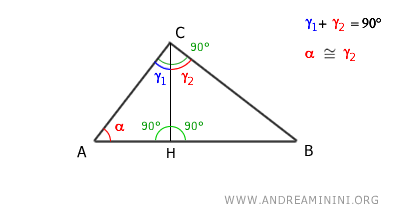
By the first criterion of similarity of triangles, the two triangles ACH and CBH are similar because they have two congruent angles: the right angle (90°) and the congruent acute angles α≅γ₂

$$ ACH \approx CBH $$

Since they are similar triangles, triangles ACH and CBH have corresponding sides in proportion.

$$ \overline{AC} : \overline{BC} = \overline{AH} : \overline{CH} = \overline{CH} : \overline{BH} $$

This proves the corollary of Euclid's second theorem.

$$ \overline{AH} : \overline{CH} = \overline{CH} : \overline{BH} $$

Where AH is the projection p₁ on the hypotenuse of the shorter leg, while BH is the projection p₂ of the longer leg on the hypotenuse.

$$ p_1 : \overline{CH} = \overline{CH} : p_2 $$

Finally, CH is the altitude of the right triangle ABC relative to the hypotenuse.

$$ p_1 : h = h : p_2 $$

And so on.