Right Triangle with 30° and 60° Angles
A right triangle with 30° and 60° angles is exactly half of an equilateral triangle.
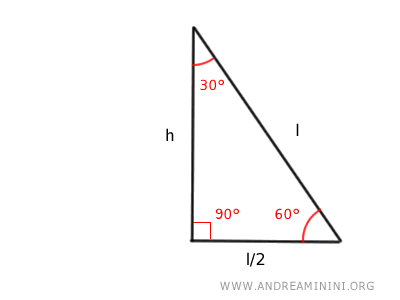
The height (h) and the side (l) of this right triangle can be calculated using these formulas: $$ l = \frac{2h}{\sqrt{3}} = \frac{2h }{3} \sqrt{3} $$ $$ h = \frac{l}{2} \sqrt{3} $$ The base (l/2) of the triangle is exactly half of the hypotenuse (l) opposite the right angle.
Explanation
If you rotate the right triangle around its longer leg, you get an equilateral triangle, which has three 60° angles and three equal sides.
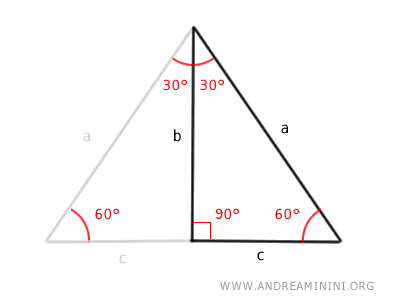
One important feature of the 30°, 60°, 90° right triangle is that knowing the length of one side allows you to determine the lengths of the other two sides.
$$ a = \frac{2b}{\sqrt{3}} = \frac{2b \sqrt{3}}{3} $$
$$ b = \frac{a}{2} \sqrt{3} $$
$$ c = \frac{a}{2} $$
This is possible because of the mathematical relationships between the sides and the Pythagorean theorem.
Note: These formulas apply only to triangles with internal angles of 30°, 60°, and 90°.
Proof
To prove the formulas for the 30°, 60°, 90° triangle, I use the Pythagorean theorem.
According to the Pythagorean theorem, in a right triangle, the square of the hypotenuse (a2) is equal to the sum of the squares of the legs (b2 + c2).
$$ a^2 = b^2 + c^2 $$
Knowing that the right triangle with 30° and 60° angles is half of an equilateral triangle, we deduce that the leg c = a/2 is half the hypotenuse, because in an equilateral triangle, all sides are equal (a = 2c).
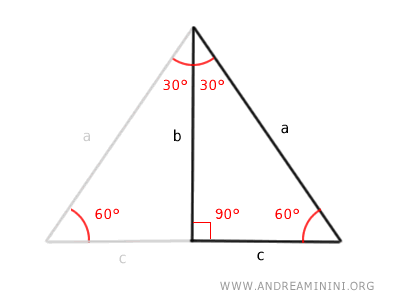
Thus, we can express the side c = a/2 as half the hypotenuse (a).
$$ a^2 = b^2 + ( \frac{a}{2}) ^2 $$
This relationship between the sides of the right triangle allows us to solve the triangle in various ways, depending on which side is known.
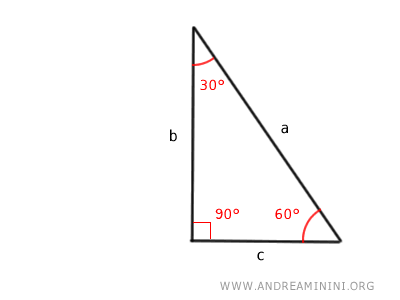
For example, if we know the hypotenuse (a), we can calculate the lengths of the other sides
$$ b^2 = a^2 - ( \frac{a}{2}) ^2 $$
$$ b^2 = a^2 - \frac{a^2}{4} $$
$$ b^2 = \frac{4a^2 - a^2}{4} $$
$$ b^2 = \frac{3a^2}{4} $$
$$ \sqrt{b^2} = \sqrt{ \frac{3a^2}{4} } $$
$$ b = \frac{a}{2} \sqrt{3} $$
The other leg (c) is simply calculated by dividing the hypotenuse by two
$$ c = \frac{a}{2} $$
If, on the other hand, we know the longer leg (b), we can calculate the hypotenuse (a) and the shorter leg (c = a/2).
$$ b^2 = a^2 - ( \frac{a}{2}) ^2 $$
$$ b^2 = a^2 - \frac{a^2}{4} $$
$$ b^2 = \frac{4a^2 - a^2}{4} $$
$$ b^2 = \frac{3a^2}{4} $$
$$ \frac{4b^2}{3} = a^2 $$
$$ \sqrt{ \frac{4b^2}{3} } = \sqrt{ a^2 } $$
$$ \frac{2b}{\sqrt{3}} = a $$
By multiplying both the numerator and the denominator of the fraction by √3, we use the property of invariance of fractions.
$$ \frac{2b}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = a $$
$$ \frac{2b \cdot \sqrt{3}}{\sqrt{3}} \ = a $$
$$ \frac{2b \sqrt{3}}{3} = a $$
Once the hypotenuse (a) is known, we get the shorter leg by noting that c = a/2
$$ c = \frac{a}{2} $$
And so forth.
