Circumscribed Circle's Radius Around a Triangle
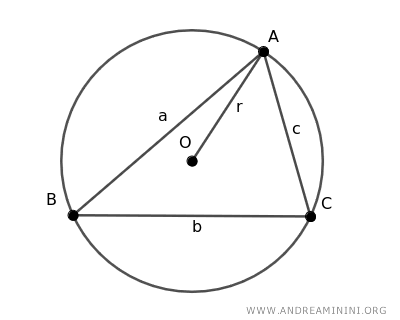
The radius of a circle that circumscribes a triangle is determined by the ratio of the product of the triangle's sides (a·b·c) to four times its area (A), expressed as $$ r = \frac{a \cdot b \cdot c}{4 \cdot A} $$ Here, a, b, and c represent the lengths of the triangle’s sides, and A signifies the triangle's area.
This equation is intrinsically linked to Heron's formula, which offers a method to calculate a triangle’s area using its semi-perimeter.
$$ A=p \cdot (p−a) \cdot (p−b) \cdot (p−c) $$
Where p stands for the semi-perimeter of the triangle, calculated as 2p=a+b+c.
Integrating Heron's formula for area A into the equation for R reveals a direct correlation between the triangle’s sides (a, b, c), its semi-perimeter (p), and the radius (r) of the encompassing circle.
$$ r = \frac{a \cdot b \cdot c}{4 \cdot A} = \frac{a \cdot b \cdot c}{4 \cdot p \cdot (p−a) \cdot (p−b) \cdot (p−c)} $$
Through geometric relationships involving the circumscribed circle and triangle properties, the radius r of the circumscribed circle can be related to the area A and the sides of the triangle. For further insight, refer to the demonstration below.
A Real-World Example
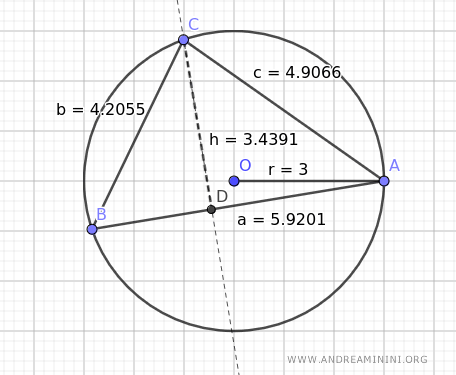
For illustration, let's examine a circle with a radius of OA=3, within which any triangle ABC is inscribed.
To test the formula's accuracy,
$$ r = \frac{a \cdot b \cdot c}{4 \cdot A} $$
Replacing the variables with the sides' lengths a=5.9201, b=4.9066, and c=4.2055,
$$ r = \frac{5.9201 \cdot 4.9066 \cdot 4.2055}{4 \cdot A} $$
$$ r = \frac{122.1586}{4 \cdot A} $$
The area of the triangle, calculated by the semi-product of its base and height, yields
$$ A = \frac{a \cdot h}{2} = \frac{5.9201 \cdot 3.4391}{2} = 10.1799 $$
Upon substituting the triangle's area A=10.1799 into the radius formula,
$$ r = \frac{122.1586}{4 \cdot 10.1799} \approx 3 $$
This computation confirms a circumscribed circle radius of r=3 around the triangle.
The outcome validates the initial radius measurement provided at the example’s start, illustrating the formula's practicality and accuracy.
Proof of Concept
Envision a circle with center O and radius OA.
Choosing three distinct points A, B, C on the circumference, we draw segments to construct triangle ABC.
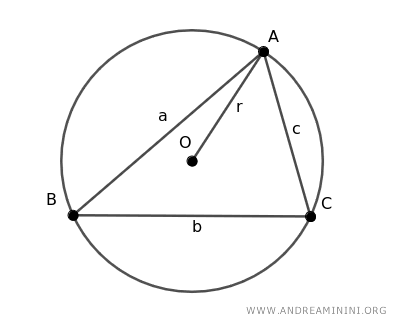
Next, the circle's diameter (d) and the triangle's height (h) are outlined.
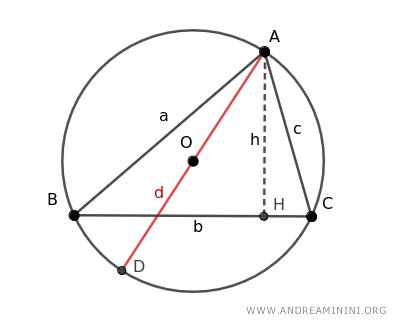
This configuration yields two right triangles, AHC and ABD.
- Triangle AHC forms a right angle because the height h is perpendicular to the base BC, serving as the triangle ABC's altitude.
- Triangle ABD is recognized as a right triangle since the segment AD is the circle's diameter, and it's a well-established fact that any triangle inscribed in a semicircle is a right angle triangle.
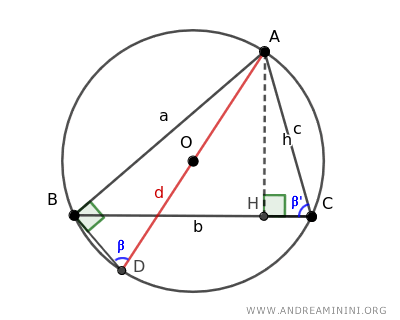
The congruence of certain angles in triangles AHC and ABD further underscores their similarity:
- The unmistakable right angle (90°).
- The matching acute angles β and β' are congruent because they are angles subtended by the same arc AB, thereby sharing the same measure.
As a result, according to the principles of triangle similarity, triangles AHC and ABD share proportional sides alongside their congruent angles, demonstrating that they are indeed similar.
$$ AHC \approx ABD $$
This similarity suggests that the ratios of corresponding sides are equal, hence the proportion:
$$ a : h = d : c $$
Given that the diameter d equals twice the radius (2r), we can express this relationship as:
$$ a : h = 2r : c $$
Converting this proportion into an equivalent fraction:
$$ \frac{a}{h} = \frac{2r}{c} $$
Allows us to isolate the radius:
$$ r = \frac{ac}{2h} $$
To further simplify, by multiplying and dividing the right-hand side by b, we arrive at:
$$ r = \frac{ac}{2h} \cdot \frac{b}{b} $$
$$ r = \frac{abc}{2hb} $$
Considering that the product hb equals twice the triangle's area (since A=hb/2), we find that hb=2A, leading to:
$$ r = \frac{abc}{2 \cdot (2A)} $$
$$ r = \frac{abc}{4A} $$
This logical progression culminates in demonstrating that the radius of the circumscribed circle around a triangle is precisely the product of the triangle's sides divided by four times its area.
The proof, thus, not only illustrates the formula’s validity but also enriches our understanding of the geometric relationship between a triangle and its circumscribed circle.
