Exterior Angle Theorem for Triangles

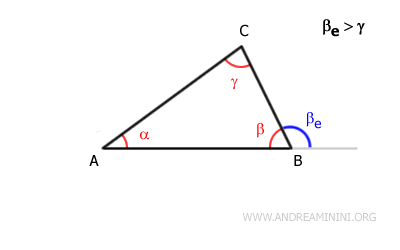
In any triangle, an exterior angle (β_e) is greater than either of the non-adjacent interior angles (α and γ)

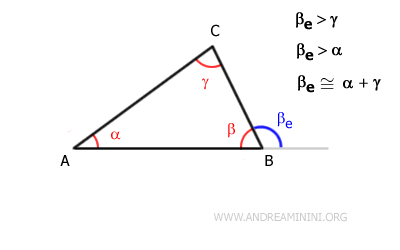
because every exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles $$ \beta_e \cong \alpha + \gamma $$

This is a universal theorem that applies to any triangle.

For example, in triangle ABC, the exterior angle at vertex B, β_e, is greater than both interior angles α and γ.

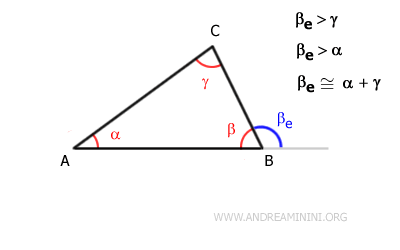
Therefore, in triangle ABC, the exterior angle β_e is larger than any interior angle other than β.

Proof

Consider a triangle ABC.

I extend segment AB beyond point B, creating an exterior angle $ \beta_e $ corresponding to the interior angle $ \beta $.

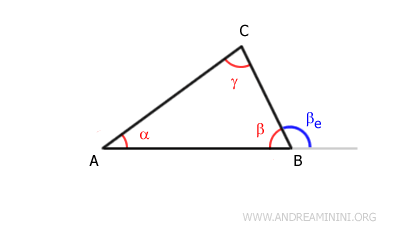
Next, I draw segment $ BE $, parallel to segment $ AC $, passing through vertex $ B $.

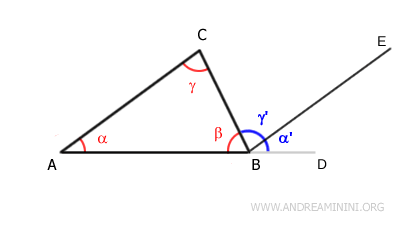
By construction, the exterior angle $ \beta_e $ is the sum of angles $ \alpha' $ and $ \gamma' $:

$$ \beta_e = \alpha' + \gamma' $$

According to the Parallel Lines Theorem, since the lines through $ BE $ and $ AC $ are parallel and intersected by transversal $ CB $, the alternate interior angles are congruent:

$$ \gamma = \gamma' $$

These same parallel lines $ BE $ and $ AC $ are also intersected by transversal $ AB $. Applying the Parallel Lines Theorem once again, the corresponding angles are congruent:

$$ \alpha = \alpha' $$

Note. The same theorem was applied to the parallel lines $ BE $ and $ AC $, but using two different transversals: first $ CB $, then $ AB $.

This demonstrates that the exterior angle $ \beta_e $ is equal to the sum of the two interior angles of the triangle that are not adjacent to $ \beta $:

$$ \beta_e = \alpha' + \gamma' = \alpha + \gamma $$

Since $ \beta_e = \alpha + \gamma $, it follows that the exterior angle $ \beta_e $ is necessarily greater than either $ \alpha $ or $ \gamma $ taken individually:

$$ \beta_e > \alpha $$

$$ \beta_e > \gamma $$

This proves that the exterior angle is greater than each of the non-adjacent interior angles and is exactly equal to their sum.

Alternative Proof

A] The Exterior Angle is Greater Than the Non-Adjacent Interior Angles

Consider a generic triangle ABC

Let's examine the exterior angle at vertex B, which we'll call β_e from now on.

We need to demonstrate that the exterior angle β_e is greater than the non-adjacent interior angles α and γ.

First Part

Identify the midpoint M of side BC adjacent to angle β and draw the median AM.

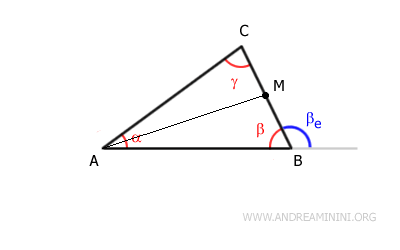
This gives us two congruent segments, BM and CM

$$ BM \cong CM $$

Extend segment AM by adding another segment ME such that AM = ME, effectively doubling its length.

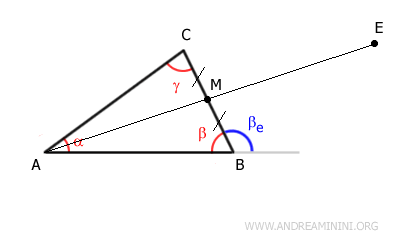
Recapping, the following sides are congruent:

$$ BM \cong CM $$

$$ AM \cong ME $$

Now, connect points B and E by adding segment BE to the construction.

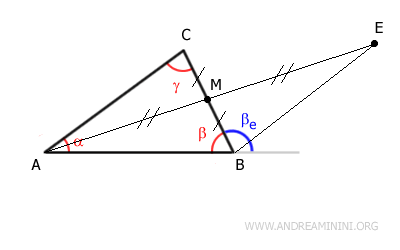
At point M, two segments intersect forming two congruent vertical angles θ₁ ≅ θ₂

$$ \theta_1 \cong \theta_2 $$

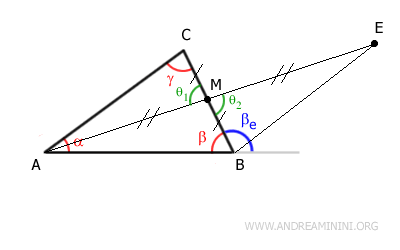
Therefore, according to the first congruence theorem, triangles AMC and BME are congruent because they have two congruent sides BM ≅ CM and AM ≅ ME, and the angle between them is congruent θ₁ ≅ θ₂.

$$ AMC \cong BME $$

Thus, triangles AMC and BME have congruent sides and angles in the same order.

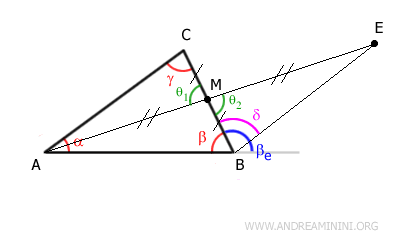
To conclude the proof, it's important to note that angles γ and δ are congruent:

$$ \gamma \cong \delta $$

Angle δ is smaller than the exterior angle β_e because segment BE divides angle β_e

$$ \delta < \beta_e $$

Knowing that angles γ and δ are congruent (γ ≅ δ), we can deduce that angle γ is also smaller than the exterior angle β_e

$$ \gamma < \beta_e $$

Therefore, the exterior angle β_e is greater than the interior angle γ

Second Part

Next, we need to perform a similar operation to show that the exterior angle β_e is also greater than the other non-adjacent interior angle, α.

Identify the midpoint M of segment AB adjacent to angle β and draw the median CM.

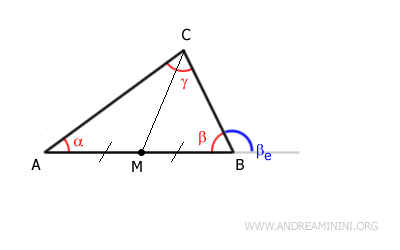
Consequently, the two segments AM and BM are congruent:

$$ \overline{AM} \cong \overline{BM} $$

Extend segment CM by adding another segment MF of equal length:

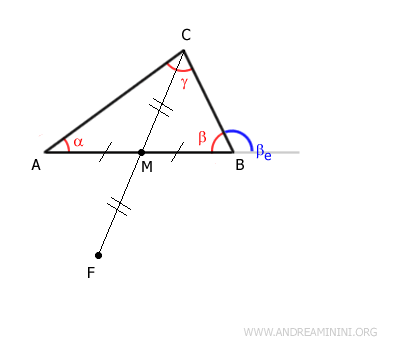
Therefore, segments CM and MF are congruent:

$$ \overline{CM} \cong \overline{MF} $$

Recapping, the following sides are congruent:

$$ \overline{AM} \cong \overline{BM} $$

$$ \overline{CM} \cong \overline{MF} $$

Connect points B and F by adding segment BF to the construction.

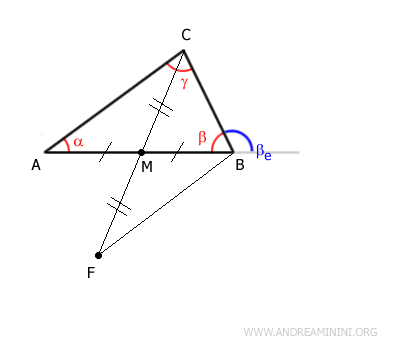
At point M, two segments AB and CF intersect forming two congruent vertical angles θ₁ ≅ θ₂

$$ \theta_1 \cong \theta_2 $$

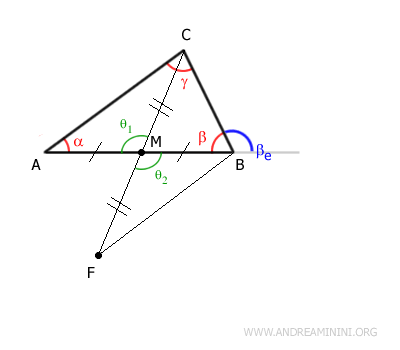
Thus, according to the first congruence theorem, triangles AMC and BMF are congruent because they have two congruent sides CM ≅ FM and AM ≅ BM, and the angle between them is congruent θ₁ ≅ θ₂.

$$ AMC \cong BMF $$

Thus, triangles AMC and BMF have congruent sides and angles in the same order.

Importantly , angle α is congruent to angle δ (purple):

$$ \alpha \cong \delta $$

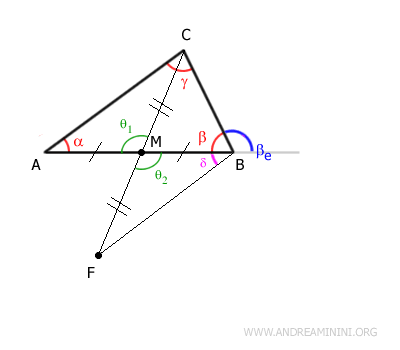
To compare angle β_e with angle δ, extend segment BC

Then, knowing that vertical angles are equal, project an angle congruent to β_e:

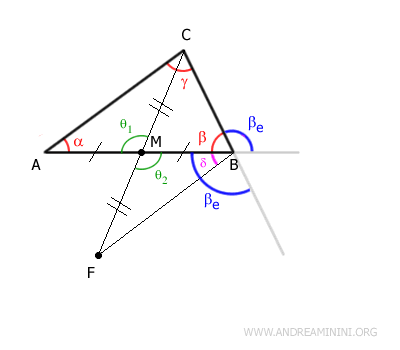
It becomes evident that the exterior angle β_e is greater than angle δ because segment BF divides angle β_e

$$ \delta < \beta_e $$

Knowing that angle δ is congruent to interior angle α (δ ≅ α), we deduce that the exterior angle β_e is greater than the interior angle α.

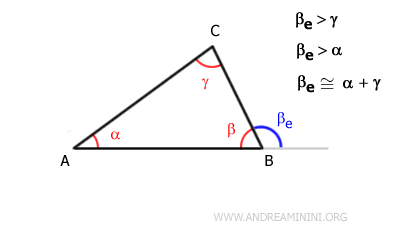
Conclusion

In a triangle, the exterior angle β_e is greater than the non-adjacent interior angles α and γ.

This proves the exterior angle theorem for a triangle.

B] The Exterior Angle is Equal to the Sum of the Non-Adjacent Interior Angles

Next, we need to show that the exterior angle is equal to the sum of the non-adjacent interior angles.

Consider triangle ABC and the exterior angle β_e

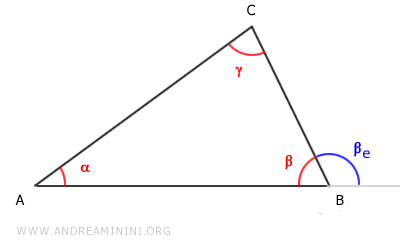
Draw lines passing through the segments of the triangle and name them a, b, c:

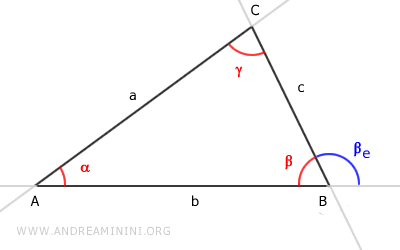
Draw line d parallel to segment AC passing through vertex B of the triangle.

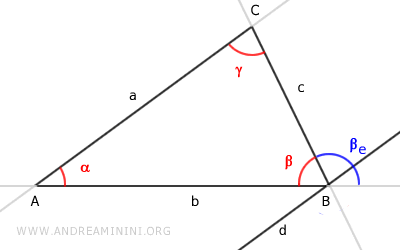
Now, we can consider the exterior angle as the sum of two angles β_e = β_e' + β_e''

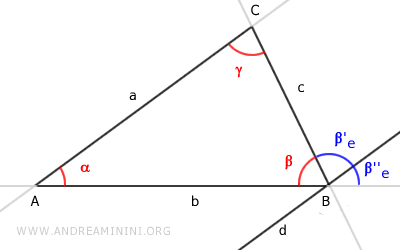
Angle β'_e is an alternate interior angle of the parallel lines a || d cut by line c.

By the parallel lines theorem, the alternate interior angles γ and β'_e are congruent, i.e., γ ≅ β'_e.

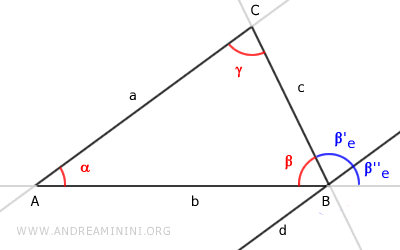
Angle β''_e is a corresponding angle of the parallel lines a || d cut by line b.

By the parallel lines theorem, the corresponding angles α and β''_e are congruent, i.e., α ≅ β''_e.

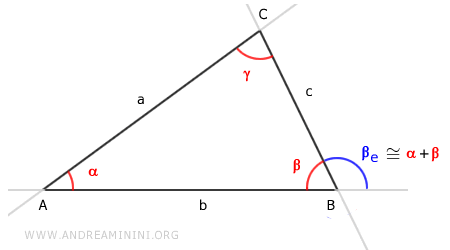
Knowing that the exterior angle is the sum β_e = β_e' + β_e'' and that angles γ ≅ β'_e and α ≅ β''_e are congruent:

$$ \begin{cases} \beta_e \cong \beta'_e + \beta''_e \\ \\ \gamma \cong \beta'_e \\ \\ \alpha \cong \beta''_e \end{cases} $$

We deduce that the exterior angle β_e is equal to the sum of the non-adjacent interior angles α + β of the triangle.

$$ \beta_e \cong \beta'_e + \beta''_e $$

$$ \beta_e \cong \beta + \alpha $$

Therefore, the exterior angle β_e = α + β is equal to the sum of the non-adjacent interior angles of the triangle.

Notes

Additional observations and corollaries related to the topic.

• The sum of a triangle’s interior angles is 180°
  The sum of the interior angles of any triangle is always 180°, which corresponds to a straight angle. In other words, this is a geometric invariant - a property that remains constant, no matter the type or shape of the triangle.
  
  

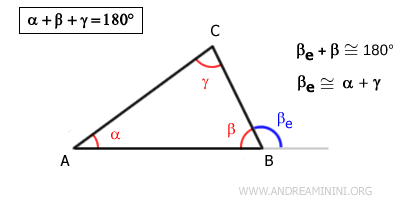
  Proof. This result can be derived by noting that each interior angle and its corresponding exterior angle together form a straight angle. For example: $$ \beta + \beta' = 180° $$ Moreover, the exterior angle is equal to the sum of the two non-adjacent interior angles: $ \beta' = \alpha + \gamma $. It follows that the sum of all three interior angles must always equal a straight angle: $$ \beta + (\alpha + \gamma) = 180° $$ $$ \alpha + \beta + \gamma = 180° $$

• The sum of two interior angles is always less than a straight angle
  This fundamental corollary follows from the fact that an exterior angle of a triangle is always greater than either of the two non-adjacent interior angles. In other words, $ \alpha + \gamma < 180° $.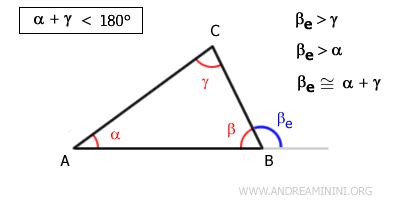

  

  Proof. By the exterior angle theorem, we know that the exterior angle \( \beta_e \) is greater than the non-adjacent interior angle \( \gamma \): $$ \gamma < \beta_e $$ Adding \( \beta \) to both sides of the inequality gives: $$ \gamma + \beta < \beta_e + \beta $$ Since \( \beta \) and \( \beta_e \) are supplementary, their sum forms a straight angle: $$ \beta + \beta_e = 180^\circ $$ Substituting this into the inequality, we get: $$ \gamma + \beta < 180^\circ $$ This confirms that the sum of any two interior angles in a triangle is always less than a straight angle. Using the same argument, we can also conclude that the other two pairs, $ \alpha + \gamma $ and $ \alpha + \beta $, are also less than $ 180^\circ $.

• A triangle can have at most one right or one obtuse angle
  This follows directly from the fundamental property that the sum of a triangle’s interior angles is always 180°.

  Note. If a triangle had two right angles (90° + 90° = 180°), there would be no room for a third angle, which is impossible. Likewise, if a triangle had two obtuse angles (each greater than 90°), their sum would exceed 180°, which contradicts the angle sum property. Therefore, a triangle can have at most one right angle or one obtuse angle. The remaining two angles must be acute (less than 90°) to ensure the total remains 180°.

• Further Corollaries
  The exterior angle theorem provides the foundation for several useful corollaries concerning triangles:
  • In a right triangle, the two acute angles are complementary
    Since the sum of the interior angles of any triangle is 180°, if one angle measures 90°, the sum of the remaining two angles must also be 90°.
  • In an equilateral triangle, each interior angle measures 60°
    An equilateral triangle has all sides and angles congruent. Given that the interior angles of a triangle always sum to 180°, dividing this total equally among the three angles results in each angle measuring 60°.
  • If two triangles have two congruent interior angles, their third angles must also be congruent
    Since the interior angles of a triangle always sum to 180°, if two triangles share two congruent angles, the third angle must necessarily be congruent as well.

And so on.