Incenter of a Triangle

The incenter of a triangle is the point where the angle bisectors of the triangle intersect, and it serves as the center of the triangle's inscribed circle (incircle).

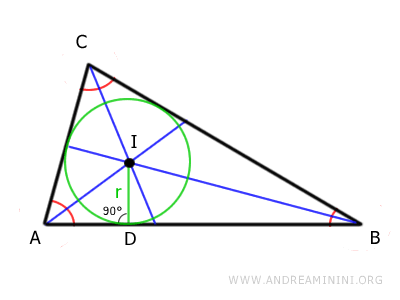
The primary feature of the incenter (I) is that it is equidistant from all three sides of the triangle.

This distance (ID) is the radius of the circle inscribed in the triangle, known as the incircle.

The inscribed circle is tangent to all three sides of the triangle, meaning it touches them without crossing.

The radius of the circle inscribed in the triangle is also called the inradius.

How to Find the Incenter

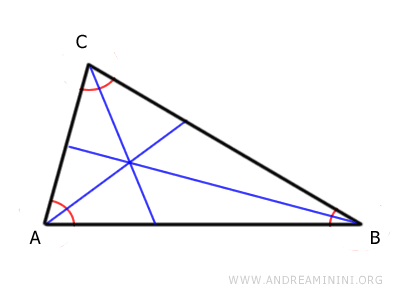
To find the incenter, draw the bisector of each interior angle of the triangle.

The angle bisector is the line that divides each angle into two equal parts.

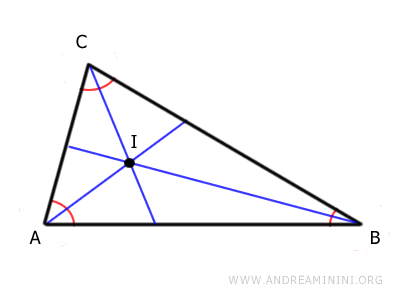
The point where the bisectors intersect (I) is called the incenter and lies inside the triangle.

Finally, draw a perpendicular segment (ID) from the incenter (I) to any side of the triangle. In this example, we choose side AB.

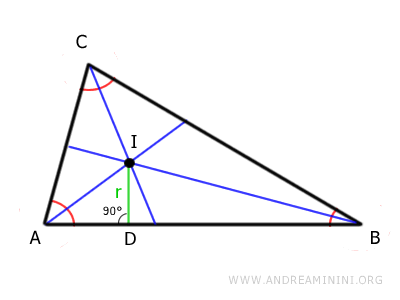
This segment is called the inradius and it is the radius of the circle inscribed in the triangle (the incircle).

The center of the inscribed circle is the incenter.

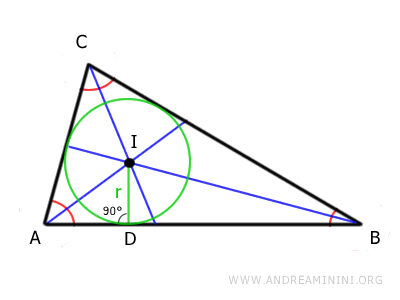
One key feature of the incircle is that it is tangent to all three sides of the triangle.

The Proof

Consider a triangle ABC.

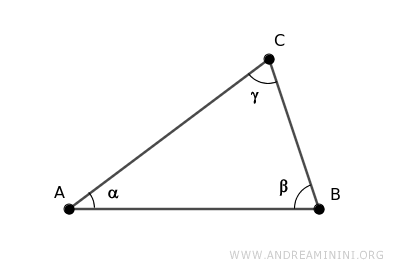
Draw the bisectors of angles α and β.

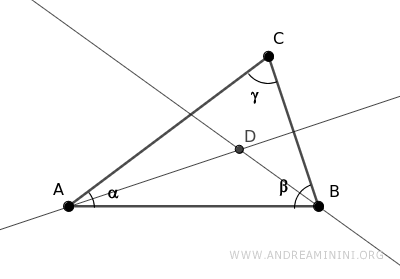
Knowing that the sum of the angles in a triangle is always 180° (a straight angle),

$$ \alpha + \beta + \gamma = 180° $$

we can deduce that the sum of angles α and β is less than 180°.

$$ \alpha + \beta < 180° $$

Therefore, the sum of half of angles α and β is also less than 180°, ensuring that the bisectors of angles α and β intersect at point D.

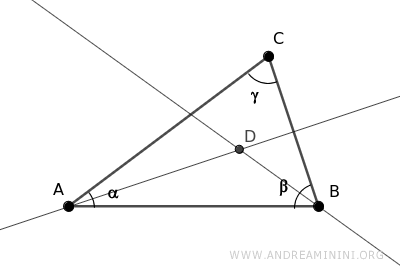
Draw perpendicular segments from point D to the sides of the triangle.

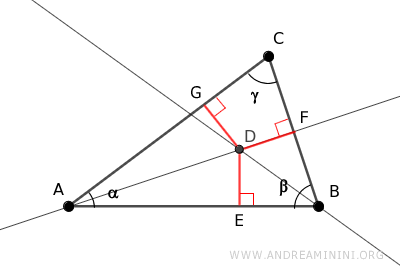
Segments DE≅DF are congruent because point D lies on the bisector of angle β, making it equidistant from the sides of angle β.

$$ \overline{DE} \cong \overline{DF} $$

Similarly, segments DE≅DG are congruent because point D lies on the bisector of angle α, making it equidistant from the sides of angle α.

$$ \overline{DE} \cong \overline{DG} $$

By the transitive property, if DE≅DF and DE≅DG, then segments DF≅DG are also congruent.

$$ \overline{DF} \cong \overline{DG} $$

This means the point of intersection D is equidistant from the sides of angle γ, so it lies on the bisector of angle γ.

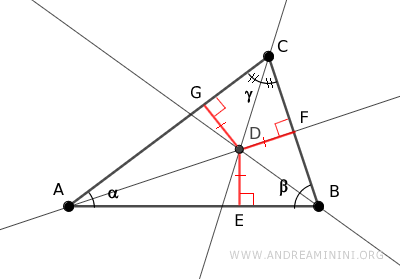
This proves that point D lies on all the bisectors of the triangle's angles.

Observations

Here are some observations and properties of the incenter:

• Every triangle can be circumscribed by a circle with the incenter as its center.
• The incenter is equidistant from all three sides of the triangle. This distance is the radius of the inscribed circle.
• The position of the incenter varies depending on the shape of the triangle. For instance, in an equilateral triangle, the incenter coincides with the centroid, circumcenter, and orthocenter.
• The incenter divides each angle bisector into two segments that are proportional to the sides of the triangle adjacent to the vertex.
• The inscribed circle (incircle) with the incenter as its center is tangent to the sides of the triangle.

And so on.