Longest Side and Largest Angle in Triangles

In any non-equilateral triangle, the longest side is opposite the largest angle, and vice versa.

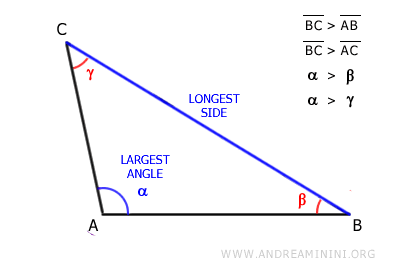
This theorem holds true for all triangles except equilateral ones.

It doesn't apply to the equilateral triangle because an equilateral triangle has three equal sides and three equal angles, so there is no longest side or largest angle.

A Practical Example

Let's take a scalene and obtuse triangle as an example.

The largest angle is angle alpha at vertex A.

$$ \alpha > \beta $$

$$ \alpha > \gamma $$

The side opposite the largest angle alpha is side AB, which is also the longest side of the triangle.

$$ \overline{BC} > \overline{AB} $$

$$ \overline{BC} > \overline{AC} $$

And the reverse is also true.

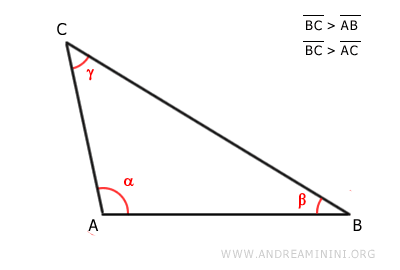
The Proof

Starting with the assumption that side BC is the longest side of triangle ABC.

$$ \overline{BC} > \overline{AC} $$

$$ \overline{BC} > \overline{AB} $$

We need to prove that the angle opposite the longest side BC, which is angle α, is larger than the other two angles.

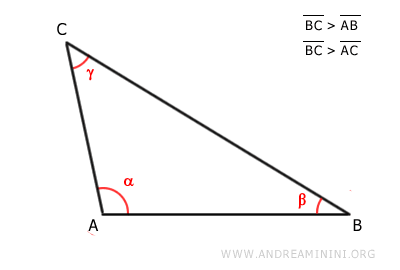
Using a compass centered at vertex C and a radius of CA, draw an arc that intersects side CB.

Let’s call this point D.

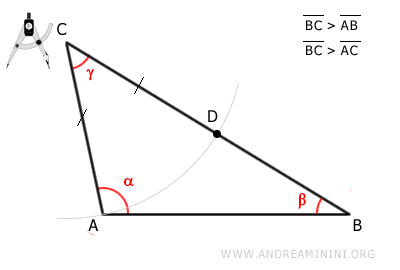
Therefore, segment CD is congruent to segment AC.

$$ \overline{CD} \cong \overline{AC} $$

Draw a segment AD.

Points ACD form an isosceles triangle since sides AC and CD are congruent.

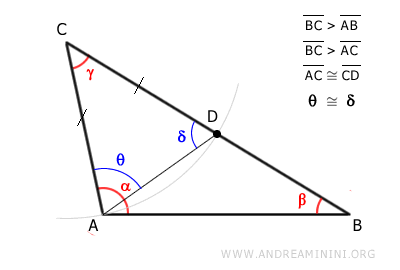
As an isosceles triangle, triangle ACD has two congruent angles, δ and θ, adjacent to base AD.

$$ δ \cong θ $$

Angle δ is an external angle of triangle ABD.

According to the exterior angle theorem, the external angle δ is larger than the other two non-adjacent interior angles, β and α-θ, of triangle ABD.

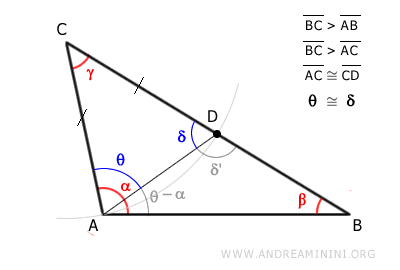
In particular, it’s useful to note that angle δ is greater than β.

$$ \delta > \beta $$

Since angles δ and θ are congruent (δ ≅ θ), angle θ is also greater than β. 

$$ θ > \beta $$

Angle θ is smaller than angle α (i.e., θ < α) because it shares one side, and the other side is within angle α.

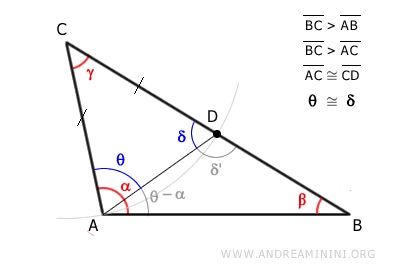
Therefore, angle α is greater than angle β

$$ \alpha > \beta $$

Now we need to prove that angle α is also greater than angle γ.

Returning to the initial triangle ABC, use a compass centered at point B to draw an arc with a radius of AB, intersecting side AC.

This identifies point E.

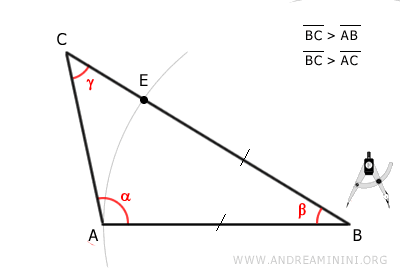
Consequently, segment EB is congruent to segment AB.

$$ \overline{EB} \cong \overline{AB} $$

Draw a segment AE.

Points ABE form an isosceles triangle since sides AB and EB are congruent.

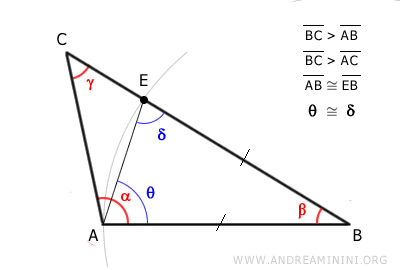
As an isosceles triangle, triangle ABE also has two congruent angles, δ and θ, adjacent to base AE.

$$ δ \cong θ $$

Angle δ is an external angle of triangle ACE.

According to the exterior angle theorem, the external angle δ is larger than the other two non-adjacent interior angles, γ and α-θ, of triangle ACE.

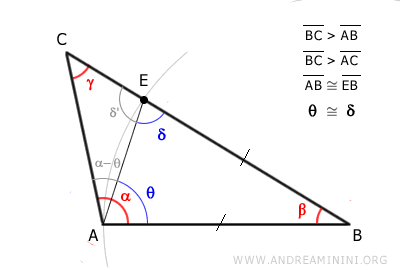
It's particularly useful to note that angle δ is greater than γ.

$$ \delta > \gamma $$

Since angles δ and θ are congruent (δ ≅ θ), angle θ is also greater than γ.

$$ θ > \gamma $$

Angle θ is smaller than angle α (i.e., θ < α).

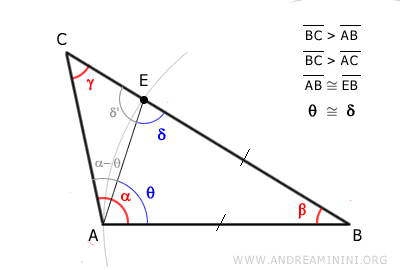
Therefore, angle α is greater than angle γ

$$ \alpha > \gamma $$

In conclusion, angle α opposite the longest side BC is larger than both angle β and angle γ.

Thus, angle α is the largest angle in triangle ABC.

Notes

Here are some notes and corollaries of the theorem:

• In a right triangle, the hypotenuse is always the longest side compared to each leg.
• In an obtuse triangle, the side opposite the obtuse angle is always the longest side compared to the other two sides.
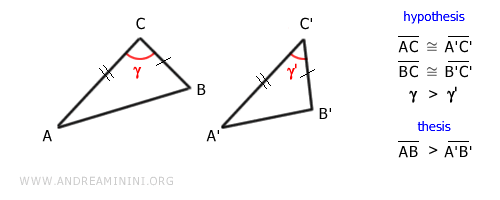
• Corollary
  If two triangles have two congruent sides in the same order (e.g., AC ≅ A'C' and BC ≅ B'C') but different included angles, the one with the larger angle (e.g., γ > γ') also has the longer third side (e.g., AB > A'B').
  

And so on.