Criteria for Triangle Congruence
The three criteria for triangle congruence help determine if two triangles are congruent using only a few specific details.
In general, according to the definition of congruence, two geometric figures are congruent if they can be exactly overlapped through a rigid motion.
This straightforward rule applies to triangles but is quite demanding because it requires complete information about them.
However, there are three criteria for triangle congruence that can verify if two triangles are congruent using only three specific pieces of information.
Why use congruence criteria? Triangle congruence criteria compare pairs of sides and angles, avoiding the need to compare all pairs of points. This makes the process faster and relies only on some available information.
First Criterion for Triangle Congruence
Two triangles are congruent if they have two sides and the included angle between them congruent in the same order.
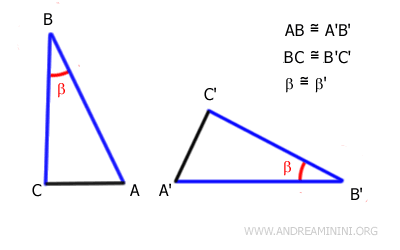
In practice, triangles are congruent if they have two sides of the same length and the angle between them is of the same measure.
This is also known as the SAS (Side-Angle-Side) criterion.
However, the term SAS should not be taken literally; the angle must be included between the sides.
If the congruent angle is not the one included between the two sides, the triangles may not be congruent.
For example, consider triangle ABC. Draw a circle with radius AC and center A. The arc intersects the extension of segment AC at point D, forming another triangle ACD.
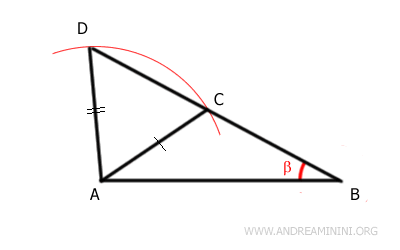
The two triangles ABC and ABD are not congruent. Although they have two congruent sides AB ≅ AB and AC ≅ AD, and the angle β is congruent, this angle is not included between the two sides. Therefore, having two congruent sides and an angle not included between them is not enough to declare the triangles congruent.
The first congruence criterion is considered a postulate.
Second Criterion for Triangle Congruence
Two triangles are congruent if they have two angles and the adjacent side between them congruent in the same order.
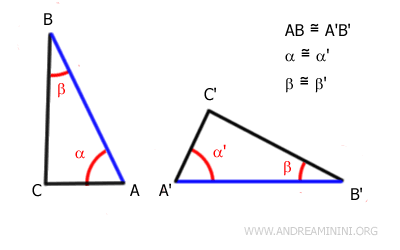
In other words, triangles are congruent when they have two angles of the same measure and the adjacent side between these angles of the same length.
This is also known as the ASA (Angle-Side-Angle) criterion.
This criterion is a theorem because it can be proven.
According to Euclid's fifth postulate, the sum of the interior angles of a triangle is always equal to a straight angle (180°). Therefore, if two angles are known, the measure of the third angle is also known by subtraction.
The second congruence criterion also has a generalized form called the "generalized second criterion" or "fourth criterion for triangle congruence".
Two triangles are congruent if they have two angles and one congruent side in the same sequence, with the side not necessarily included between the two angles.
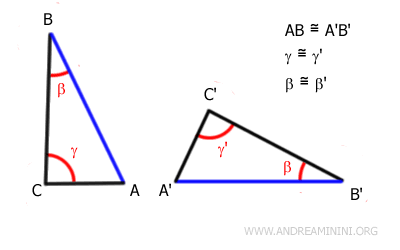
In this case, the congruent side can be any side; it does not have to be the side included between the angles.
Third Criterion for Triangle Congruence
Two triangles are congruent if they have all three sides congruent.
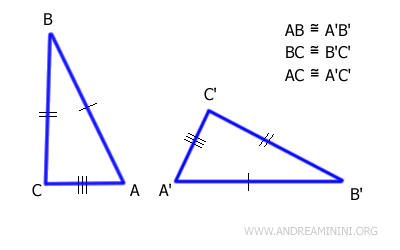
In practice, triangles are congruent if they have sides of the same length.
This is also known as the SSS (Side-Side-Side) criterion.
This criterion is also a theorem because it can be proven.
Note. The congruence of all angles (AAA) is a necessary but not sufficient condition for triangle congruence. Two triangles could have congruent angles but sides of different lengths. In this case, the two triangles are not congruent because they cannot be overlapped. The two triangles have the same shape but one is larger than the other. Conversely, two triangles with congruent sides (SSS) always have congruent angles. Therefore, the AAA criterion is not a criterion for triangle congruence.
And so on.
