Midpoint Theorem of a Triangle
In a triangle, the segment joining the midpoints of two sides is parallel to the third side and is half as long.
In other words, if you draw a line connecting the midpoints of two sides of a triangle, this line will be parallel to the third side and half its length.
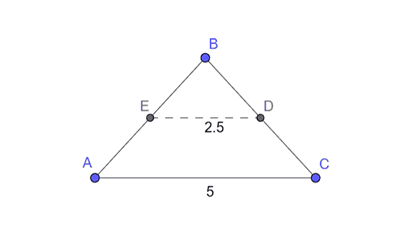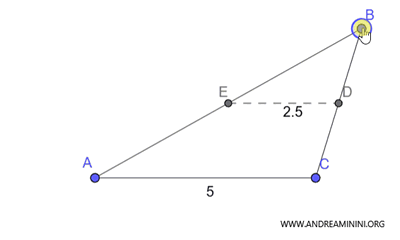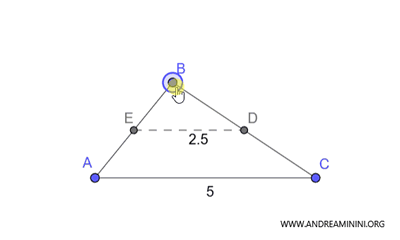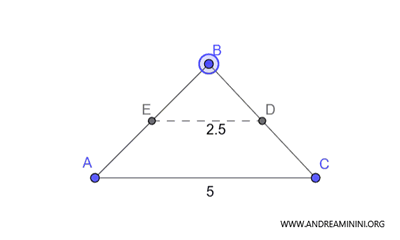
This property holds true for all types of triangles.
An Example
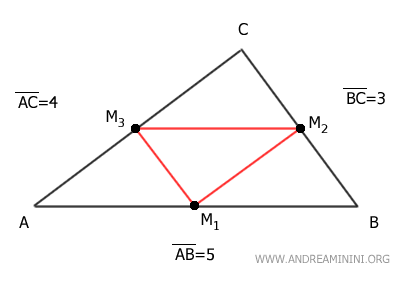
Consider the triangle ABC with the following side lengths: AB=5, BC=3, and AC=4.
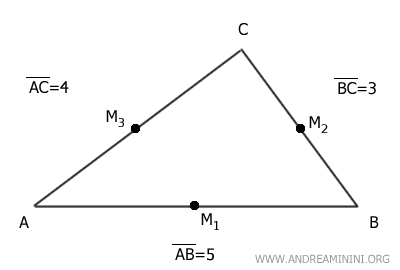
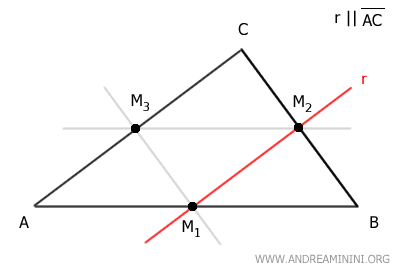
Each side has its midpoint, dividing it into two equal parts: M1 on side AB, M2 on side BC, and M3 on side AC.
Now, draw the segment between midpoint M2 of side BC and midpoint M3 of side AC.
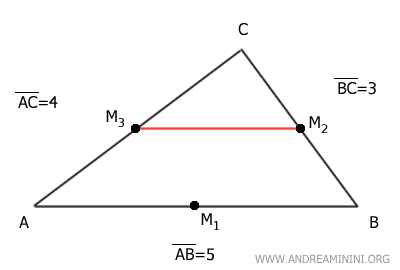
This segment M2M3 is parallel to the remaining side AB of the triangle.
Moreover, the length of segment M2M3 is half that of side AB, which is 2.5.
$$ \overline{M_2M_3} = \frac{\overline{AB}}{2} = \frac{5}{2} = 2.5 $$
Similarly, the segment between midpoints M1 and M3 is parallel to side BC and half its length, which is 1.5.
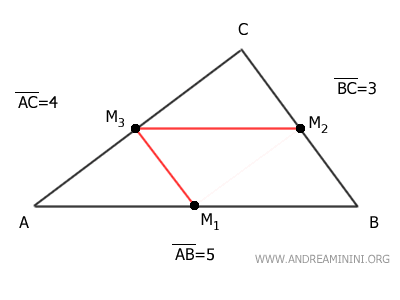
Finally, the segment between midpoints M1 of side AB and M2 of side BC is parallel to side AC and half its length, which is 2.
Corollary
A line passing through the midpoint M of one side of a triangle and parallel to another side will also pass through the midpoint of the remaining side.
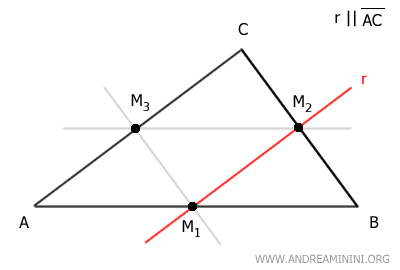
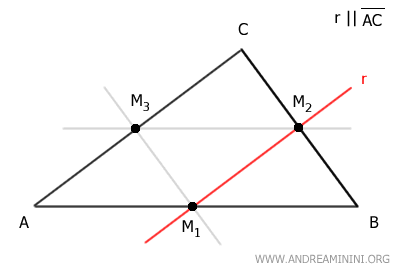
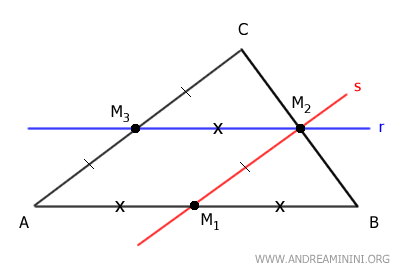
For example, draw the line r parallel to side AB that passes through the midpoint M2 of side BC.
This line also passes through the midpoint M3 of side AC.
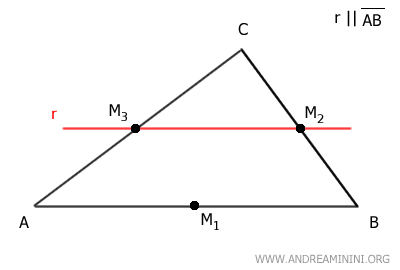
This relationship is reciprocal. If I draw a line r parallel to AB passing through midpoint M3, it will also pass through midpoint M2 of side BC.
Similarly, if I draw a line parallel to side BC passing through midpoint M3 of side AC, it will also pass through midpoint M1 of side AB, and vice versa.
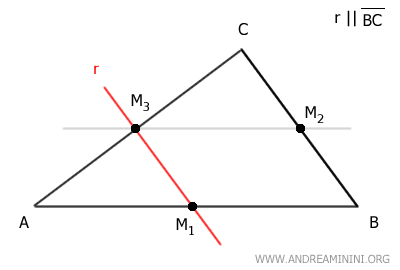
Finally, if I draw a line parallel to side AC passing through midpoint M1 of side AB, it will also pass through midpoint M2 of side BC, and vice versa.
Proof
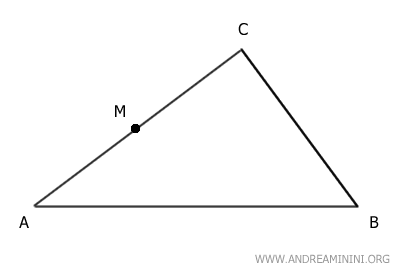
Consider a triangle ABC and point M on side AC.
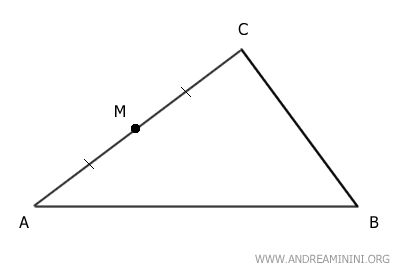
Point M is the midpoint of side AC, thus dividing AC into two congruent segments AM ≅ CM.
The proof is divided into three parts:
A] If a line is parallel to one side and passes through the midpoint of another side of a triangle, it also passes through the midpoint of the remaining side.
Draw two lines r and s parallel to side AB, passing through points M and C, respectively.
Line r intersects side BC at point D.
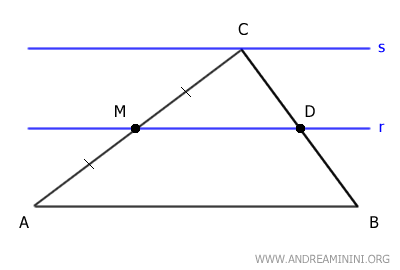
Now, consider side AC and lines r and s as a set of parallel lines, and sides AC and BC as two transversals.
According to the theorem of parallel lines, the corresponding segments of the transversals are directly proportional.
Therefore, if AM ≅ CM, then BD ≅ CD.
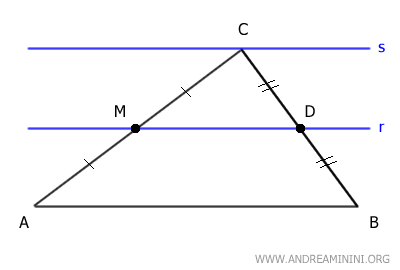
The segments BD and CD are congruent, so point D is the midpoint of side BC.
This demonstrates that a line parallel to one side of a triangle passing through the midpoint of another side also passes through the midpoint of the remaining side.
In conclusion, if a segment is parallel to one side of a triangle and starts from the midpoint of another side, it ends at the midpoint of the third side.
B] If a line passes through the midpoints of two sides, it is parallel to the third side of the triangle.
Now, let's prove the converse: if a line passes through the midpoints of two sides, it is parallel to the third side of the triangle.
Consider triangle ABC and a line r passing through midpoints M2 of side BC and M3 of side AC.
We need to prove that line r is also parallel to the remaining side AB.
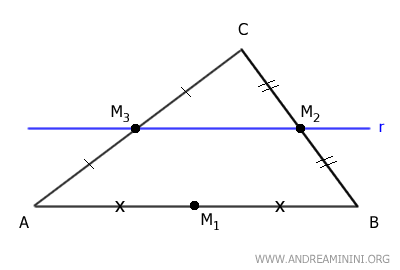
To prove this, we use a proof by contradiction.
Assume that line r passes through the midpoints of sides BC and AC but is not parallel to side AB.
If this were true, then according to the theorem of parallel lines, there must be another line s parallel to AB such that
$$ \overline{AM_2} : \overline{CM_2} = \overline{BM_2} : \overline{CM_2} $$
Since AM2 ≡ CM2, this would mean that line s intersects side BC at another midpoint M'2 different from M2.
Therefore, side BC would have two midpoints, one from the initial hypothesis M2 and another by construction M'2.
Since this is not possible, we conclude that the hypothesis is false.
Hence, the converse is true, which means if a line passes through the midpoints of two sides of a triangle, it is parallel to the third side.
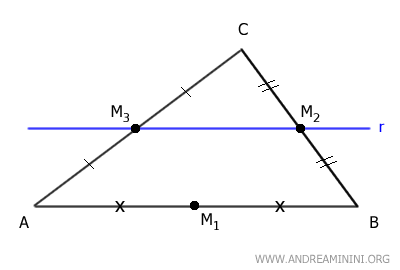
C] The segment between two midpoints has a length equal to half the length of the parallel side of the triangle.
In this final part of the proof, we need to show that the segment between two midpoints is half the length of the remaining side.
For example, we have already shown that the segment between midpoints M2 and M3 is parallel to the remaining side AB of the triangle and vice versa.
Draw a line s parallel to side AC passing through midpoint M2.
Since this line passes through M2 and is parallel to side AC, then by the previously proven theorem, this line must also pass through the midpoint of the remaining side, which is the midpoint M1 of side AB.
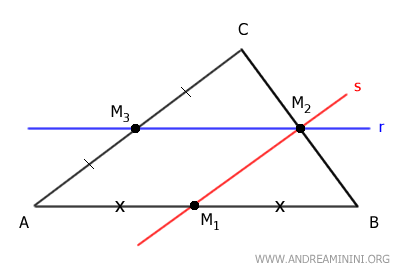
Now, the figure AM1M2M3 is a parallelogram, so it has congruent and parallel opposite sides.
$$ AM_1 \cong M_2 M_3 $$
$$ AM_3 \cong M_1 M_2 $$
From this, we deduce that segment M2M3 is congruent to segment AM1, which is half the length of side AB.
$$ AM_3 \cong \frac{\overline{AB}}{2} $$
This proves that the distance between the midpoints of two sides of a triangle is equal to half the length of the remaining side.
And so on.
