Sum of the Angles in a Triangle

The sum of the angles in a triangle is equal to a straight angle (180°).

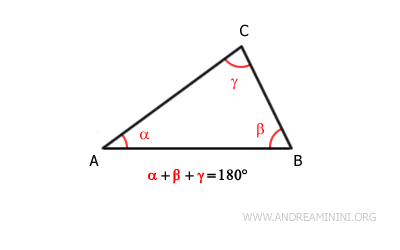
Therefore, the sum of the angles in any triangle is always 180°.

$$ \alpha + \beta + \gamma = 180° $$

Proof

Let's consider a generic triangle ABC.

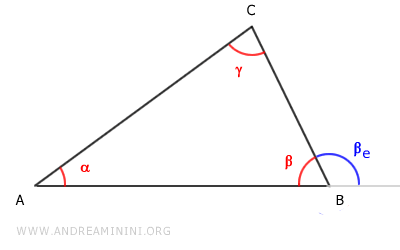
The exterior angle β_e is a supplementary angle to angle β because their sum is a straight angle (180°).

$$ \beta + \beta_e = 180° $$

According to the exterior angle theorem, an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles.

$$ \beta_e \cong \alpha + \gamma $$

Thus, combining the two pieces of information β_e + β = 180° and β_e ≅ α + γ

$$ \beta + \beta_e = 180° $$

$$ \beta + ( \alpha + \gamma ) = 180° $$

We conclude that the sum of the interior angles of a triangle is equal to a straight angle (180°).

$$ \alpha + \beta + \gamma = 180° $$

This proves the theorem that the sum of the angles in a triangle is 180°.

Alternative Proof

Consider a triangle ABC.

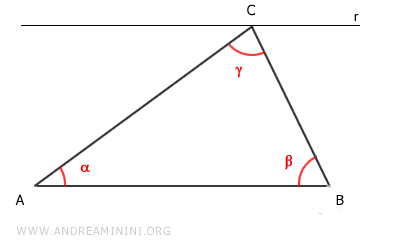
Draw a line parallel to side AB passing through vertex C of the triangle.

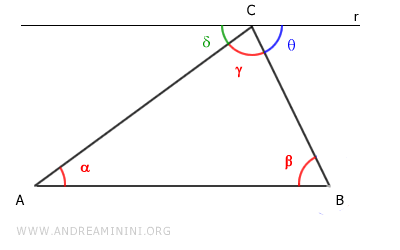
The angles δ + γ + θ = 180° add up to a straight angle (180°).

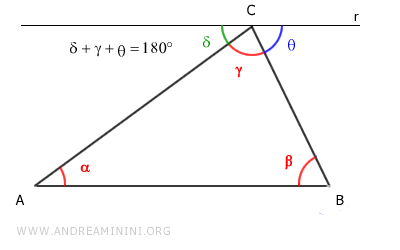
According to the parallel lines theorem, alternate interior angles are congruent.

• Alternate interior angles α ≅ δ are congruent with respect to the transversal AC.
• Alternate interior angles β ≅ θ are congruent with respect to the transversal BC.

Therefore, if δ + γ + θ = 180° and α ≅ δ, β ≅ θ, it follows that the sum α + β + γ = 180° is a straight angle.

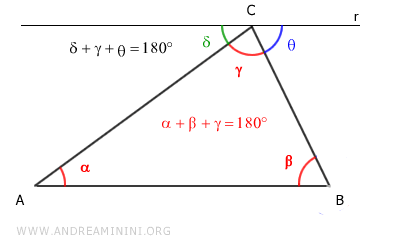
In conclusion, the sum of the interior angles of a triangle is 180°.

And so forth.