The Triangle Inequality Theorem

In any triangle, each side is shorter than the sum of the other two sides.

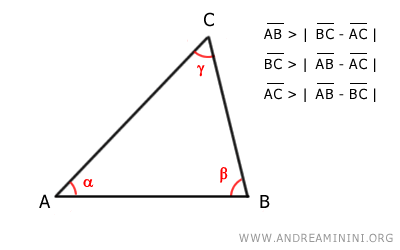
Moreover, each side is longer than the difference between the other two sides.

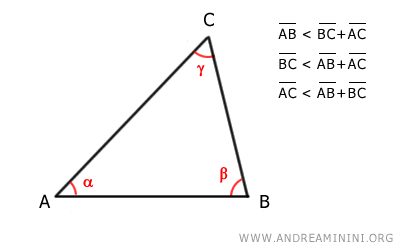
For instance, consider triangle ABC.

Side AB is shorter than the sum of sides BC and AC.

$$ \overline{AB} < \overline{BC}+\overline{AC} $$

The same rule applies to the other two sides:

$$ \overline{BC} < \overline{AB}+\overline{AC} $$

$$ \overline{AC} < \overline{AB}+\overline{BC} $$

A Practical Example

Consider a triangle ABC:

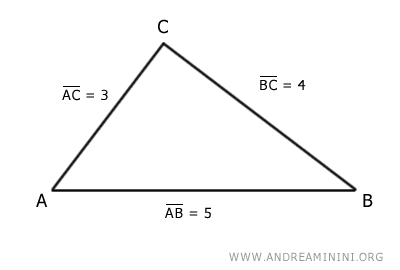
The sides of the triangle have the following lengths:

$$ \overline{AB} = 5 $$

$$ \overline{BC} = 4 $$

$$ \overline{AC} = 3 $$

Side AB, which is 5 units long, is shorter than the sum of the other two sides, AC and BC:

$$ 5 < 4 + 3 = 7 $$

Side AB is also longer than the difference between the other two sides, AC and BC:

$$ 5 > 4 - 3 = 1 $$

Side BC, which is 4 units long, is shorter than the sum of the other two sides, AB and AC:

$$ 4 < 5 + 3 = 8 $$

Side BC is also longer than the difference between the other two sides, AB and AC:

$$ 4 > 5 - 3 = 2 $$

Side AC, which is 3 units long, is shorter than the sum of the other two sides, AB and BC:

$$ 3 < 5 + 4 = 9 $$

Side AC is also longer than the difference between the other two sides, AB and BC:

$$ 3 > 5 - 4 = 1 $$

All the conditions of the triangle inequality are satisfied.

The Proof

Consider a triangle ABC where the longest side is AC.

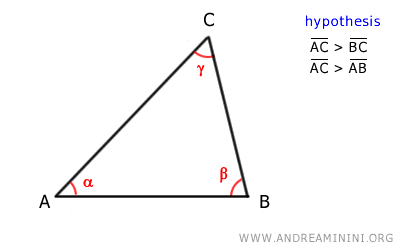
The initial assumptions are:

$$ \overline{AC} > \overline{BC} $$

$$ \overline{AC} > \overline{AB} $$

We need to show that side AC is shorter than the sum of the other two sides:

$$ \overline{AC} < \overline{BC} + \overline{AB} $$

Additionally, we need to show that side BC is longer than the difference between the other two sides:

$$ \overline{AC} - \overline{AB} < \overline{BC} $$

Extend side AB with a segment BD that is congruent to BC:

 

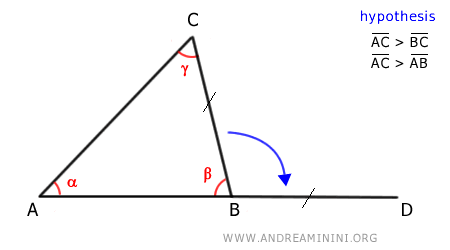
Then draw a segment CD connecting points C and D:

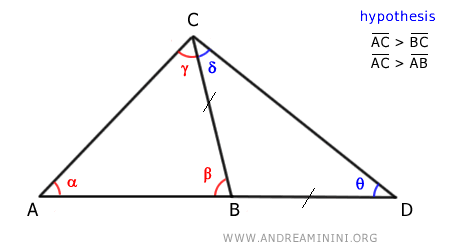
Triangle BDC is an isosceles triangle because it has two congruent sides .

Therefore, in an isosceles triangle, the base angles are congruent (δ≅θ):

$$ \delta \cong θ $$

It is immediately evident that the angle γ + δ is greater than δ:

$$ \gamma + \delta > \delta $$

Since the angles δ and θ are congruent, we deduce that the angle γ + δ is also greater than θ:

$$ \gamma + \delta > θ $$

Now, consider triangle ADC:

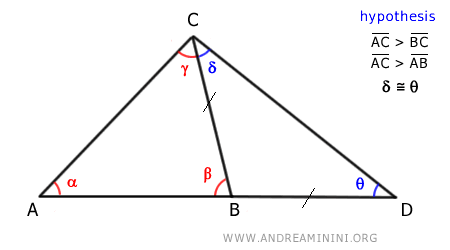
According to the theorem of the greater angle, in triangle ADC, side AC opposite angle θ is shorter than side AD opposite angle γ + δ:

$$ \overline{AC} < \overline{AD} $$

Knowing that side AD is the sum of segments AB and BD:

$$ \overline{AC} < \overline{AB} + \overline{BD} $$

Furthermore, knowing that sides BC and BD are congruent (BC ≅ BD):

$$ \overline{AC} < \overline{AB} + \overline{BC} $$

We have thus demonstrated that side AC is shorter than the sum of sides AB and BC in triangle ABC.

Now, apply the invariant property and subtract side AB from both sides of the inequality:

$$ \overline{AC} - \overline{AB} < \overline{AB} + \overline{BC} - \overline{AB} $$

$$ \overline{AC} - \overline{AB} < \overline{BC} $$

In this way, we have also demonstrated that side BC is longer than the difference between the other two sides of triangle ABC.

The Distance Between Three Points in Space

Generally, the triangle inequality theorem underlies another important distance theorem.

In a metric space, given any three points A, B, and C, the distance between any two points d(A,B) is less than or equal to the sum of the distances between the other two points d(B,C) + d(A,C). $$ d(A,B) \le d(B,C) + d(A,C) $$

In this case, we must also consider the equality scenario, which occurs when points A, B, and C are collinear.

Remarks

Some remarks on the triangle inequality theorem:

• Given three segments a, b, and c, constructing a triangle with these segments is possible only if each segment is shorter than the sum of the other two segments: $$ a < b+c $$ $$ b < a+c $$ $$ c < a+b $$

And so on.