Isosceles Triangle

An isosceles triangle is a type of triangle that has two sides of equal length, known as the legs or isosceles sides.

The third side of the isosceles triangle is called the base.

The two equal sides form two base angles that are also equal.

The angle opposite the base is known as the vertex angle.

Why is it called isosceles? The term "isosceles" comes from ancient Greek. It combines "isos," meaning "equal," and "skelos," meaning "leg." So, "isosceles" literally translates to "equal legs," accurately describing a triangle with two sides of equal length.

A Practical Example

Consider this triangle ABC.

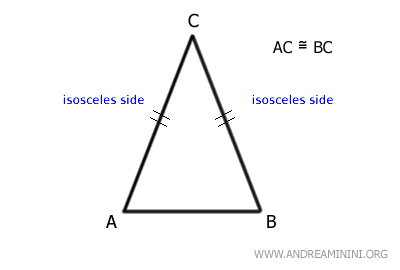
Sides AC and BC are congruent because they are the same length.

These are the "legs" or "isosceles sides" of the triangle.

Therefore, the non-congruent side AB is the base of the triangle.

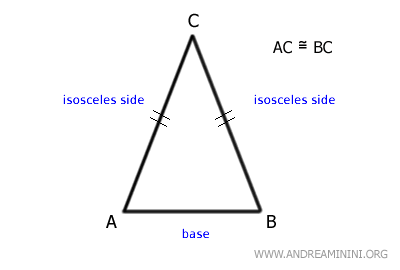
The two isosceles sides form two equal angles adjacent to the base.

These angles are also known as the "base angles".

The isosceles triangle ABC can also be referred to as "isosceles triangle with vertex C."

Observations

Here are some observations and properties of isosceles triangles:

• An isosceles triangle has two congruent sides (AC≅BC)
  

  

• The Isosceles Triangle Theorem

  An isosceles triangle has two equal base angles (α≅β). And vice versa.

  This is because, in a triangle, sides opposite equal angles are also equal.
  

  Note. The converse is also true. If a triangle has two equal angles, then it is an isosceles triangle.

• The base angles of an isosceles triangle are always acute
  
  The base angles of an isosceles triangle must be two acute angles because, being congruent, they cannot both be right or obtuse. A triangle cannot have more than one right or obtuse angle.
  

  Explanation. If the base angles were both right or obtuse, it would violate the theorem on the sum of two interior angles of a triangle, which states that a triangle always has at least two acute internal angles. Therefore, if two internal angles of a triangle are always acute, any triangle cannot have more than one right or obtuse angle.

• The Bisector in an Isosceles Triangle

  In an isosceles triangle, the bisector of the angle opposite the base coincides with the median, the height, and the perpendicular bisector of the base.

  
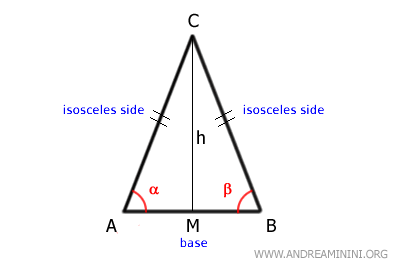
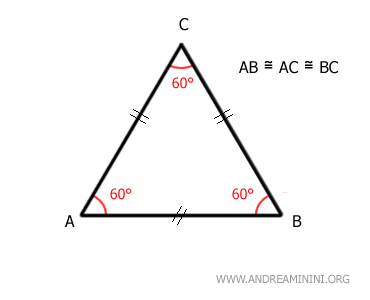
  The height (h) of the isosceles triangle from the vertex to the base creates two congruent right triangles (AMC≅BCM) and divides the base into two equal segments (AM≅BM).
• An equilateral triangle is a specific type of isosceles triangle where all three sides are equal in length. Therefore, an equilateral triangle is also isosceles, but the reverse is not necessarily true. In an equilateral triangle, any side can be considered the base. Additionally, it has three equal angles of 60°.
  
• The sum of the interior angles of any triangle, including the isosceles, is always 180 degrees.
• An isosceles triangle can be acute-angled, right-angled, or obtuse-angled.
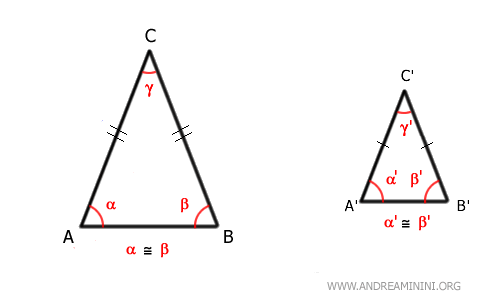
• Two isosceles triangles are similar if they have the same vertex angle
  Two isosceles triangles are considered similar if they have the same vertex angle, which is the angle between the equal sides. This is because in any triangle, the sum of the interior angles is always 180 degrees. If the vertex angles γ≅γ' are congruent, the base angles of both triangles are each equal to (180° - γ)/2. Consequently, the two triangles have all congruent angles and, according to the first similarity criterion for triangles, are similar, meaning they have the same shape but can have different sizes.
  

And so on.