Isosceles Triangle Theorem

A triangle is isosceles if and only if it has two congruent base angles.

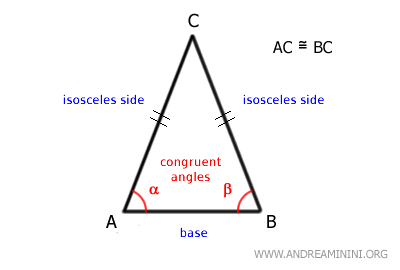
This follows from the fact that, in any triangle, sides opposite equal angles must also be equal.

Therefore, if a triangle is isosceles, then it has two congruent angles.

The converse is also true: if a triangle has two congruent angles, then it is an isosceles triangle.

In other words, having two congruent base angles is a necessary and sufficient condition for a triangle to be isosceles.

Proof

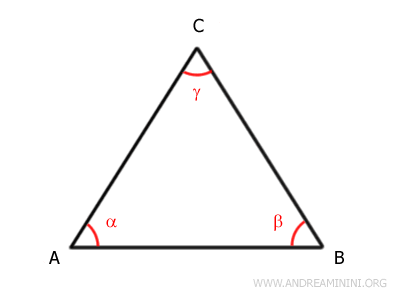
Let’s start by considering an isosceles triangle.

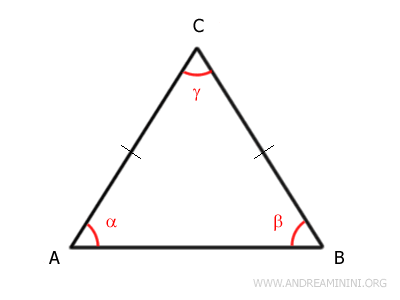
By definition, an isosceles triangle has two equal sides:

$$ \overline{AC} \cong \overline{BC} $$

Here, AC and BC are the congruent sides, while AB serves as the base.

Our goal is to prove that the base angles are also congruent.

To do this, we draw the angle bisector CD of γ, splitting it into two equal parts: γ₁ and γ₂.

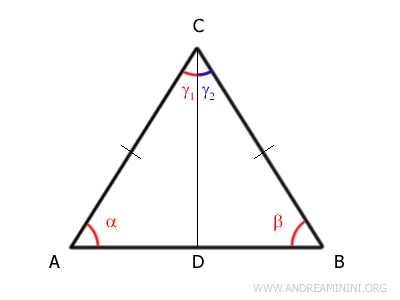
This creates two right triangles, ACD and BCD.

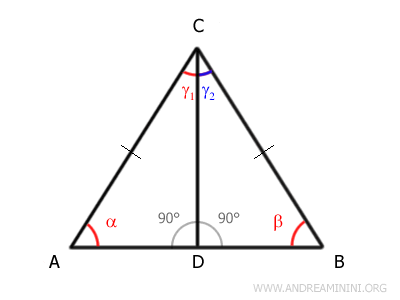
By the first congruence theorem, triangles ACD and BCD are congruent because they share two congruent sides (CD = CD, AC ≅ BC) and a congruent included angle (γ₁ ≅ γ₂).

• The two triangles share the side CD: $$ \overline{CD} \cong \overline{CD} $$
• Since ABC is an isosceles triangle, AC and BC are congruent: $$ \overline{AC} \cong \overline{BC} $$
• By construction, γ₁ and γ₂ are equal: $$ \gamma_1 \cong \gamma_2 $$

Since ACD and BCD are congruent, all corresponding sides and angles are also congruent.

In particular, this means that angles α and β are equal:

$$ \alpha \cong \beta $$

Thus, we have proven that an isosceles triangle always has congruent base angles.

Converse Proof

Now, let’s prove the converse: if a triangle has two congruent base angles, then it must be isosceles.

We begin with a triangle where two angles are equal (α ≅ β).

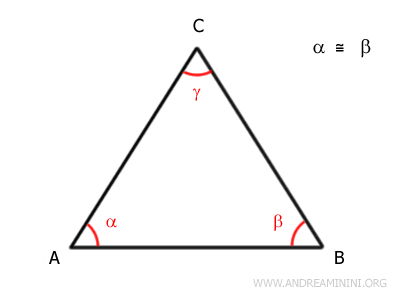
By assumption, α and β are congruent:

$$ \alpha \cong \beta $$

We need to show that this implies the triangle has two equal sides.

To do this, we extend sides AC and BC by adding congruent segments AD ≅ BE.

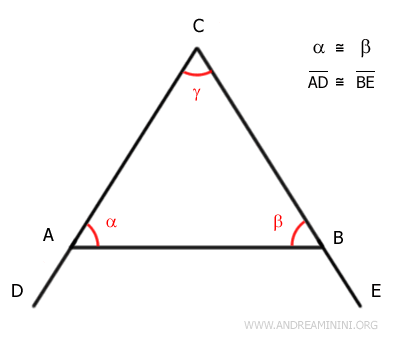
We introduce two new angles, α' and β'.

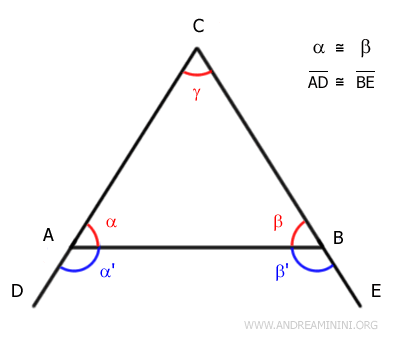
Since α and α' (and similarly, β and β') form a straight line, they are supplementary:

$$ \alpha + \alpha ' = 180° $$

$$ \beta + \beta ' = 180° $$

Solving for α' and β':

$$ \alpha ' = 180° - \alpha $$

$$ \beta ' = 180° - \beta $$

Since we assumed α ≅ β, it follows that α' and β' are also congruent.

$$ \alpha ' = \beta ' $$

Next, we connect A to E and B to D.

 

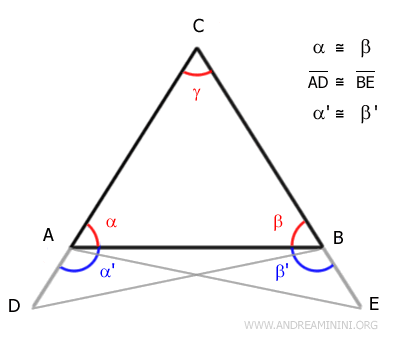
By the first congruence theorem, triangles ABD and ABE are congruent because they share a common side (AB), have congruent sides (AD ≅ BE), and congruent included angles (α' ≅ β').

$$ ABD \cong ABE $$

Since ABD and ABE are congruent, their corresponding sides and angles are also congruent.

In particular, we note:

$$ \overline{BD} = \overline{AE} $$

And the angles δ ≅ ε are also equal:

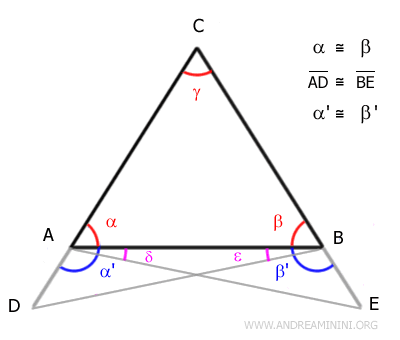
Similarly, θ ≅ σ:

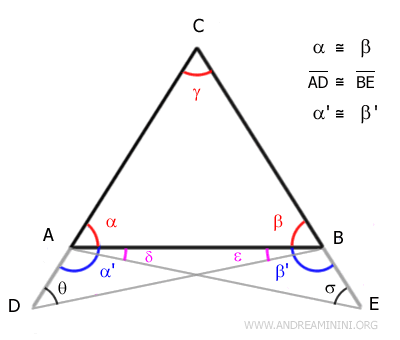
Since we established:

$$ \alpha \cong \beta $$

$$ \delta \cong \epsilon $$

We conclude:

$$ \alpha + \delta \cong \beta + \epsilon $$

By the second congruence theorem, triangles ACE and BCD must be congruent:

$$ ACE \cong BCD $$

Since ACE and BCD are congruent, their corresponding sides must also be congruent:

$$ \overline{AC} \cong \overline{BC} $$

This confirms that triangle ABC is isosceles since it has two equal sides.

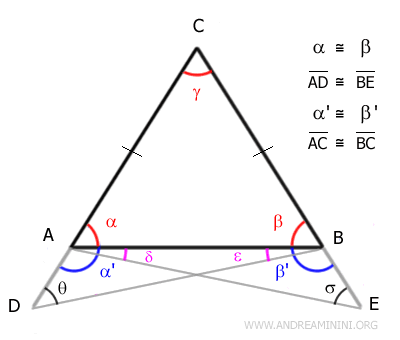
And that completes the proof. 

Alternative Proof

Let's consider a triangle where two angles are congruent, \( \alpha \cong \beta \).

Now, I draw the bisectors of angles \( \alpha \) and \( \beta \).

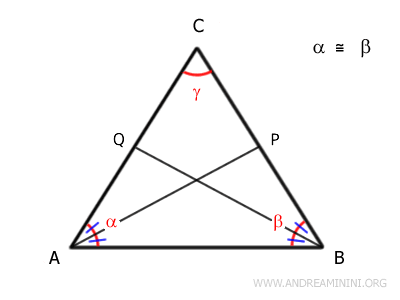
Since these angles are congruent, their halves must also be congruent:

\[ A\widehat{B}Q \cong C\widehat{B}Q \cong B\widehat{A}P \cong C\widehat{A}P \]

Triangles \( ABQ \) and \( ABP \) are congruent by the angle-side-angle (ASA) congruence theorem. They share side \( AB \) and have two pairs of congruent adjacent angles: \( \alpha \cong \beta \) and \( B\widehat{A}P \cong A\widehat{B}Q \).

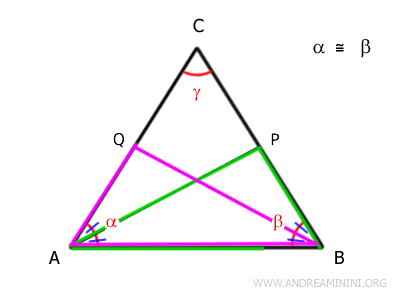
Since \( ABQ \cong ABP \), all corresponding sides and angles are equal, which gives us \( AP = BQ \) and \( A\widehat{Q}B = B\widehat{P}A \).

 

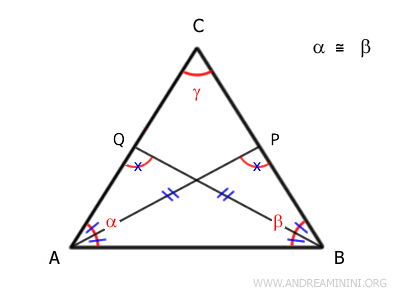
Because \( A\widehat{Q}B = B\widehat{P}A \), their supplementary angles must also be equal:

\[ C\widehat{P}A = C\widehat{Q}B \]

Now, let's examine triangles \( APC \) and \( BQC \).

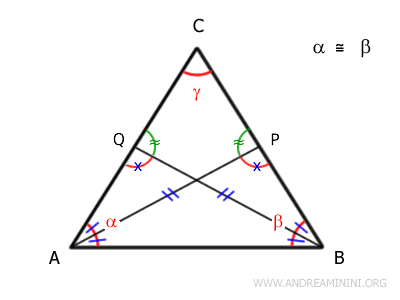
These triangles are congruent by the ASA theorem, since they have a pair of congruent sides, \( AP = BQ \) (already proven), and two pairs of congruent angles: \( C\widehat{A}P = C\widehat{B}Q \) and \( C\widehat{P}A = C\widehat{Q}B \).

Because \( APC \cong BQC \), all their corresponding sides and angles must be equal. In particular, we find:

\[ AC = BC \]

This confirms that triangle \( ABC \) is isosceles, as it has two congruent sides.

And that completes the proof.