Radius of an Inscribed Circle in a Triangle
The radius of a circle inscribed within a triangle is determined by dividing the triangle's area (A) by its semiperimeter (p). $$ r = \frac{A}{p} $$
This equation highlights a captivating link between the triangle's area, its perimeter, and the radius of the encircled inscribed circle.
It's a useful tool for tackling problems related to the characteristics of triangles and circles.
A Practical Example
Consider triangle ABC as our subject.
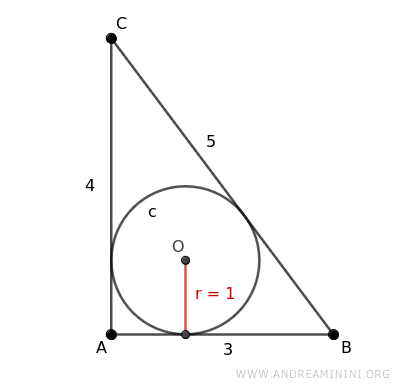
With the sides of the triangle measuring AB=3, AC=4, BC=5, and the radius of the inscribed circle being r=1.
Thus, the semiperimeter of triangle ABC is p=6.
$$ 2p = 3+4+5 $$
$$ 2p = 12 $$
$$ p = 6 $$
Calculating the triangle's area as A=6, I use the formula involving half the product of the base AB=3 and the height AC=4.
$$ Area_{ABC} = \frac{ \overline{AB} \cdot \overline{AC} }{2} $$
$$ Area_{ABC} = \frac{ 3 \cdot 4 }{2} = \frac{12}{2} = 6 $$
Now, let's find the ratio of the area A=6 to the semiperimeter p=6 of the triangle.
$$ r= \frac{Area_{ABC}}{p} = \frac{6}{6}=1 $$
This calculation reveals the length of the radius for the inscribed circle.
Note: For simplification, this example assumes a right triangle, but the principle is applicable across all triangle types.
The Proof
Consider any triangle, labeled ABC.
To locate the incenter - the heart of the inscribed circle - I draw the angle bisectors of triangle ABC.
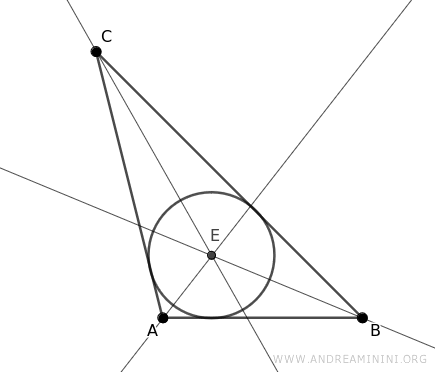
This inscribed circle touches each side of the triangle at points D, F, and G. As a result, segments EF, EG, and EH are the radii of the circle, all equal by definition: EF≅EG≅EH.
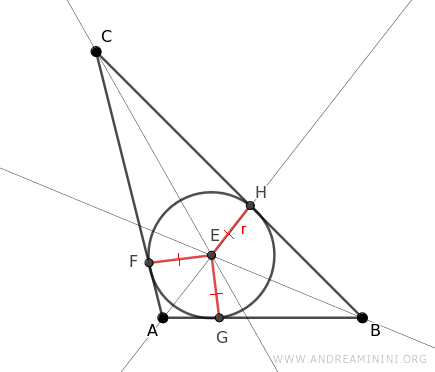
Moreover, these radii are perpendicular to the triangle’s sides where they touch, marking them as the heights of the sub-triangles ACE, ABE, and BCE within ABC.
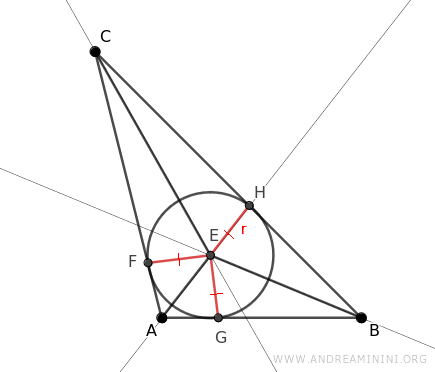
The areas of sub-triangles ACE, ABE, and BCE collectively equal the area of the larger triangle ABC, showcasing a beautiful symmetry. Thus, the aggregate of the areas of ACE, ABE, and BCE matches the area of ABC.
$$ \text{Area}_{ABC} = \text{Area}_{ACE} + \text{Area}_{ABE} + \text{Area}_{BCE} $$
Calculating the area of a triangle involves halving the product of its base and height. Here, for sub-triangles ACE, ABE, and BCE, the base is a side of ABC, and the height is the radius (r) of our inscribed circle.
$$ \text{Area}_{ABC} = \frac{ \overline{AC} \cdot r }{2} + \frac{ \overline{AB} \cdot r }{2} + \frac{ \overline{BC} \cdot r }{2} $$
Isolating the radius r:
$$ \text{Area}_{ABC} = r \cdot \left( \frac{ \overline{AC} }{2} + \frac{ \overline{AB} }{2} + \frac{ \overline{BC} }{2} \right) $$
$$ \text{Area}_{ABC} = r \cdot \left( \frac{ \overline{AC} + \overline{AB} + \overline{BC} }{2} \right) $$
The sum of the sides AC+AB+BC=P forms the perimeter (P) of triangle ABC, equivalently double its semiperimeter P=2p.
$$ \text{Area}_{ABC} = r \cdot \left( \frac{ 2p }{2} \right) $$
$$ \require{cancel} \text{Area}_{ABC} = r \cdot \left( \frac{ \cancel{2} p }{ \cancel{2} } \right) $$
$$ \text{Area}_{ABC} = r \cdot p $$
This elegantly proves that the area of triangle ABC equals the product of the inscribed circle's radius (r) and the triangle's semiperimeter (p).
And that's just the beginning.
